生態学のデータ解析 - GLMM 参照

• 混合 (効果) モデル，とくに一般化線形混合モデル (generalized linear mixed model; GLMM; 一般化線形混合効果モデルとも) を簡単に紹介するペイジです
  • 混合ではない一般化線形モデル (GLM) については GLM 参照 を
• 混合モデルは fixed effects と random effects の項を同時にもつ統計モデルです

  

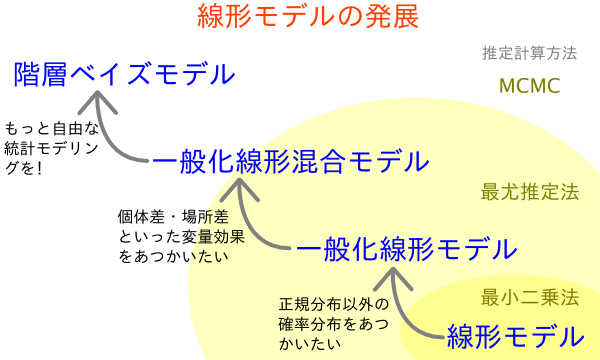
[もくじ]

• 2010 年代のニュース
• ネット上の GLMM の解説
• 混合モデルを推定計算する R の関数たち
  • 尤度を数値積分しようとする方法
  • MCMC 計算によって解決するもの
  • 尤度近似数値積分などつかう方法
  • 罰則つき擬似尤度 (PQL) つかう方法
• 正規分布の線形・非線型混合モデル
• もっと複雑な random effects をあつかいたい
• 書籍

2010 年代のニュース 

• 2017-10-26 glmmTMB
  • bioRxiv 論文 https://twitter.com/KuboBook/status/933585659347943425
  • メイリングリスト "AR(1) も?" https://twitter.com/KuboBook/status/933584598352650240

ネット上の GLMM の解説 

• 一般化線形混合モデル (GLMM) とは何か? -- 2006 年 3 月の生態学会新潟大会 データ解析自由集会 では「『個体差』のモデリング」として混合モデルをあつかっています
  • GLMM 解説記事 : 生態学会誌 (2006 年 9 月) に掲載
  • 数学セミナー2007: 数学セミナー (2007 年 11 月号) に掲載
• 沓掛展之さん による 動物行動学者のための一般化線形混合モデル では GLMM の自習の手がかりになる説明がなされています
• ベイズ統計 & MCMC もちょっとながめてみると良いかも
  • というのも GLMM は階層ベイズモデルを経験ベイズ法であつかっている，と見ることもできるので
• GLMM for ecologists and evolutionary biologists
  • そのFAQ
• GLMM 総説: Bolker et al. Generalized linear mixed models: a practical guide for ecology and evolution. Trends in Ecology & Evolution. doi:10.1016/j.tree.2008.10.008
  • 伊東さんによる紹介, tag/glmm

混合モデルを推定計算する R の関数たち 

• カウントデータ (ロジスティック回帰・ポアソン回帰で説明したいデータ) に random effects ある場合のモデル
• 久保要約:
  • random effects が一個だけ (``random intercept'' だけ) なら glmmML() in library(glmmML) がおススめ (glmmML 紹介)
  • もっと複雑な場合には
    • ベイズ統計 & MCMC (階層ベイズモデル + MCMC) や JAGS を使うべきでしょう
    • MCMCglmm も良いと思います
    • lmer() は何かと挙動不審で おススめできません
  • 伊東さんのまとめ: http://blog.so-net.ne.jp/ito-hi/2006-10-30-1

尤度を数値積分しようとする方法 

• 尤度を計算しているので AIC つかってモデル選択できる; あるいは尤度比検定もできる
• glmmML() (glmmML package): 「glmmML 紹介」も参照
  • random effects 切片 (intercept) をいれたモデルの推定計算ができる．
  • random effects は nest できない; 一個だけしか指定できない
• glm.nb() (VR package 中の library(MASS))
  • これは負の二項分布を family とする一般化線形モデルの最尤推定
  • 参照: glm.nb() 雑
• 他にもいろいろあるけれど，原理的には複数の random effects をもつ統計モデルにおいて，パラメーターを最尤推定することはかなり難しいので，MCMC によってパラメーターを推定する方法を検討するべきでしょう

MCMC 計算によって解決するもの 

• MCMCglmm() (MCMCglmm package): 「MCMCglmm」も参照
• 階層ベイズモデル化する → ベイズ統計 & MCMC

尤度近似数値積分などつかう方法 

• これらの方法はおススめではありません
  • 理由: 出力される推定計算結果があやしいので
• Laplace 近似によって計算された尤度はおそらく AIC によるモデル選択が可能
  • 「lmer 紹介」も参照

罰則つき擬似尤度 (PQL) つかう方法 

• これらの方法はおススめではありません
  • 理由: PQL つかった推定はあまり正確ではない; 尤度を計算していないので AIC つかってモデル選択できない; 尤度比検定もできない
• glmmPQL() (VR package 中の library(MASS))
  • 罰則つき擬似尤度 (penalized quasi likelihood, PQL) 法を使ってパラメーターを推定計算する
  • random effects を nest でき複数指定できる (下の library(nlme) 使っているので)
  • glm() と同じように family 指定できるらしい

正規分布の線形・非線型混合モデル 

• nlme() (nlme package)
  • method=ML とした場合 (default) は最尤推定法
  • 非線形モデルの推定計算もできる
• lmer() (lme4 package)
  • 上の GLMM 内の lmer() の説明参照
  • family=gaussian,method=ML とした場合は最尤推定法

もっと複雑な random effects をあつかいたい 

• ベイズ統計 & MCMC をみてください

書籍 

• Cawley. 2005. Statistics: An Introduction using R. Wiley (URL)
  • p.178 から random effects に関する丁寧な説明がある
    • その一部を訳してみた→ ランダム効果とは?
• Faraway. 2006. Extending the Linear Model With R: Generalized Linear, Mixed Effects and Nonparametric Regression Models (Texts in Statistical Science). CRC (URL)
  • Random Effects (chapter 8) などの解説にかなりペイジをとっている

    

• Youngjo Lee, John A. Nelder, Yudi Pawitan. 2006. Generalized Linear Models With Random Effects: Unified Analysis Via H-Likelihood. CRC. (URL)
  • 久保は持ってないのですけどよさそう

    

• McCulloh and Searle. 2000. Generalized, Linear, and Mixed Models. Wiley. (URL)
  • 久保は持ってないのですが表紙からしてよさそう

    

• 岡田昌史 (編). 2004. The R Book. 九天社. (URL)
  • 第 15 章「R でマルチレベルモデリング」 (林啓一) は線形混合モデルの解説である
• Pinheiro and Bates. 2000. Mixed-Effects Models in S and S-Plus. Springer. (URL)
  • 上記の nlme() 作者たちによる nlme 解説
• Venables and Ripley. 2002. Modern Applied Statistics with S (4th ed.). Springer. (URL)
  • 通称 MASS 本 (MASS4)
  • Chapter 7. Generalized Linear Models に上記の glm.nb(),glmmPQL() の解説がある
  • Chapter 10. Random and Mixed Effects に上記の nlme() の解説がある