生態学のデータ解析 - GLM 参照

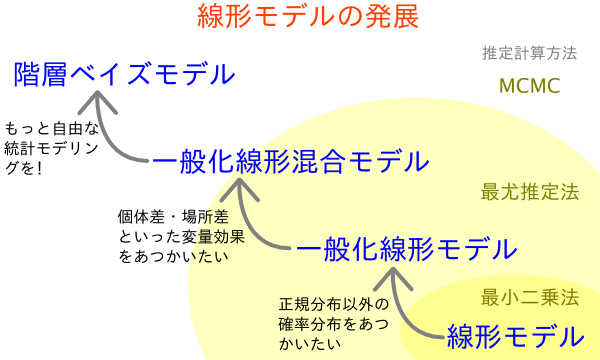
• 一般化線形モデル (generalized linear model; GLM) を簡単に紹介するペイジです
  • 一般化線形混合モデル (GLMM) については GLMM 参照
  • 一般化 (generalized) ではない一般線形モデル (general linear model) も GLM とよばれることがあります
    • 端的に言うと，一般線形モデル (正規分布モデル) は一般化線形モデル (他の分布も OK) の一部です

  

[もくじ]

• GLM の特徴
• ネット上の GLM の解説
• GLM を推定計算する R の関数
  • 雑
• 書籍

GLM の特徴 

• データのばらつきが二項分布やポアソン分布のときにも使える (その他，正規分布やガンマ分布の場合も)
  • 「世の中は何でもかんでも正規分布でいいんだ」といったまちがった考えかた (まちがった統計モデリング) から脱出するときに有用でしょう
• link 関数を指定することで説明変数 (要因) が応答変数に与える影響をさまざまに変えることができる (GLM link 関数)
  • これに対して，一般化 (generalized) ではない線形モデル (general linear model)では要因の影響は「足し算的」なものしかあつかえない

ネット上の GLM の解説 

• 一般化線形モデル (GLM) とは何か? -- 以下を参照してください
  • 久保 統計学授業
    • 統計学授業 2008 - ポアソン回帰・ロジスティック回帰の解説など
  • 生態学会大会 の「データ解析自由集会」
    • 2009 年 - GLM 再入門
    • 2004 年 - ポアソン回帰
    • 2003 年 - ロジスティック回帰・ポアソン回帰など
• 鳥屋にやさしい統計のお勉強
  • 鳥学会 2005 自由集会: わかりやすい GLM 説明あります
  • 鳥学会 2006 自由集会: 線形モデル，最尤法，モデル選択の解説

GLM を推定計算する R の関数 

• ずばり glm()
  • family については help(family) に詳しい説明あり
  • analysis of deviance は anova(glm(...), test = "Chisq")
    • anova() は generic な関数なので help(anova.glm) というふうにhelp を呼びだしてください
  • モデル選択 stepAIC() 関数も調べてみてください
  • まだ書きかけですが……FAQ 一般化線形モデル, 対数線形モデル, Gamma 分布の GLM
• データのばらつきが負の二項分布の場合: glm.nb()
  • これは 一般化線形混合モデル にちかい

雑 

• link 関数は自分で定義できるようだ (GLM link 関数)
• 一般化非線形モデル? 線形ではないモデルでポアソン回帰・ロジスティック回帰など
  • library(gnm)
    • 作者のペイジ -- なかなか詳しい解説あり
  • library(gnlm)
    • 作者 Lindsey さん のペイジに pacakge がおかれている (CRAN pacakge ではないので install.packages() が使えない)
    • いろいろな確率分布が使える

書籍 

• Agresti. 2003 (翻訳版). カテゴリカルデータ解析入門. サイエンティスト社 (URL)
  • さらに詳しい同著者の Categorical Data Analysis (URL) もあります
• Crawley. 2005. Statistics: An Introduction using R. Wiley (URL)
  • 第 13 章 ``Count Data'' その他に丁寧な説明あり

    

• Dobson. 2001. An Introduction to Generalized Linear Models (2nd ed.). CRC (URL)
  • GLM 入門書の古典
• Faraway. 2006. Extending the Linear Model With R: Generalized Linear, Mixed Effects and Nonparametric Regression Models (Texts in Statistical Science). CRC (URL)
  • いきなり GLM な本

    

• Venables and Ripley. 2002. Modern Applied Statistics with S (4th ed.). Springer. (URL)
  • 通称 MASS 本 (MASS4)
  • Chapter 7. Generalized Linear Models に上記の glm() の詳しい解説がある