生態学のデータ解析 - 最尤推定法とは

• 最尤推定 (さいゆうすいてい): 「最ももっともらしい」パラメーターの推定

  

• 「尤」の音読みは「ゆう」，訓読みは「もっともらしい (尤もらしい)」です．
• 尤度とは，ある確率論的モデルを仮定しているときに，その観測データが得られる確率 (あるいは確率密度)
  • 簡単には，ある観測データに (あるパラメーターのもとで) 確率論的モデルが「どれぐらいあてはまっているか」を確率で表す尺度です
• 最尤推定とは，尤度を「手持ちの観測データのもとで，あるパラメーター値が得られる確率」とみなして (つまり尤度が未知パラメーターの関数とみなして)，尤度を最大化するようなパラメーター値を探索する推定方法です
• 最尤推定法を使う手順は
  1. 尤度方程式を作る: 確率論的モデルを作り (データがどういう確率分布に従うか，確率分布のパラメーターの関数型はどうなってるか)，それを数式として定義する……これが尤度方程式である
  2. 尤度最大化によって最尤推定値を計算する: そのモデルで定義される「尤度 (ゆうど)」を最大化させるパラメーター推定値を計算する……これが最尤推定値 (maximum likelihood estimate; MLE)

  別のいいかたをすると，確率論的モデルのパラメーターを変えていって，観測データにもっともよく「あてはまる」ところを探索していく方法です．

• 実際の計算では尤度ではなく対数尤度を最大化して最尤推定値を計算します．これはそのほうが計算が格段に簡単になるためです．
• 最小二乗法との関係: 統計モデルの確率分布が (等分散) 正規分布であるとき，最小二乗法の推定量は最尤推定量は一致します

簡単な例

• あるモデル: コインを投げたときにオモテがでる確率は p = 0.6 である (と仮定している)
• 観測データ: 10 枚のコインを投げたら 7 枚がオモテだった
• 尤度 (二項分布の計算):
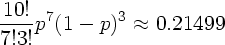
• 最尤推定: p = 0.6 は観測された現象を説明できる良いモデルなのだろうか?
  • 尤度を最大化する p を計算したい
  • この例だと尤度を最大化するのは p = 0.7

解説とか

• 2008 年 11 月の 統計学授業 2008 の 2 回目でごく簡単な事例について説明してます．
• 2006 年 1 月の 統計学授業 の 3 回目でごく簡単な事例について説明してます．
• 2005 年 3 月の 生態学会大会 の自由集会 の前口上で最尤推定法のごく簡単な説明してます．

最尤推定と R

• もっとも簡単に最尤推定を行うには free な統計ソフトウェア R を使うのがよいでしょう (R 関連の参照)
• R で使える最尤推定法の関数の一部
  • glm() : 一般化線形モデルを計算する関数
    • logistic 回帰や Poisson 回帰などが簡単にできる
    • GLM 参照
  • nlme() や nls() など: 等分散正規分布を仮定している線形・非線型の混合モデルを最尤推定法
  • optim(): 究極のわざ，自分で定義した尤度関数を最大化できる

• 古い内容
• 「父親として成功するシウリザクラの条件」を最尤推定する方法の 解説メモ (PDF, 57KB) 2003 年度の計算}
• KKPA: 個体ごとに観測期間がばらばらな場合の (一定速度) 死亡率推定法の Perl スクリプト
• 確率論的死亡モデル (二項分布と logistic な関数型を仮定) のパラメーターを最尤推定する方法のすごく初歩的な 解説 (PDF ファイル, 2000.12.08 更新)