生態学のデータ解析 - lmer MCMC 計算

• cf. lmer 紹介, GLMM 参照, ベイズ統計 & MCMC, coda 雑
• R の help: mcmcsamp(), lmer()
• ここは lmer() (in library(lme4)) が生成する線形混合モデル (lmer)・一般化線形混合モデル (glmer) オブジェクトを階層ベイズモデルとみなして，その MCMC 計算する関数 mcmcsamp() (同じく library(lme4)) の説明です．
• 現時点の久保の理解: つまり線形混合モデル・一般化線形混合モデルの階層ベイズモデルの MCMC 計算は R2WinBUGS など使わずとも lmer() と mcmcsamp() 使えばできるらしい (もちろん複数の random effects をあつかえる)．
  • fixed effects の事前分布は一様分布 (局所的無情報事前分布)
  • random effects の事前分布は (おそらく) 平均ゼロの多変量正規分布で，その分散共分散行列の超事前分布は (逆) Wishart 分布

とりあえず，の例題

library(lme4) の lmer() 関数に一般化線形混合モデルの問題を解かせると

fit1 <- lmer(y ~ (1 | group), family = binomial, method = "Laplace", ...)

glmer オブジェクト fit1 が作られる． これを summary(fit1) すると……

Generalized linear mixed model fit using Laplace 
Formula: y ~ (1 | group) 
 Family: binomial(logit link)
  AIC  BIC logLik deviance
 1385 1395   -690     1381
Random effects:
 Groups Name        Variance Std.Dev.
 group  (Intercept) 0.0353   0.188   
number of obs: 1000, groups: group, 10

Estimated scale (compare to  1 )  0.9976 

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)    0.108      0.087    1.24     0.22

次に glmer オブジェクト fit1 を mcmcsamp() 関数に渡すと

mcmc1 <- mcmcsamp(fit1, n = 500) # library(coda) の mcmc オブジェクト

mcmc オブジェクト mcmc1 が作られるので

• 注: lme4 version 0.999375-31 の場合，mcmc オブジェクトではない

(注: library(coda) も忘れず実行してから) summary(mcmc1) を実行すると

• 注: lme4 version 0.999375-31 の場合，summary(as.mcmc(as.matrix(mcmc1))) とする必要がある?!

Iterations = 1:500
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 500 

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

                   Mean     SD Naive SE Time-series SE
(Intercept)       0.109 0.0999  0.00447        0.00528
log(grop.(In))   -3.391 1.1070  0.04951        0.14390
deviance       1385.842 6.2637  0.28012        0.47325

2. Quantiles for each variable:

                   2.5%       25%      50%      75%    97.5%
(Intercept)      -0.084    0.0474    0.104    0.169    0.318
log(grop.(In))   -6.022   -3.9808   -3.269   -2.629   -1.521
deviance       1375.724 1381.4101 1385.200 1389.406 1399.566

• MCMC 計算の結果に含まれてる log(grop.(In)) は group の random effects (つまり group 差) あらわす 事後分布の分散の log になっている
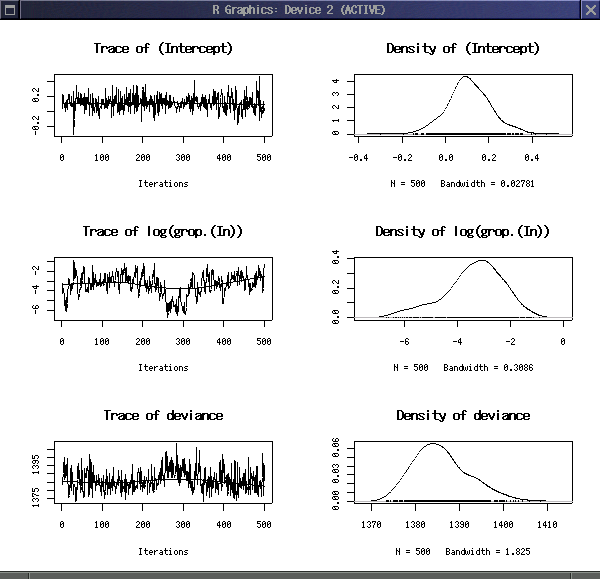
• plot(mcmc1) するといつものごとくこういう図になる
  • 注: lme4 version 0.999375-31 の場合，plot(as.mcmc(as.matrix(mcmc1))) とする必要がある?!
    • xyplot(mcmc1) だの densityplot(mcmc1) でよい，とわかりました