

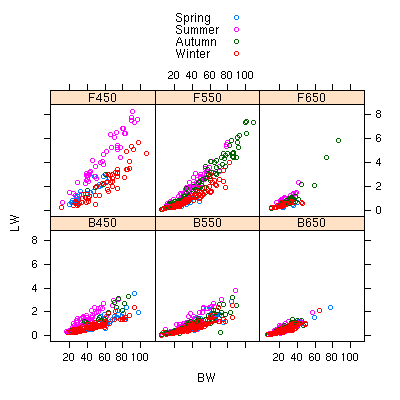
lmer()
はダメっぽい
(推定値はそれっぽいけど,
AIC の計算とかで何をやっているのかよくわからない),
ということでまたゐんばぐすをもちだすことに.
lmer()
をひねくってみたのだけど,
いろいろと仕様なんかもかわり
(こういうのを頻繁変えてしまうのが Douglas Bates のぽりしー?),
また数値的な最尤推定計算も Laplace 近似ではなく
Gauss-Hermite 近似が default になっていた
(nAGQ = 1 にすると Laplace 近似)
……
近似計算の精度 nAGQ オプションの指定,
これに deviance の推定値などは依存している部分があるように見える.
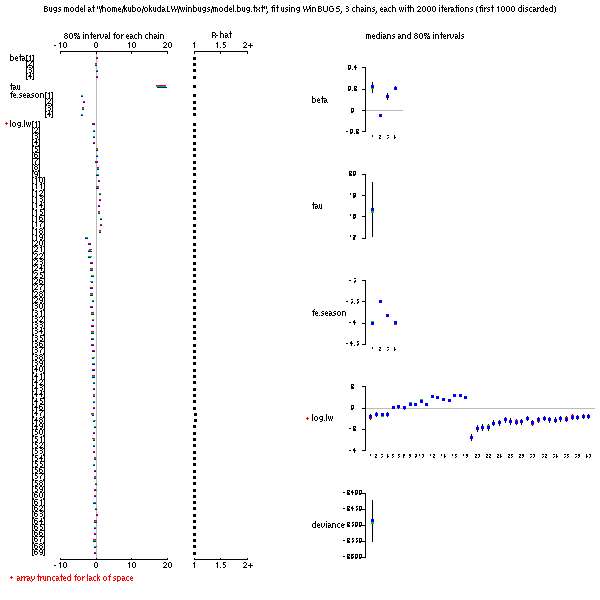
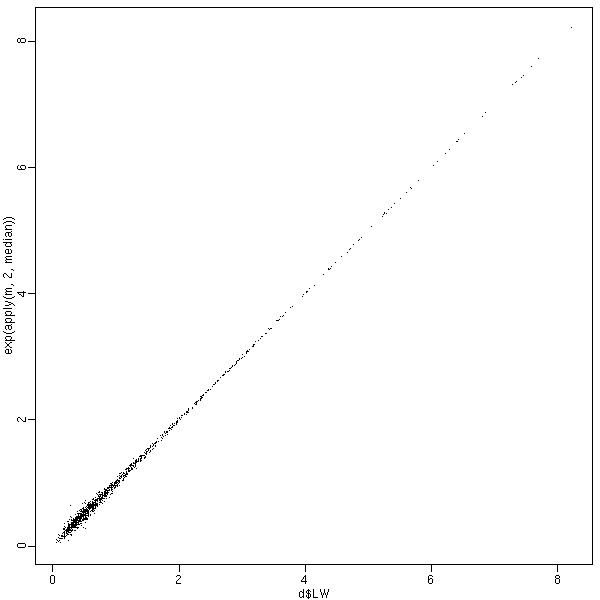
lmer()
相談のつづき.
仕様がやたらとかわる lmer()
……
本日解明できた重要な性質としては,
現状最新版ではいまだに Gauss-Hermite 近似
(nAGQ を 2 以上に指定)
による積分尤度はマトモに計算できず,
依然として
Laplace 近似を使うしかない
(nAGQ = 1).
nAGQ = 1)
の場合はこんなかんぢなのだが,
Generalized linear mixed model fit by the Laplace approximation Formula: f Data: d AIC BIC logLik deviance 166 212 -73.8 148 Random effects: Groups Name Variance Std.Dev. ID (Intercept) 0.000 0.00 Residual 0.109 0.33 Number of obs: 1353, groups: ID, 1353 Fixed effects: Estimate Std. Error t value (Intercept) -4.777170 0.097535 -49.0 SeasonSummer 0.591766 0.025425 23.3 SeasonAutumn 0.338857 0.027257 12.4 SeasonWinter -0.051675 0.027241 -1.9 AreaSouthern 0.583936 0.014148 41.3 Depth -0.001259 0.000117 -10.7 SL 0.011122 0.000430 25.9Gauss-Hermite 近似 (
nAGQ = 10, ただし分割点数とはあまり関係ない)
ではこうなった.
Generalized linear mixed model fit by the adaptive Gaussian Hermite approximation Formula: f Data: d AIC BIC logLik deviance 1920 1966 -951 1902 Random effects: Groups Name Variance Std.Dev. ID (Intercept) 7.40 2.72 Residual 2.78 1.67 Number of obs: 1353, groups: ID, 1353 Fixed effects: Estimate Std. Error t value (Intercept) -4.78e+00 2.84e+15 -1.70e-15 SeasonSummer 5.91e-01 7.03e+14 8.00e-16 SeasonAutumn 3.39e-01 7.22e+14 5.00e-16 SeasonWinter -5.23e-02 6.78e+14 -1.00e-16 AreaSouthern 5.83e-01 4.32e+14 1.40e-15 Depth -9.82e-01 3.30e+12 -2.97e-13 SL -1.85e-01 1.23e+13 -1.51e-14係数の推定値の
Std. Error
の異常なる値をみてやってください.
ついでにいうと,
じつは推定値自体もけっこうヘンだったり.
lmer()
っていつまでたってもアヤしいままなんでしょうねえ
……
しかしながら,
lmer()
を使うしかない,
といった状況だと思う.
であるならば,
これからもしばらくは Laplace 近似な推定計算をするほかない.
glmmML()
で推定計算すればよいだろう.
これも近年は Laplace 近似が default
の最尤推定計算方法になってしまったけれど,
Gauss-Hermite 近似でも,
まあそんなにヘンな結果にはならない
……
私が調べた範囲では G-H 近似のほうが「少しマシ」な推定値になってた.




table()
や
xtab
は集計に便利な関数だけど,
複雑な場合には ftable()
や stat.table() in library(Epi)
を使う
y ~ x1 + x2
みたいな記法は Wilkinson-Rogers formulas
とよばれる (もともとの WR は y = x1 + x2
a:(b + c) = a:b + a:c
transform()
ordered
型が等間隔な選点直交多項式となってるのは歴史的理由?
drop = FALSE
を指定 (第 3 要素指定で!)
class() と typeof()
を同一視していたけど,
これはまちがい: R には型とクラスの両方ある
env$object
だけでなく
env[["name"]]
でもある環境内のオブジェクトにアクセスできる,
と質問してみてわかった
apply()
や
tapply()
が好きだけど,
with()
や by()
のほうが記法的にはすっきりしてる場合もある
……
f <- function(xx)
は f(x = 1) と呼べてしまう!
(危険なだけで利点がないような)
deparse(substitute(式))
str() で double 型が
num となるのは歴史的理由
library(dichromat)
(RGM)
で調べられる
(bluscale() といった関数も含まれる)
hexbin()
(これは CRAN ではなく Bioconductor に含まれる)
を使う: 六角形の desnity plot に変換される
png(), pdf()
その他いくつかに限定される)
library(ggplot2)
の紹介:
library(lattice)
の対抗馬,
つまりもうひとつの
library(grid)
世界の高水準作図関数セット
library(ggplot2)
の独特な記法:
time <- ggplot(data, aes(x = Date, y = Ozone)) print(time + geom_point() + geom_smooth())…… といったかんじで
+ 演算子で重ね描き・
グループごとの分割などを指定する
library(ggplot2)
は Lee Wilkinson の本 ``The Grammar of Graphics''
(グラフの分類学の本だそーで)
にもとづくもので,
Hadley Wickham が実装している
library(ggplot2)
で作れる図って
library(lattice)
(あるいは coplot() とか)
でも作れるのでは?
とすると
library(ggplot2)
の advantage は?
……
と質問してみたら,
まあそのあたりその二つを比較して,
こっちが優れてるとか判断するのは簡単ではないけど,
まあそれぞれに使っていくうちにユーザーが判断していくしかないんでは,
といった内容の回答でした
prompt()
や promptPackage()
などなどといった関数でスケルトンを生成できる
R CMD check MyPackage
とするとありがちなまちがいなどをチェックしてくれる
export(),
import() で package 内
関数が「外」から見える・見えないの設定
.C()
とかは単純だけど
.Call()
なんかを使ったほうがいいよ,
とのご教示
#include <Rinternals.h>
すると S 言語オブジェクト一般をあつかう型
SEXP
が使えるようになる
LENGTH(),
pointer をとる INTGER() & REAL(),
要素をとりだす VECTOR_ELT(),
その他文字列関連あれこれ,
「なんでも vector」
な R SEXP をスカラー化する関数,
C 言語の世界で R オブジェクトを生成する
allocVector()
& mkString(),
メモリ管理 (ガベジコレクション対策)
PROTECT()
& UNPROTECT()
その他あれこれ,
さらには R クラスの attributes
を操作する関数あれこれ,
……
#include <Rdefines.h>
を使うと
S4 クラスを C 言語内で生成したり操作できる
pairlist() で定義できる)
……
これの使いみちがいまいちよくわからなかったんだけど
(あえて言えば name つき vector の代替物?),
何やら自分で parser & evaluator 利用する場合に関係ありそう
……
R -d gdb foo.R
でいいよ,
とのこと
……
これは便利だ!
(swig 的だ
……
ぎょーむ日誌 2006-02-24)
