ssh 二段重ねわざで安直に)
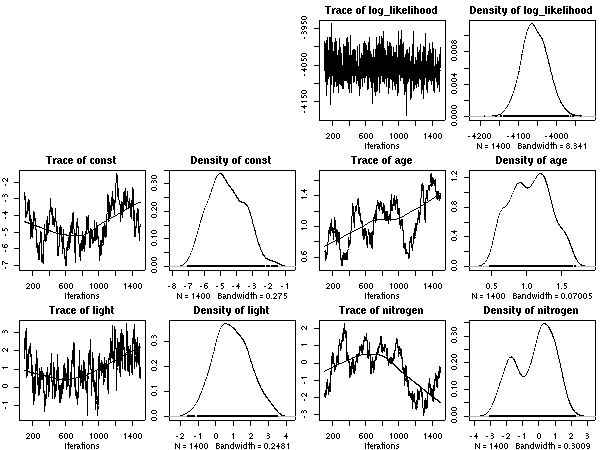
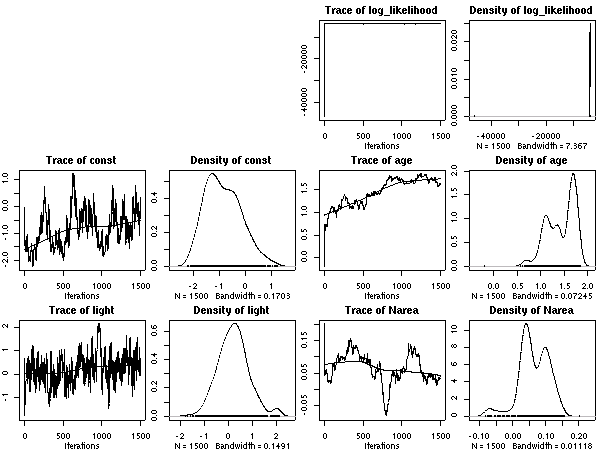
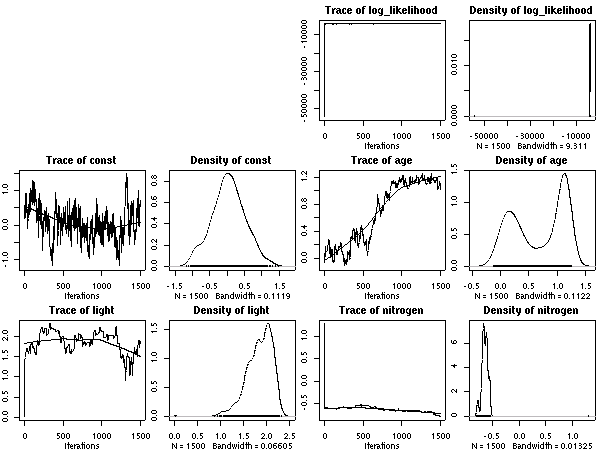
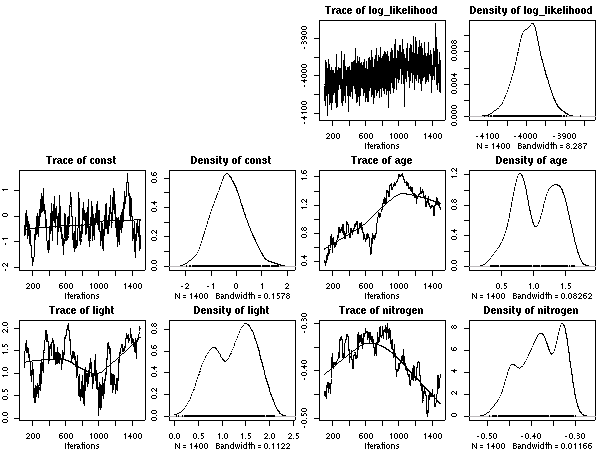
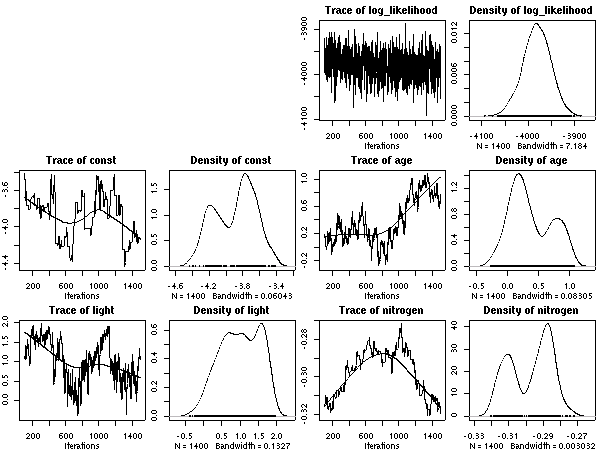
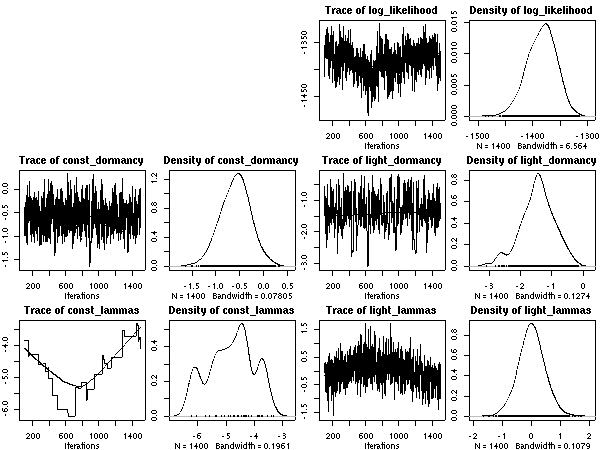
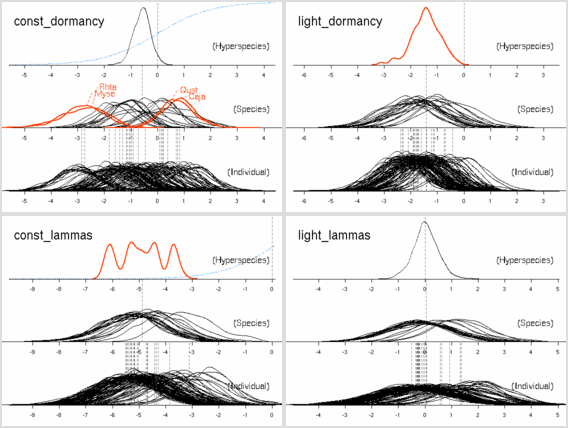
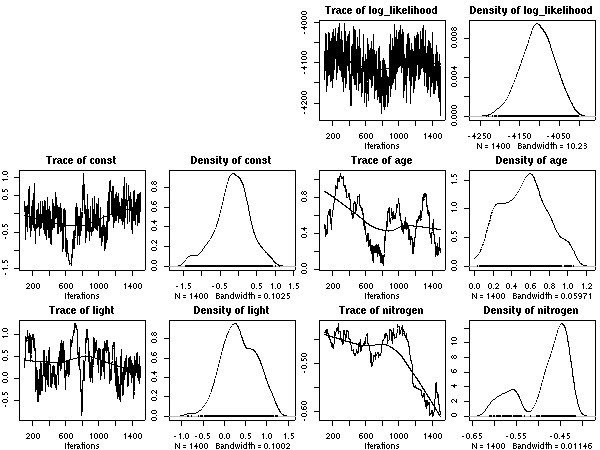
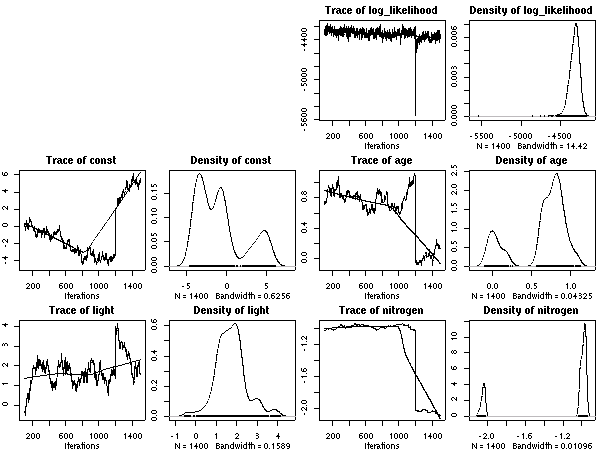
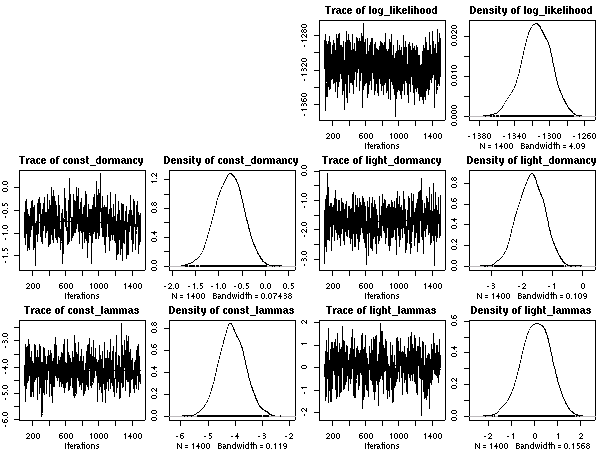
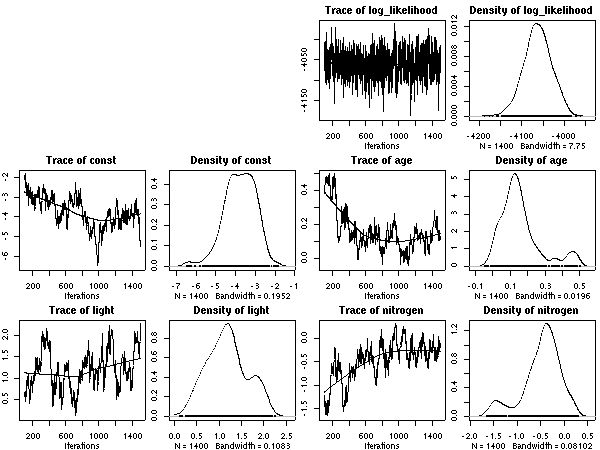
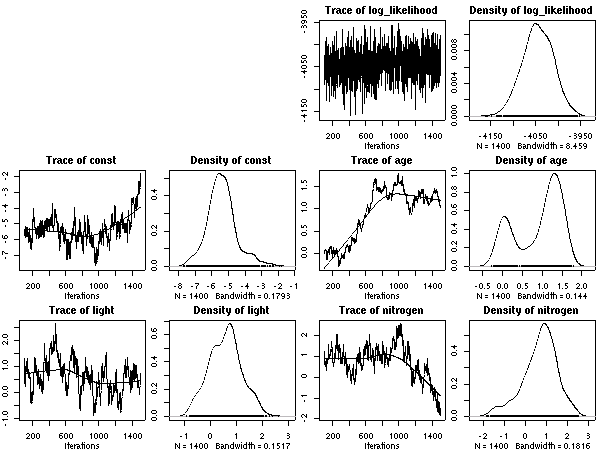
計算経過をのぞいてみると
……
まあ，
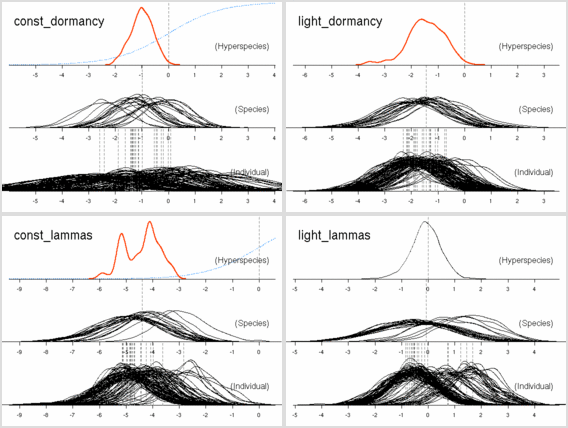
こちらのほうが (N_mass 版より) 尤度高めで，
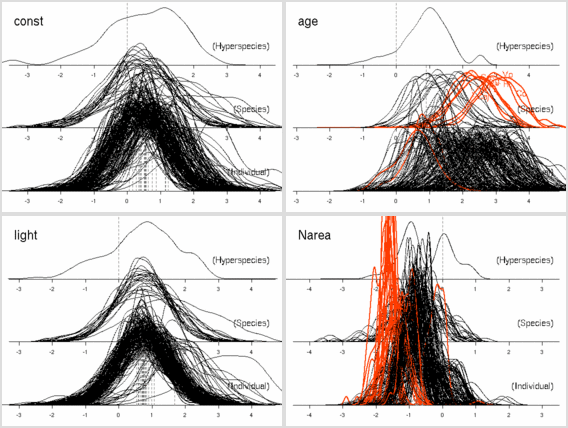
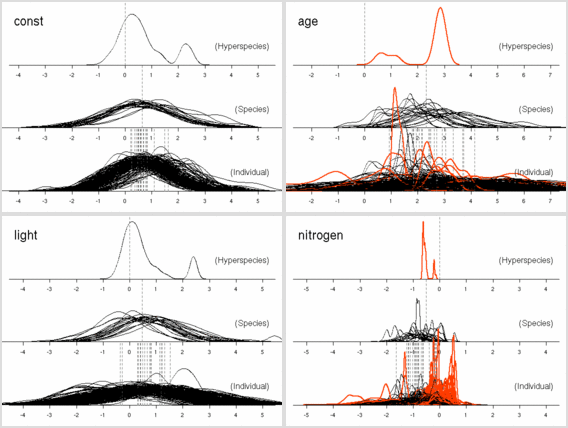
窒素はほとんど効果ナシ
(休眠・二度伸びで枝を「揺らしてやる」効果あるのか，
以前よりは N_area パラメーターは多少は振動するようになっている)．
明るいと短命，
という妥当な効果あると思うんだけど，
事後分布の分散は (上と同じく) 大きな値になりそう．
たぶん，
ここでも葉齢パラメーターの「個体差」のばらつきがでかいはず．
unused
指定できるようにはしてるんだけど，
これってあまりちゃんとしてないんだよね．
実験的に値をゼロに固定して計算させて様子をみる，
というような目的のためのものなんで．
尤度まわりとかもきちんと設定，
などなど．
current: 0 0 0 0 0 0 try: 1 0 0 0 0 0 --> REJECT! current: 0 0 0 0 0 0 try: 0 -1 0 0 0 0 --> ACCEPT! current: 0 -1 0 0 0 0 try: 0 -1 0 0 0 -1 --> REJECT! current: 0 -1 0 0 0 0 try: 0 -1 0 0 0 1 --> REJECT! current: 0 -1 0 0 0 0 try: 0 -1 0 0 1 0 --> REJECT! current: 0 -1 0 0 0 0 try: 0 -1 0 0 1 0 --> ACCEPT! (... 中略 ...) current: 0 -1 0 0 2 2 try: 0 -1 0 0 3 2 --> ACCEPT! current: 0 -1 0 0 3 2 try: 0 -1 0 -1 3 2 --> REJECT! current: 0 -1 0 0 3 2 try: 0 -1 0 0 2 2 --> ACCEPT! current: 0 -1 0 0 2 2 try: 0 -1 0 0 2 3 (... 後略 ...)
1 + age + light + nitrogen
から
1 + (1 + light) * age + nitrogen
というふうに
(一年間 の死亡確率が logistic
式で与えられてれるモデル)．
ここ数日の結果から考えて，
たぶんこれがより良いモデルになっているはず．
計算開始．
今回は 100 MCMC step とばしではなく，
50 MCMC step とばしで．
とりあえずは．
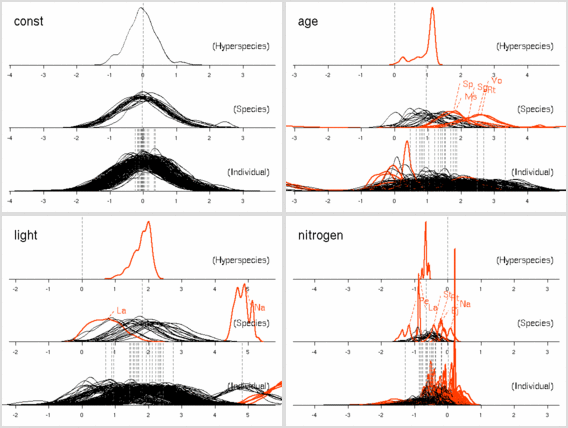
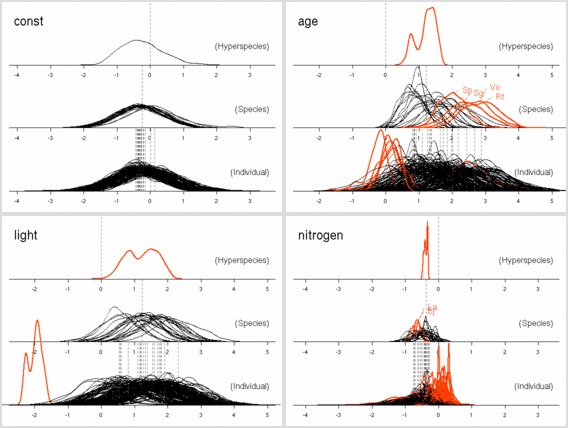
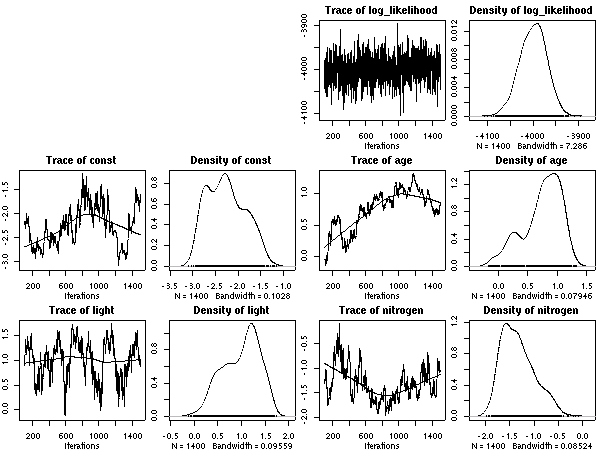
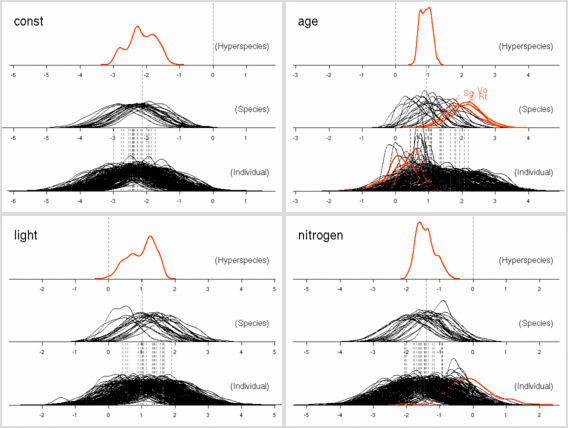
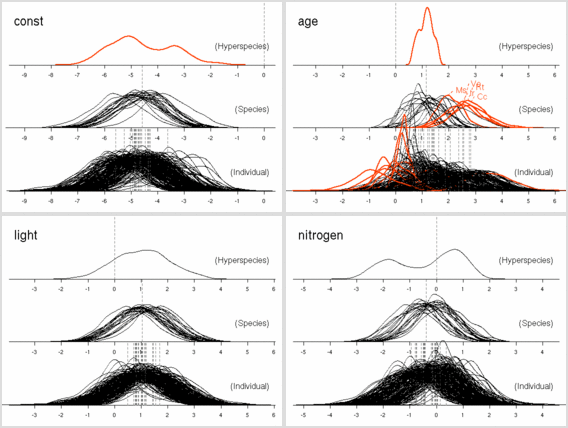
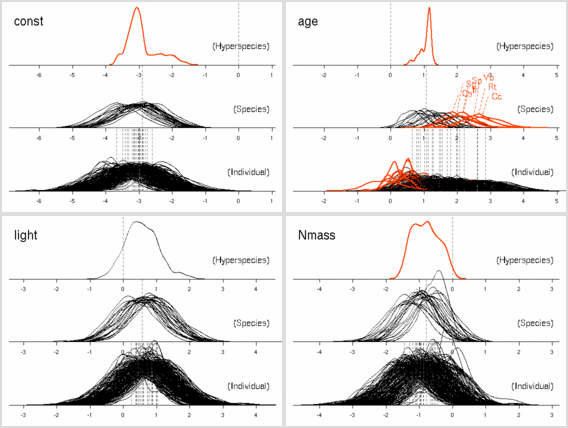
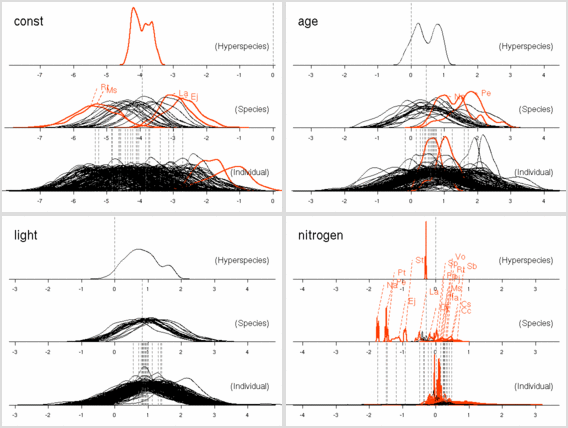
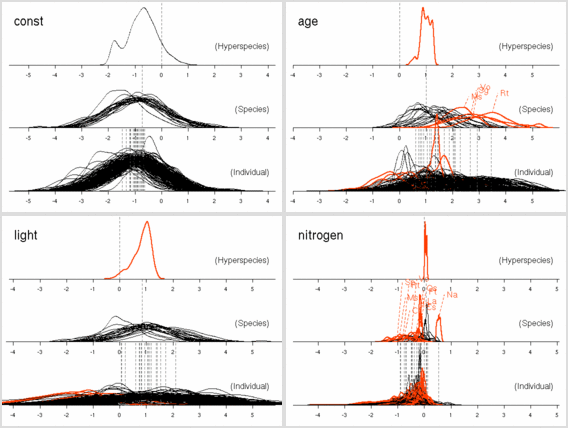
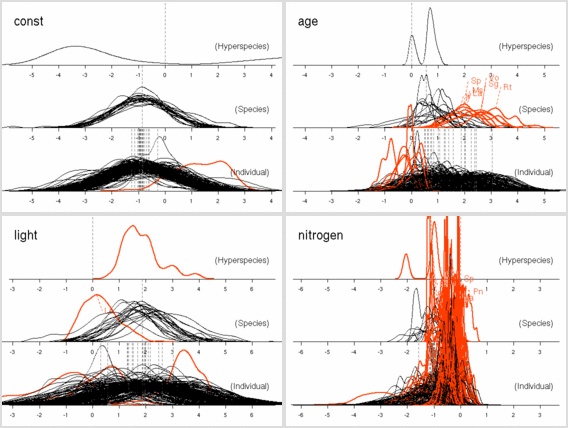
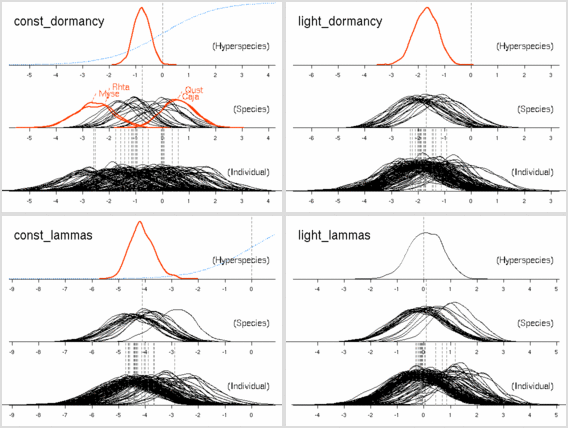
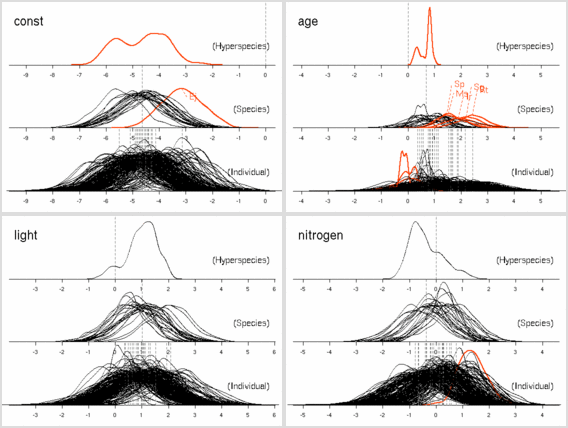
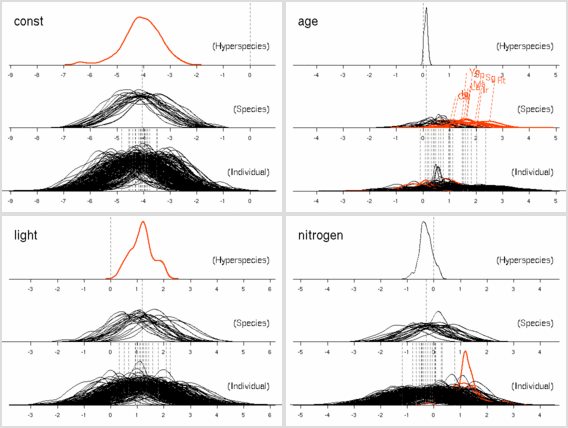
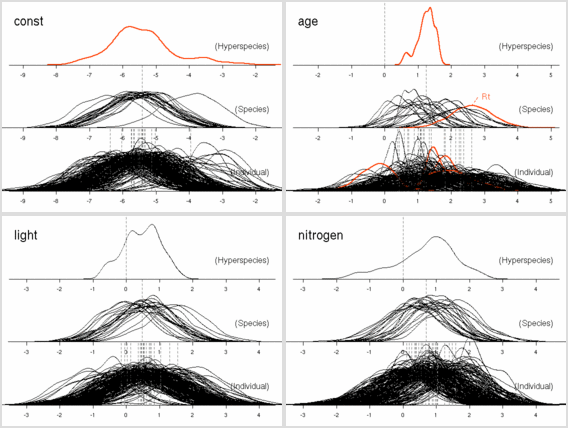
age
パラメーターにおいても
「ちょっとふつーとは違うぜ」の樹種たちがいる．
これは葉っぱ脱落の状況をみると，
明るいところでも暗いところでも葉っぱがどんどん早死にしてる
(3 年ぐらいしかもたない)
連中，
とわかった．
$hyperspecies
を一個ではなく二個準備してやって，
片方では (メトロポリス用の) 「温度」を上げてやって，
あとは「てきとー」に入れ換えていくだけ，
だよね．
パラメーター
α
の事前分布を
としたときに，
と変化する確率を
なんかで下のように「規格化」
(というか条件つけというか)
してやらねばならない．
といった独立サンプラー (independence sampler)
で生成され，
さらにその関数型が事前分布と同じ，
つまり
であるなら，
と変化する確率は
などがよけーなのである．
二重に
を勘定してることになるのかな．
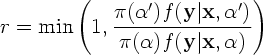
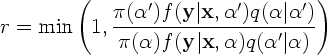
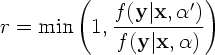
-1, 0, 1, 2, 3, ...
/var/log/maillog
なんかにも
Jan 4 21:06:38 hosho qmail: 1136376398.511651 delivery 148: success: Incorrectly_built_binary_which_accesses_errno_or_h_errno_directly. _Needs_to_be_fixed./Incorrectly_built_binary_which_accesses_errno_or_h_errno_directly. _Needs_to_be_fixed./Incorrectly_built_binary_which_accesses_errno_or_h_errno_directly. _Needs_to_be_fixed./did_0+0+2/といった呪詛でうめつくされているんで．
qmail を 5 年ぶりぐらいに再構築．
とどこおっていたメイル配信が再開された．
error.h
の
extern int errno;
を
#include <errno.h>
と変更してまた再構築 (といっても 10 秒ぐらいで終わるんだが)．
どうやら，
これでひとまず問題解決したもよう．
hosho
にアカウント作ってほしいとの依頼あったんで，
作業してると
……
なんか adduer
したのにアカウントできないな?
といぶかしく思ってるうちに HDD くらっしゅ．
どうしてこのタイミングで壊れるのかね．
e2fsck．
非力なマシン (Duron 0.8GHz) に大きめの HDD つんでるので，
チェック・修復に時間かかる．
もし HDD の円盤が物理的にコワれてたら修復しようがないんだが
……
hosho
のトンネル使ってた雪野さんからも
……
scale = 3.0
(つまり IG(1, 3))．
事後分布描画の標本範囲は 501:1500．
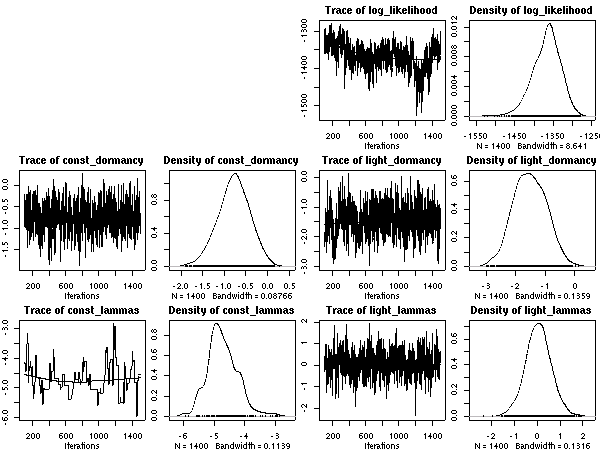
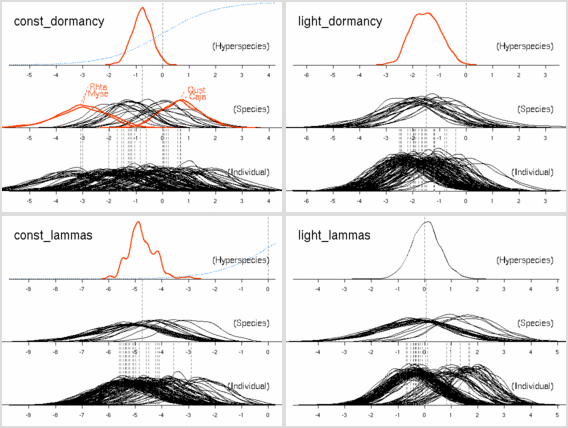
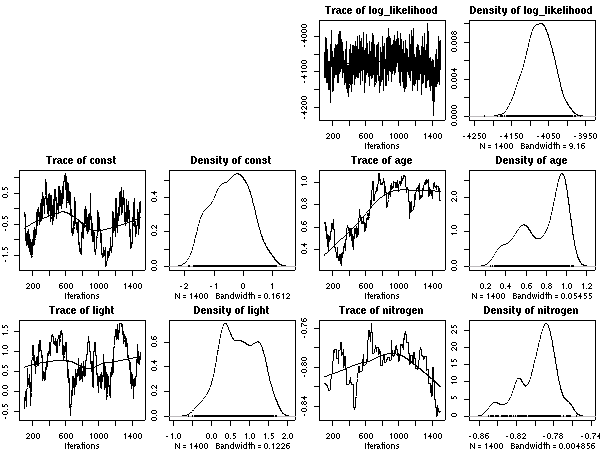
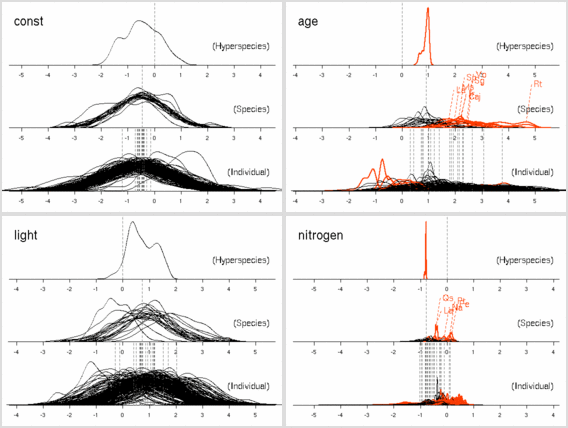
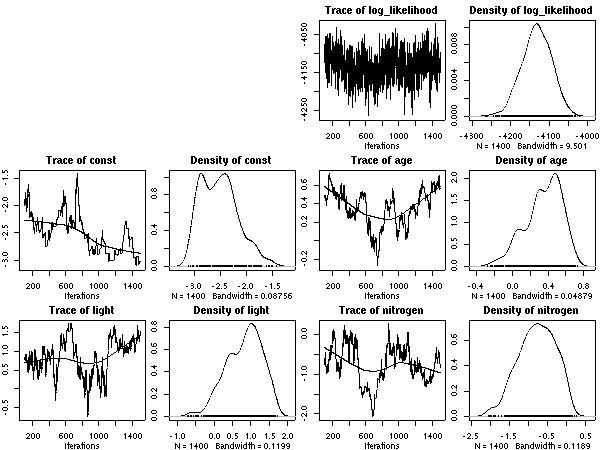
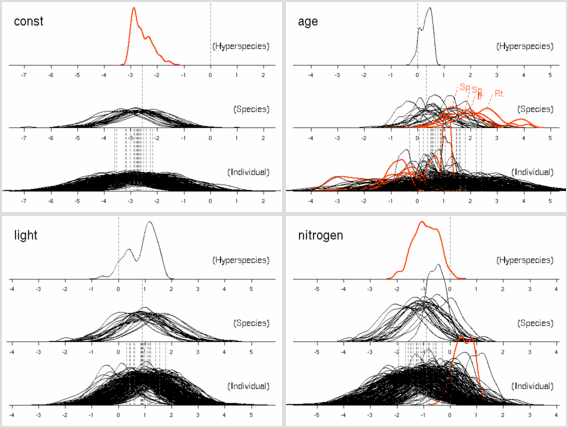
scale = 1
とかダメっぽいような気がする．
個体差とかが無意味にでかくなる．
scale = 20
とかにしてみる
(上で示してる計算結果では
scale = 3)．
scale = 20
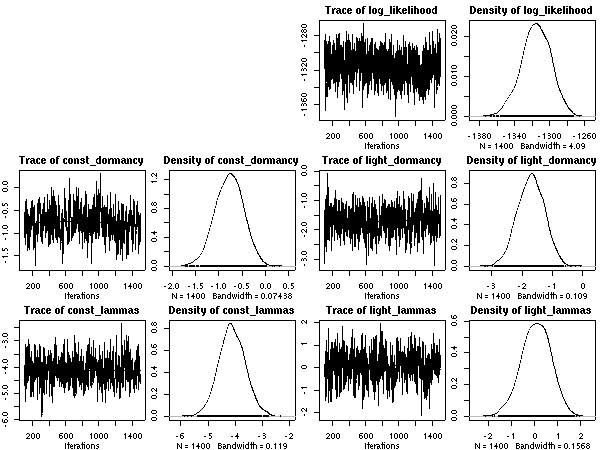
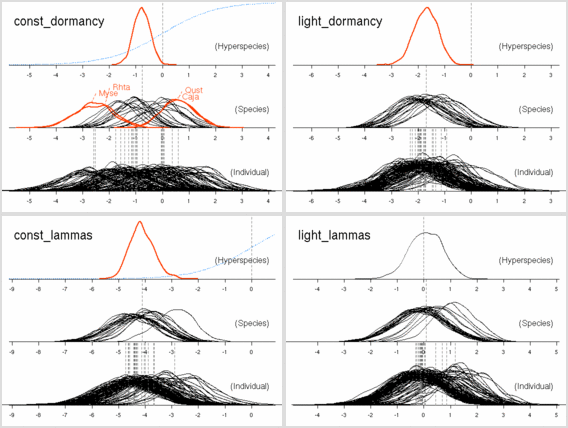
とした休眠・二度伸び計算やりなおしが終了．
幸か不幸か，
超事前分布のパラメーターを変えたぐらいでは結果はほとんど同じ．
「多峰」状態は多少マシか?
マシになったのがいいことなのかマズいのかよくわからんけど．
よくわからぬまま，
この結果を使って葉っぱ生き死に確率の推定計算もやらせる．
あいかわらず試験運転的な 50 MCMC step とばしのサンプリング．
scale = 20
とした試験運転的計算
(つまり
50 MCMC stepとばしサンプリング
……
MCMC バグをかたづけてからはこれぐらいの間隔で十分というかんぢ)，
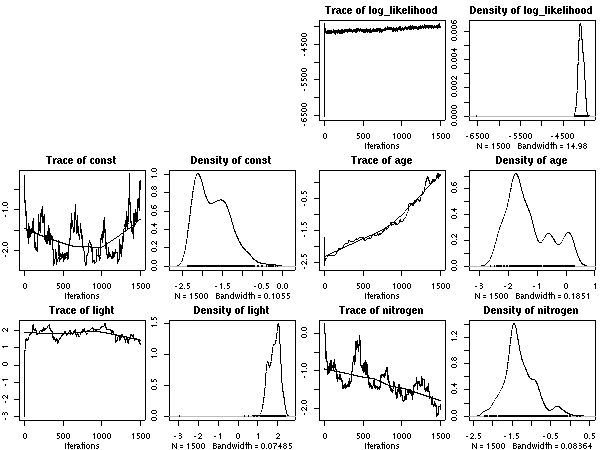
葉重量窒素濃度モデルに関しては終了．
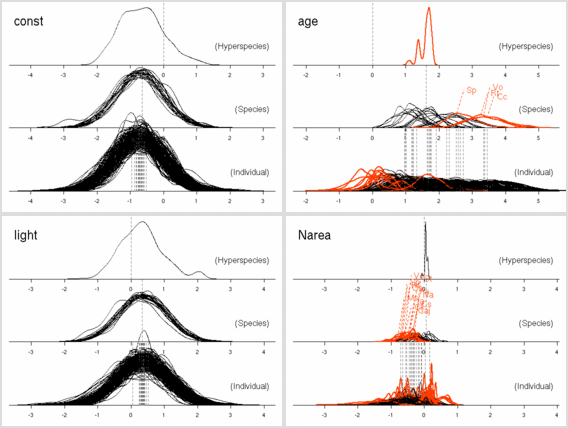
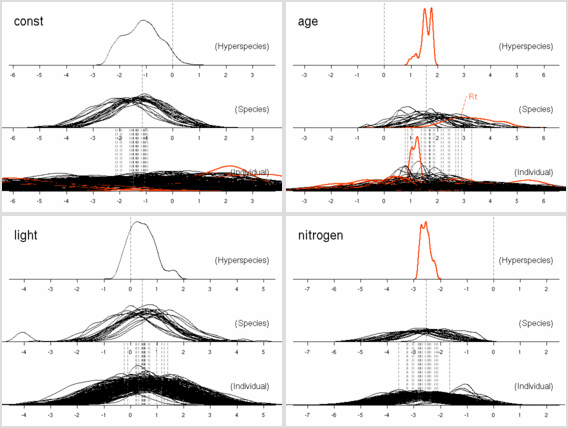
まあ，
あまりかわりばえしない．
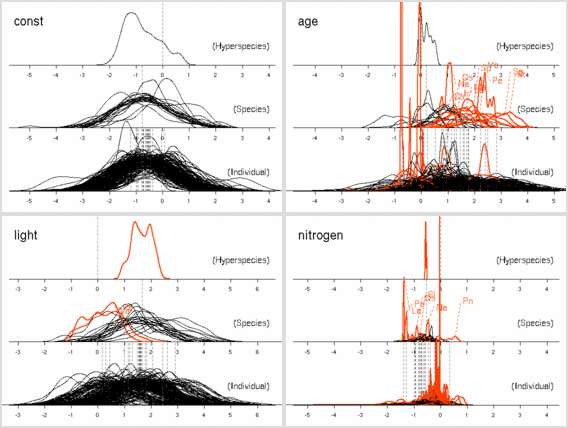
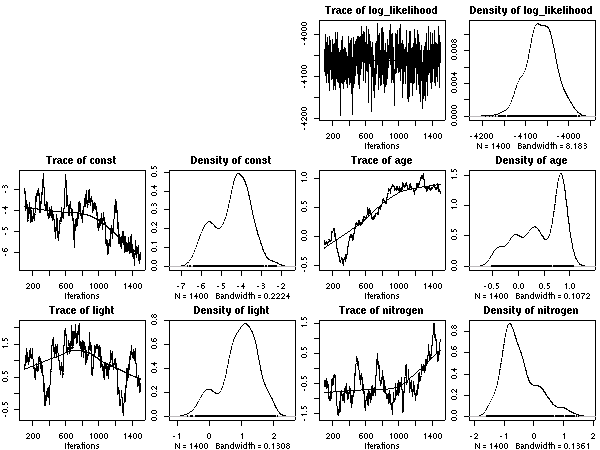
あいかわらず窒素が多いと長命化
……
ということで，
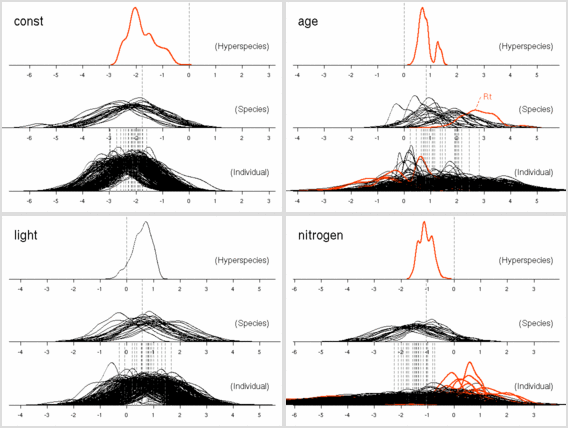
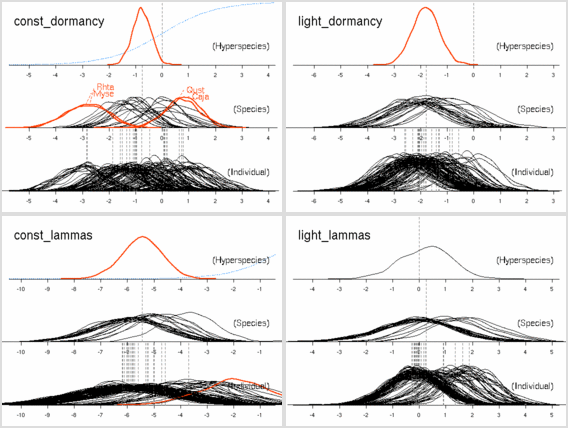
元データから次のような図を作ってみる．
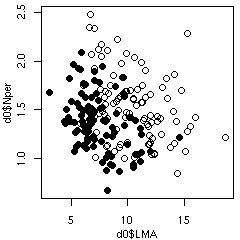
後記: ここは記述がまちがっていて (さいわいにも計算プログラム内ではまちがっていなかったんだけど)， Narea = Nmass * LMA が正しい． つまり， Narea なる量は LMA とほぼ同じ， ということ．
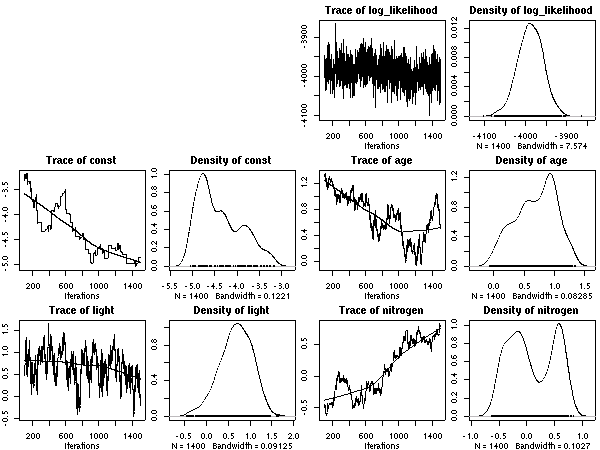
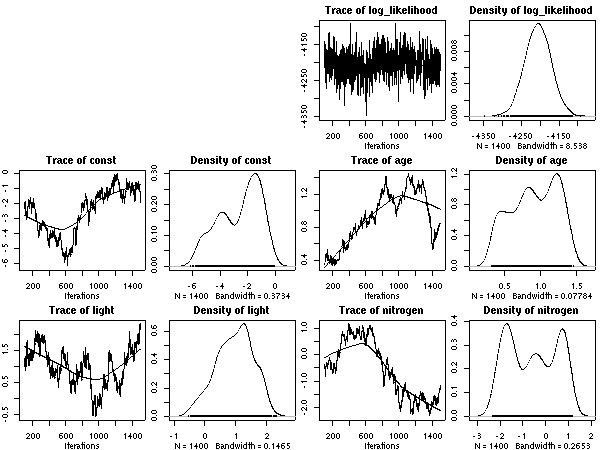
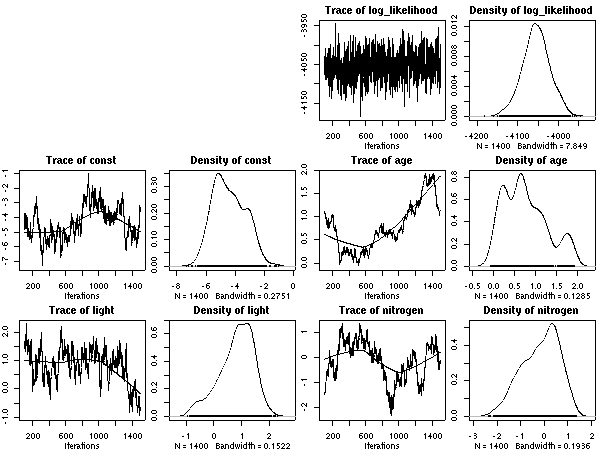
scale = 20
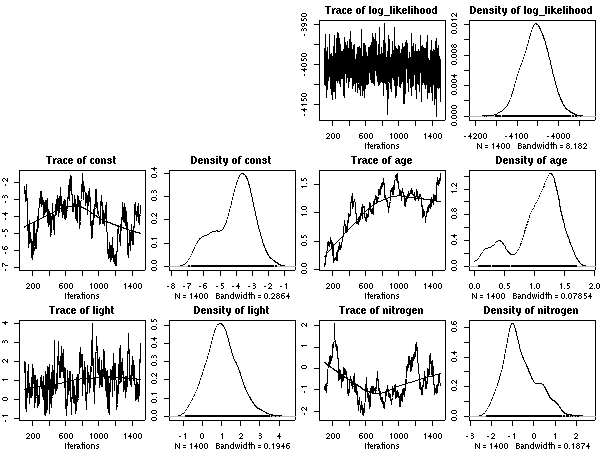
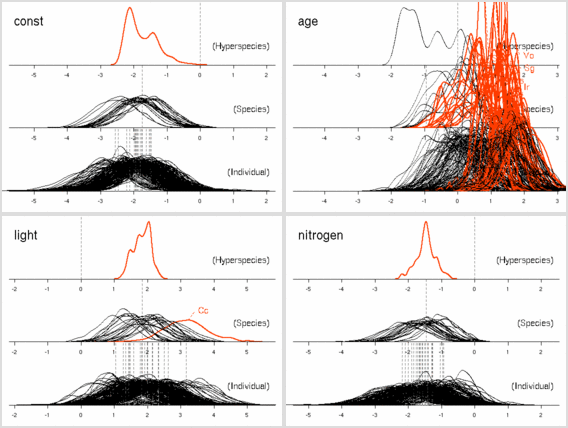
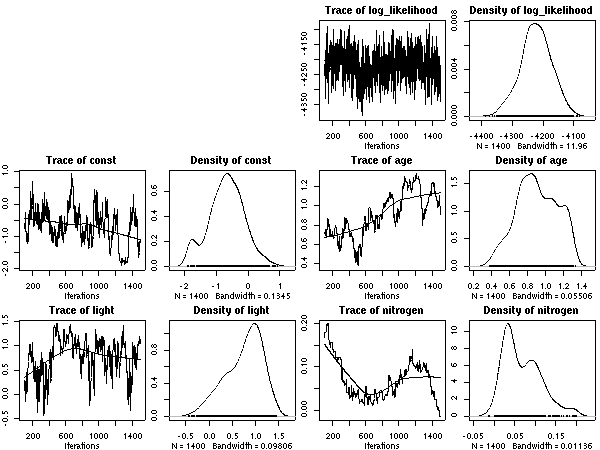
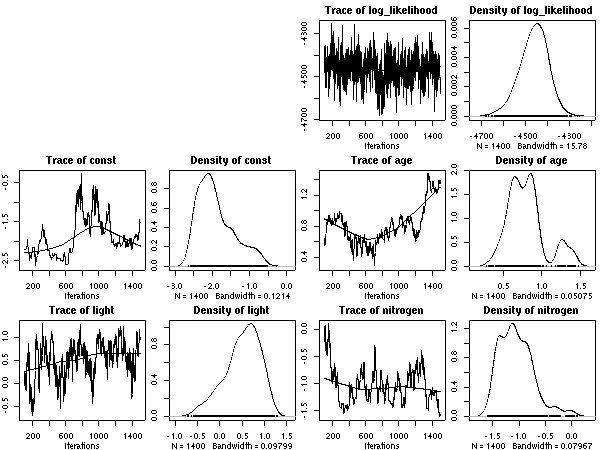
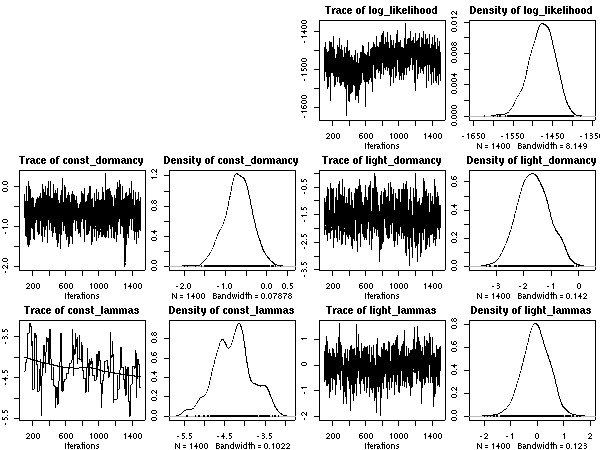
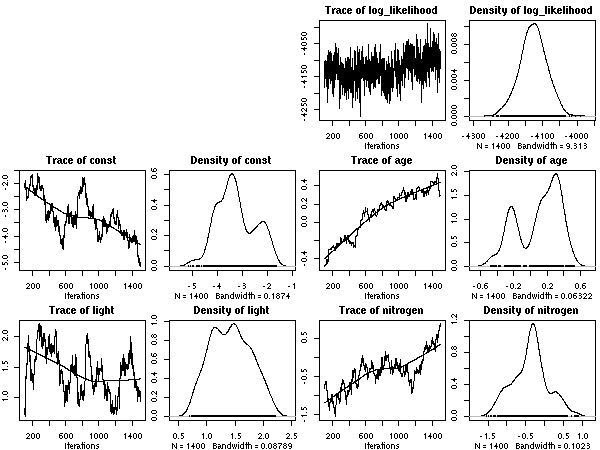
とした計算結果ひととーりでた．
これは 50 MCMC step とばしのサンプリング．
あまりかわりばえしないけれど，
ここに記録しておく．
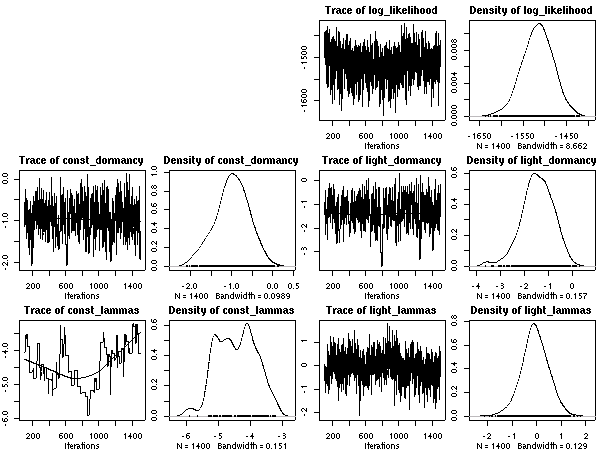
PriorGaussian
としてきたのを
PriorGaussianRandom
(超パラメーター数 1, 平均ゼロ)
と改名し，
こいつを Perl の @ISA
継承させて
PriorGaussianMixed
(超パラメーター数 2, 平均は HyperpriorGaussian
に生成させる)
とする，
で OK だろう．
1600 研究室着．
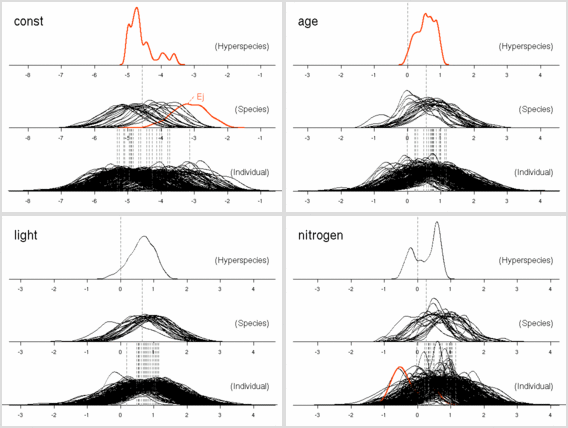
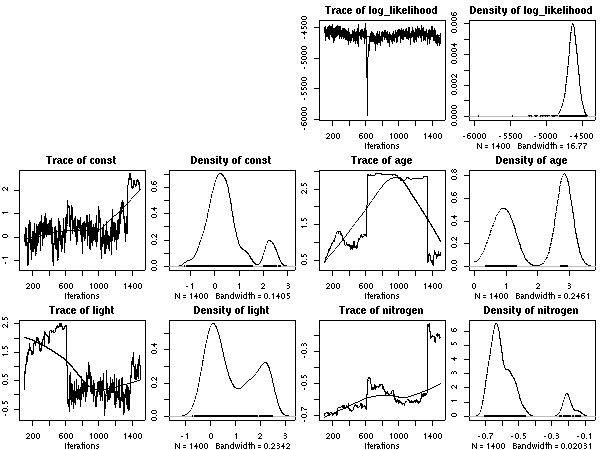
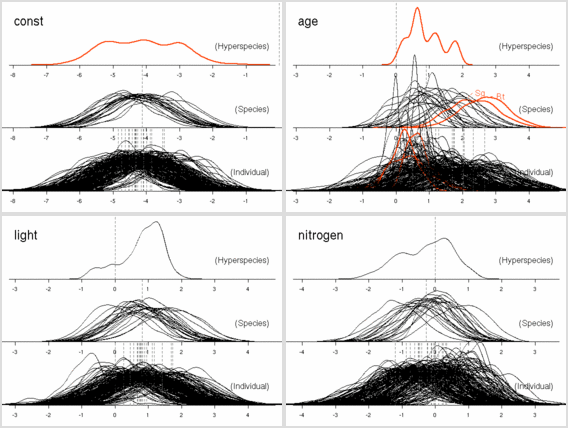
scale = 20
の 100 MCMC step とばし計算の結果でている．
まあ，
この方式の計算だとどうなるかは，
かなりの確信をもって予測できるようにはなった．
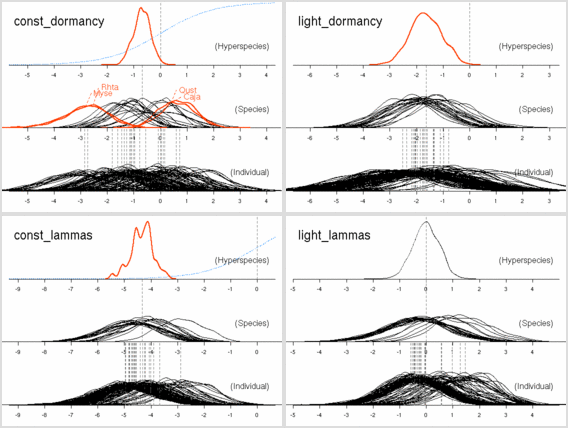
PriorGaussianRandom:
正規分布の事前分布，
平均はゼロに固定
(超パラメーター数 1)
PriorGaussianMixed:
PriorGaussianRandom
を継承，
ただし可変平均
(超パラメーター数 2)
PriorGaussianMixed
とし，
それ以外は
PriorGaussianRandom
とする．
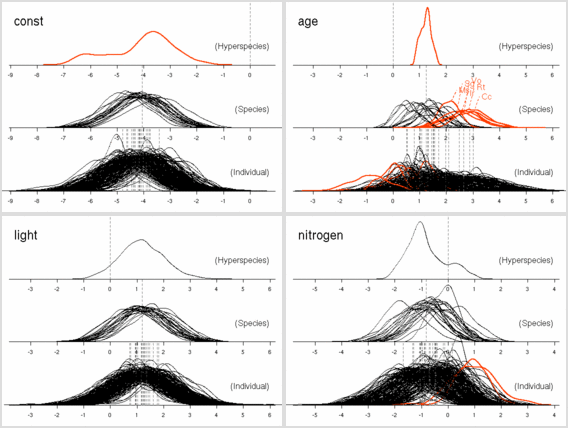
PriorGaussianMixed
を導入することで MCMC 計算の
「さらさら度」
がよくなった．
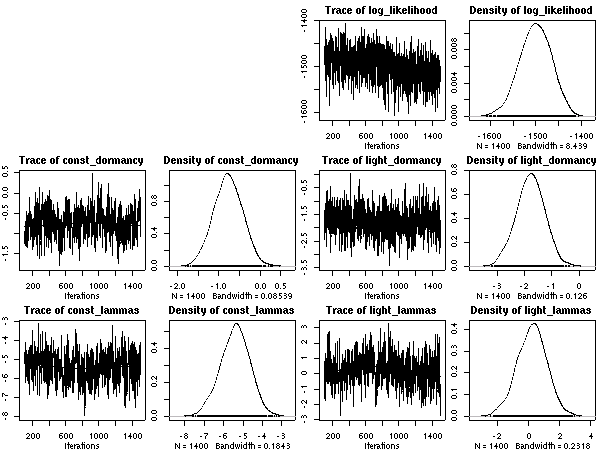
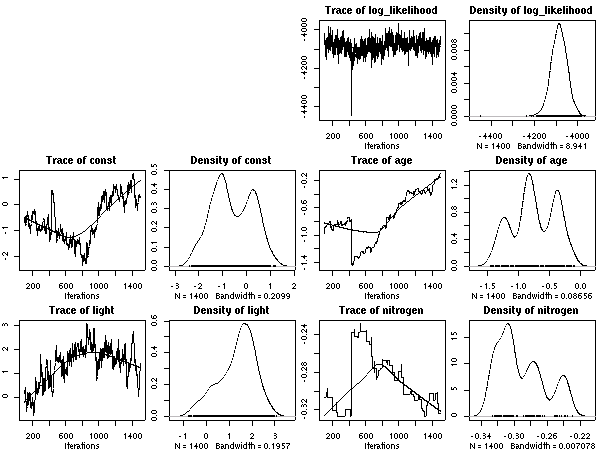
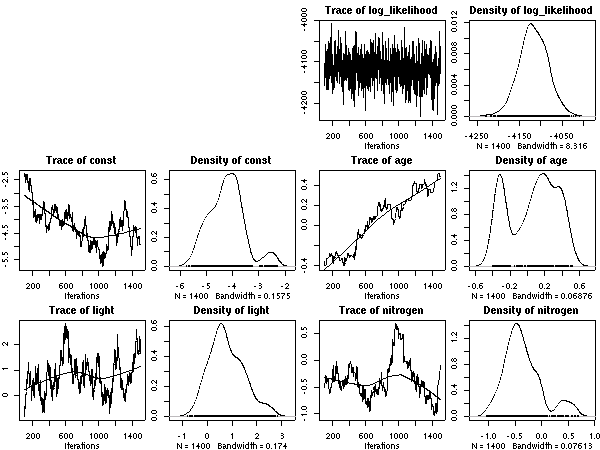
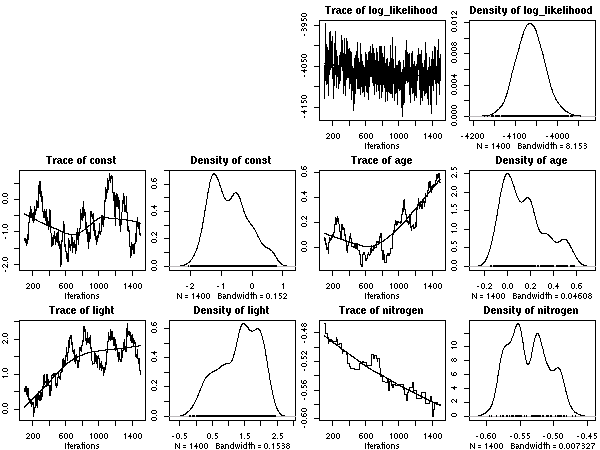
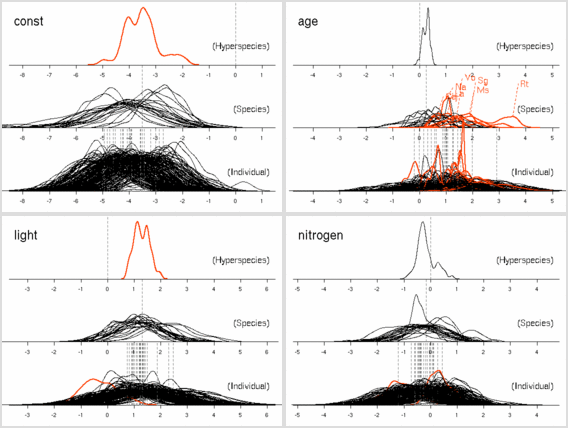
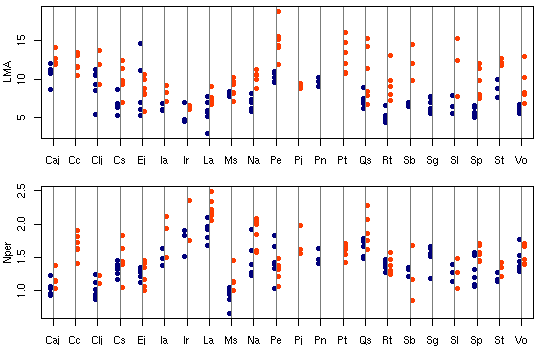
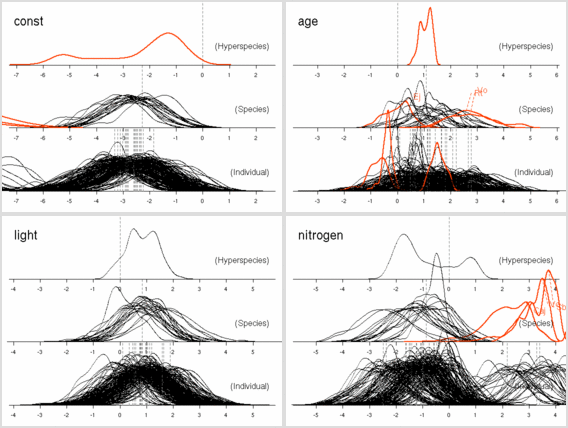
後記: ここは記述がまちがっていて (さいわいにも計算プログラム内ではまちがっていなかったんだけど)， Narea = Nmass * LMA が正しい． つまり， Narea なる量は LMA とほぼ同じ， ということ．LMA は葉重量窒素量にくらべて明るさとの交絡がキツいので， 「葉面積」モデルのほうの nitrogen は図示してるがごとくに， わけのわからぬものになりがちなのである．
scale = 10，
シュート伸長の休眠・二度伸びは昨日のものを使った
(こっちは 10 とばしで十分なのに)．
min(log(runif(1000000, 0, 1)))
とすると -14 ぐらいの値になる
(極値分布ですね)．
この程度のはずなんだが
……
HyperpriorGamma
に生成させる分散逆数は
……
かけることの exp(平均ゼロの正規乱数)
とでもするか．
これでも対称サンプラーだ．
1 + (1 + 明るさ) × 葉齢 + 窒素
となってるんだけど，
これを
1 + 葉齢 + 明るさ + 窒素
としてみたらどうなるかな?
ということで
50 MCMC step とばしにて計算を命じる．
林冠三次元構造を推定する MCMC 計算法
○久保拓弥 (北大・地球環境)・小林剛 (香川大・農)・加藤京子 (JST/CREST)
森林の林冠部における光強度の空間分布の実測値を用いて葉群配置を推定する新しい方法を提案する．植物群落 (林冠) の生産力を推定するためには，三次元空間上に分布しているそれぞれの葉群における受光量が必要である．しかし，林冠内すべての葉での受光量の直接測定は不可能である．これに対して，林冠を三次元格子で区分けし，各格子点における光量子密度の瞬時値は比較的測定しやすい．この観測による「三次元光分布データ」があれば，門司・佐伯モデルの考えかたを応用して葉群の分布と各葉群における光強度の推定が原理的には可能である．ところが，観測された三次元光分布を (おおよそ) 「再現」する葉群の配置は無数に存在し，光分布を再現可能な葉群配置ごとにデータへの「あてはまりの良さ」が異なる．これは「もっともらしい」葉群配置たちが Gibbs 分布に従うためである．そこで Markov Chain Monte Carlo (MCMC) 計算によって葉群配置の「サンプリング」によって対象林冠を「再構成」する方法を開発し，その妥当性を検証した．
林冠構造の推定に用いた三次元光分布データは北大雨龍研究林 (母子里) 内の 17 年生ダケカンバ林 (樹高 7-9m)で 2002 年 8 月に得られた．フォトダイオード (浜松ホトニクス) を 0.3m 間隔に配置したアレイを作成し (農環研・西村誠一博士による)，これを 3m×6m 方形区内で水平方向に移動させ，各格子点における光量子密度を測定した。さらに測定高度を 0.6m 間隔で変化させ，三次元光分布を得た．リター量から見積もった葉の密度なども参考にしつつ，光分布のデータから MCMC 計算によって林冠葉群配置を推定し，さらにこれを用いて林冠光合成生産量を算出した．
