ぎょーむ日誌 2006-01-(11-20)
2006 年 01 月 11 日 (水)
-
0800 起床.
ねむい.
朝飯.
コーヒー.
0900 自宅発.
晴.
0915 研究室着.
伊庭さんから MCMC 計算についていろいろとご指摘いただく.
ありがたいことです.
-
0920 研究室発.
0925 正門横の学術会館着.
センター試験の監督調教会.
入試課がまぬけなミスして会場移動などなど.
いつものごとき内容
……
しかし今回は悪夢のごときリスニングテストとやらが追加されたので,
説明がやや長い.
私は姑息にも第二日目 (日曜日) の監督を志願したので,
これにはわずらわされなくてもすみそうだけど.
アタマの中はいつしか MCMC 計算の改善方法の思考に占められてゆく.
1100 ごろ終了.
-
今回のセンター試験受験者数は 55 万人ぐらい
(前年に比べて 3% 減だそーで).
北大での受験者数は 5500 人ぐらい.
全受験者の 1% が北大にくるわけだ.
道内の受験者数は約 2 万人とのこと.
監督おしつけられるほうとしては,
どんどん受験者数がへってほしい.
-
昨晩から
(牛原さんには内緒でこっそりと)
計算させていた 100 MCMC step とばしの計算結果
……
あまりかわらんな.
それはそれでいいことなんだろうけど.
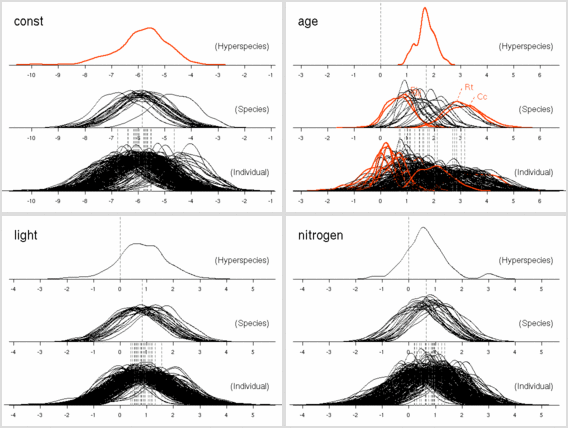
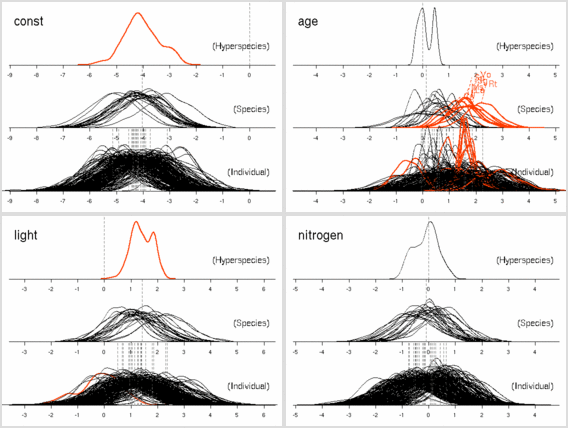
葉面積あたり窒素量モデル (LMA にちかい量)
葉重量あたり窒素量モデル
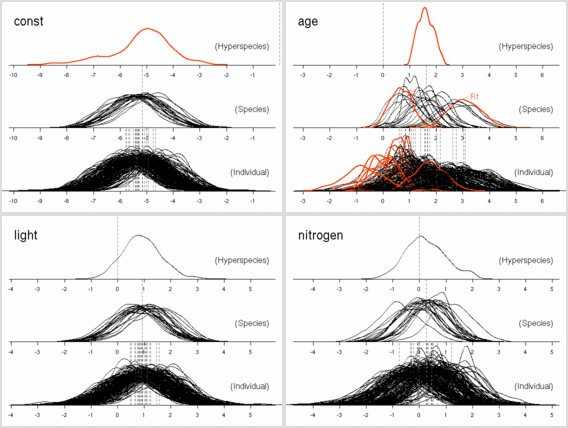
-
昼飯.
-
さて,
「センター試験監督ばいと」の説明会場で考えていた改造を適用してみる.
Hyperspecies の層において,
パラメーターの事前分布の平均と分散の超パラメーターを与える,
ってのがいま使っている方法.
これでも上のごとく推定はできるんだけど,
不必要にややこしいモデルを適用しているような気がする.
-
そこで,
hyperspecies の層においてだけ
無情報事前分布を導入し,
超パラメーターぬきで事後分布を生成させる,
という方式を試してみる.
Hyperspecies の下の species - tree においては,
これまでと同じく random effects 的な Gaussian prior,
つまり平均ゼロで分散逆数が超パラメーターで定義される
ガンマ分布に従う事前分布を使う
(でないと,
系全体の振動が大きくなりすぎる).
-
コードの改造は簡単にできた.
PriorGaussianNonInformative
なるクラスを定義し,
こいつに
HyperparameterNonChange
なるニセの hyperparameter を持たせる,
と.
-
「さっさと計算おわらせなさいよ」
と圧力をかけてくる計算発注者の牛原さんに隠れてこっそり試験運転開始.
ふーむ,
興味ぶかい挙動を
……
-
ひとやすみしてお茶部屋雑談.
ちかごろは Nature 掲載のグラフ (カラー)
なんかもゑくせる生成の原図から描き直されたみたいなのが
目につくようになっている.
私のごときゑくせる嫌いだけでなく,
ゑくせる依存症なヒトたちの中にもゑくせる図はカッコ悪い,
という意見は少なくない.
このように評判が悪いにもかかわらず,
ゑくせる図はなぜ使われるのか.
「見てくれがださい」と指摘されるとムキになって過剰対応する
Microsoft はなぜこれを放置するのか.
-
諸賢からいろいろな説明あったわけだが
……
亀山さん提唱の
「ゑくせる脳」仮説には関心 (かつ寒心) させられた.
その観察によると,
(特にお役所方面などで)
「数量をグラフ表示したときに,
ゑくせる図なら『なんとなくわかった』気分になれるけれど,
(同じ内容であっても)
それ以外のソフトウェアで作られた図を見せられても
まったく読みかたがわからない」
つまり「グラフによる数量把握」という脳機能がゑくせる図という形式に最適化
(しかも極度に最適化)
されてしまった「ゑくせる脳」もったヒトたちが増えつつあるので,
Microsoft もグラフまわりをうかつには改変できない,
というものである.
これがホントだとすると,
世の中,
いったいどうなってしまうんだろうね
……
-
かくれ計算のかくれ試行錯誤つづく.
-
夜になって生態学会さーばーのぞいてみる.
本日は新潟大会の要旨しめきりなんだけど,
まあ,
ぜんぜんこんでないので安心して放置.
-
しかしここ A 棟 8F では要旨書きをきっかけに
人生にナヤんでしまうヒトたちがうろうろしていて,
お茶部屋に拘束されてしまう.
なんだかよくわからないけど要旨かいてしまって,
やっぱり自分でもよくわからないから見てくれとか,
データに傾向がでているはずなのでこう書いたというので
データ見せてもらっても単なるノイズにしか見えなかったり,
などなど
……
-
よーやく釈放されて
2410 研究室発.
2425 帰宅.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0820):
米麦 0.5 合.
タマネギ・ニンジン・セロリ・ブナシメジ・タチのシチュー.
- 昼 (1310):
研究室お茶部屋.
米麦 0.5 合.
タマネギ・ニンジン・セロリ・ブナシメジ・タチのシチュー.
- 晩 (2450):
米麦 0.7 合.
ネギ卵炒飯.
海藻スープ.
2006 年 01 月 12 日 (木)
-
0700 起床.
朝飯.
コーヒー.
洗濯.
-
昨日からつづけている隠れ計算
(hyperspecies の層において事前分布を無情報化する),
ひと区切りついたのでここに記録しておく.
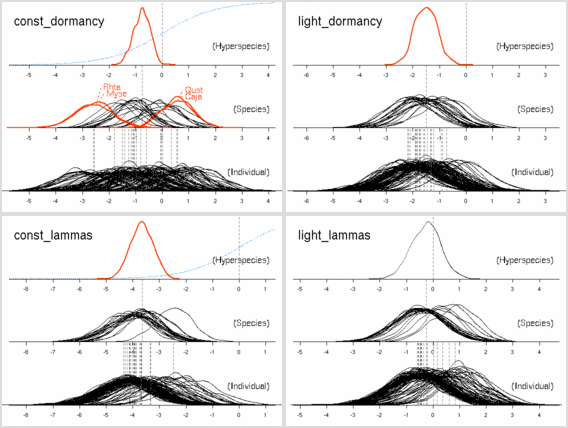
まずはシュート伸長の休眠・二度伸びの確率モデル.
10 MCMC step とばし.
これは (データが単純なので)
どういうふうに計算してもあまり変わらない.
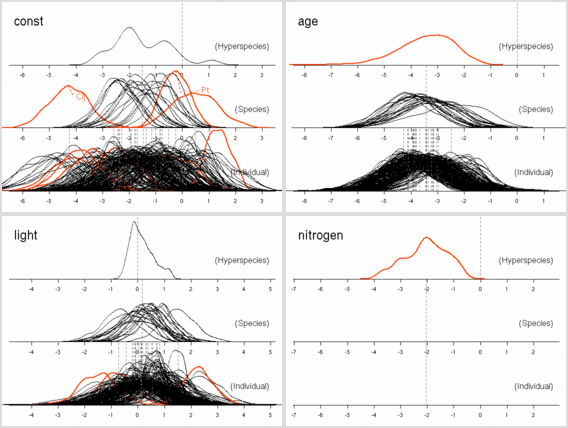
シュート伸長の休眠・二度伸び
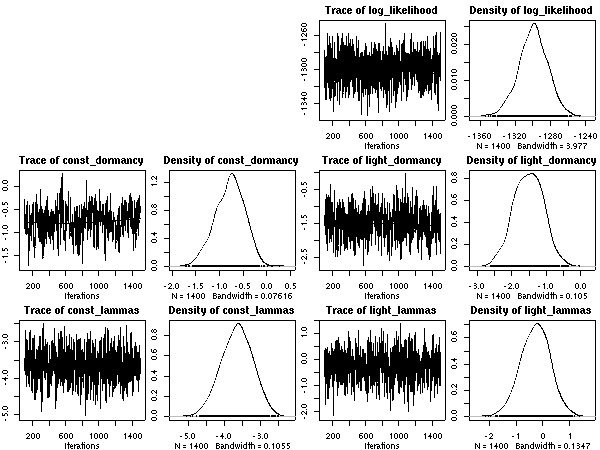
-
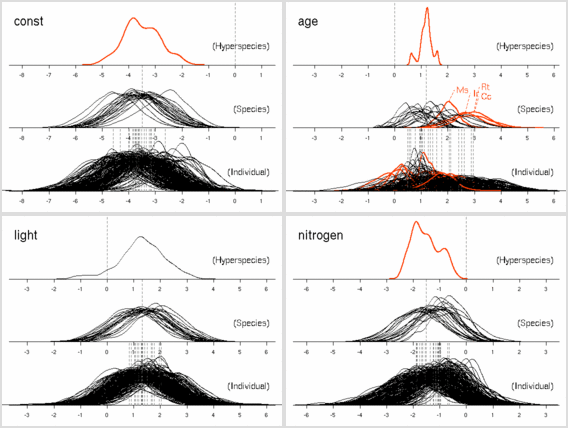
つぎに葉っぱ死亡確率のモデル.
50 MCMC step とばし.
これにはふたつあって,
まずは
1 + 葉齢 + 明るさ + 窒素
つまり「明るさが葉っぱ死期を早める (あるいは遅くする)」
モデルから.
シュート伸長の休眠・二度伸び

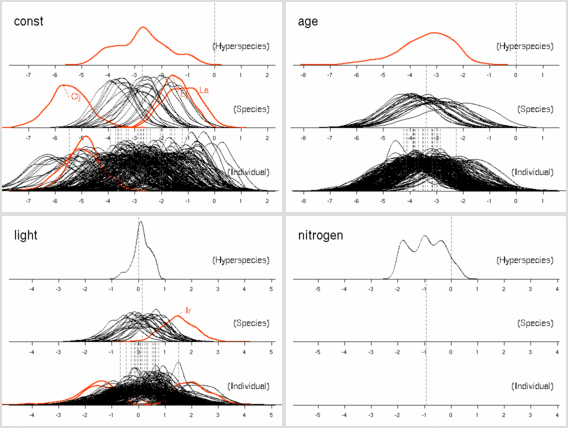
葉面積あたり窒素量モデル (これはかなり LMA に近い量)
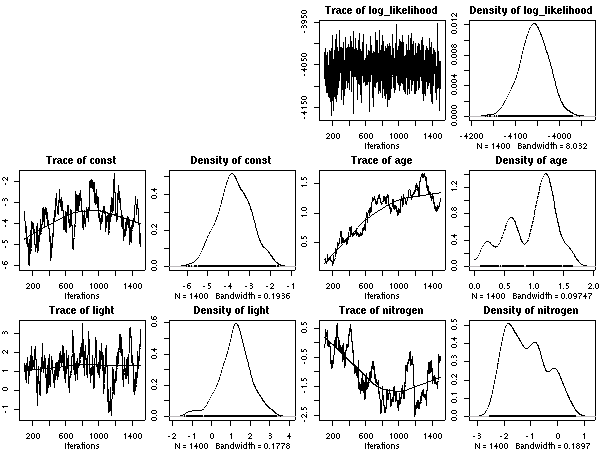
葉重量あたり窒素量モデル
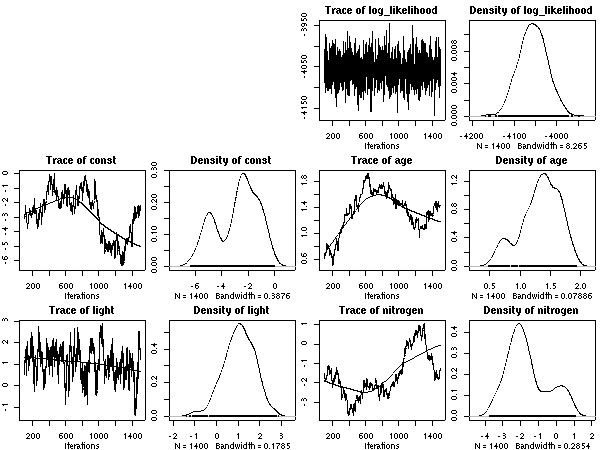
-
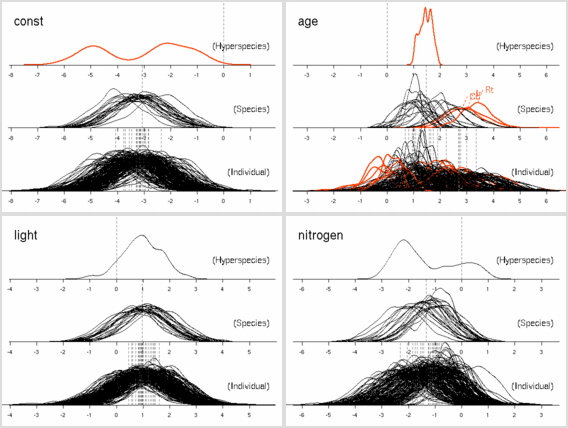
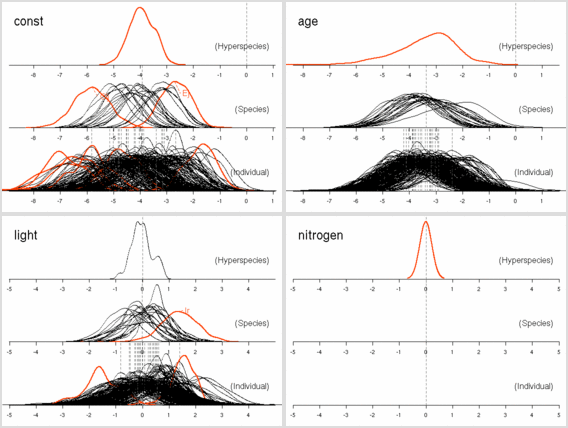
つぎは
1 + (1 + 明るさ) × 葉齢 + 窒素
つまり「明るさが葉っぱ『老化』を加速する (あるいは減速する)」
モデル.
葉面積あたり窒素量モデル (これはかなり LMA に近い量)
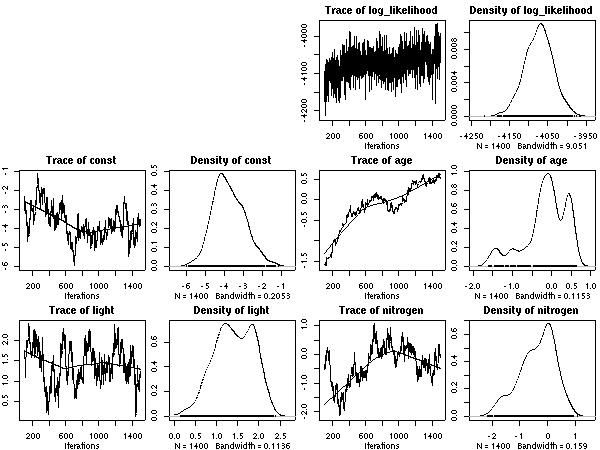
葉重量あたり窒素量モデル
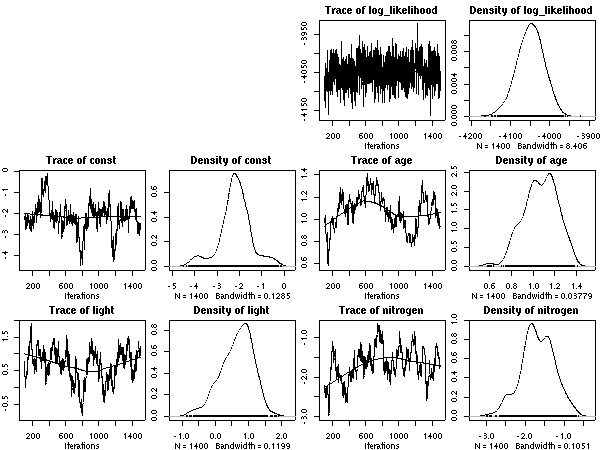
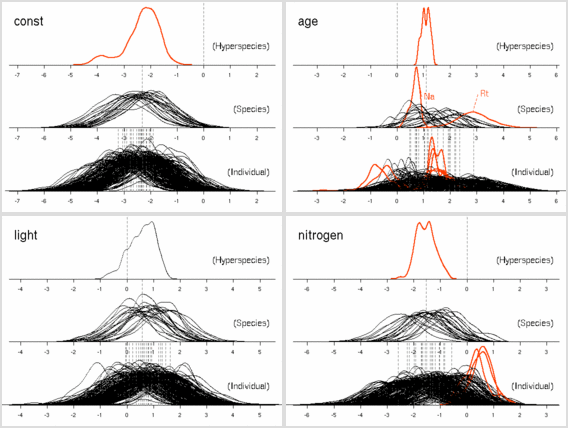
-
現時点でだいたいわかってきたことは
……
-
葉っぱの一年間の死亡確率は定数ではなく,
葉齢に依存して上昇する.
樹種によってはこの値が極端に高いものがあり,
これは明るさなど他の要因とはあまり関係なく,
短期間のうちに葉っぱを脱落させる樹種である.
-
明るい場所では (だいたいにおいて)
葉っぱの「老化」
(ここでは葉っぱの死亡確率が高くなること)
の開始が早いもしくは老化が加速している
(葉齢にともなく死亡確率の上昇が大きくなる).
しかしながら,
そうでない樹種もいるので,
明るさ依存性のばらつきは大きい.
後述する窒素との交絡もある.
-
重量あたり窒素量は
(おそらくノイズが多いため)
影響がよくわからない,
あるいはモデルによっては葉っぱの老化開始を遅くしている.
しかしながら,
モデルによってはばらつきが大きい.
その原因はふたつ考えられる.
ひとつは樹種によっては窒素が老化時期を早めている
可能性があるため.
もうひとつは,
樹種によっては「明るいと窒素が多い」
という交絡があり,
「明るさ」を窒素量で代用できる場合があるため
(パラメーターの遷移をみていると,
明るさと窒素の変動には負の相関がある).
-
面積あたりの窒素量
(これはほとんど LMA に近い)
の影響もよくわからない,
あるいはモデルによっては葉っぱの老化開始を遅くしている.
まあ,
これぐらいはこれまでの計算結果から言っていい範囲だと思う.
-
「樹種差」なるものを random effects とする
今回の新しい試みの利害得失はどんなものかしらん.
この屋久島データみたいに,
多樹種 (22 樹種) で樹種ごとの標本数が少ない
(各樹種最大 12 標本しかない)
という状況ではこれしかパラメーター推定の方法はなさそうだ
(このあたりもうちょいよく考えてみたい).
しかしながら同時に,
「樹種差」なるものの変化があまり「連続的」ではない場合,
hyperspecies の層において事後分布は「多峰的」になってしまう.
-
そしてこのように単純にベイズモデル化したところで,
交絡 (confounding) の問題が自動的に解決するわけではない.
パラメーターの遷移をみることで,
「あ,
交絡してやがるな」
というのがわかりやすくはなったけれど.
-
ところで書き忘れていたんだけど
……
いつも割り算値をイヤがっているぎょーむ日誌で割り算値記述がまちがっていた
(訂正の文を二日前に追加しといたんだけど).
ここでいう「面積あたり窒素量」なる数量は,
重量あたり窒素量 (これは測定機械が吐きだす割り算値)
×
LMA (これは人間が計算した割り算値)
で計算している.
計算プログラムの中ではそうなっていたんだけど,
ここに書いたときには LMA でわることにされていた.
嗚呼.
-
1030 自宅発.
雪.
1045 研究室着.
-
ここまでの計算結果,
いろいろと検討してみる
……
計算改善アイデアもつきてきた.
まあ,
こんなところなのかな.
-
ふと,
species の層において分散逆数は種間で共有するけれど
平均は樹種ごとに異なるガウシアンな事前分布としてみたら
……
とゆー夢想にとりつかれてしまったんだけど,
これ以上滞納してたら計算発注者に見つかって怒られそうなんで,
ここまでの結果から
寿命分布など計算するプログラム作りフェイズに移行していく.
-
そういや,
来週の東京出張の準備はまだ何もしてないや.
そのあとの M1 授業の準備も.
気が重い.
-
A 棟 7F の愛煙家某先生からのメイル.
喫煙は、平均寿命を縮める。よって、他の死因の発生確率が下がる。例えば、喫
煙者は、交通事故による死亡率は非喫煙者より低くなる。よって、喫煙は交通事
故による死亡率を下げる(良い)効果がある。なお、「交通事故」の部分は、他の
事故名や喫煙とは無関係の病名に変えても良い。
んー。そうだったのか。
私の返信.
喫煙者は注意深くて,非喫煙者より交通事故にあう確率が低い,と仮定してみ
ましょう.この場合,交通事故にあう確率が低くなることで,そのぶん喫煙に
よって死ぬ確率が高くなってしまいます.おそろしいことです.
喫煙者は喫煙による死亡確率を下げるために,より不注意になって頻繁に交通
事故を起こして交通事故で死ぬ確率を高めるべきです.
-
昼飯調達のため北大生協へ.
吹雪.
研究室にもどって昼飯.
時刻はすでに 1500.
-
(膨大な量になる)
推定結果と観測データを対応づけるいろいろな
R
プログラミング.
-
1930 ごろひととーりできた
……
が,
これがじつにじつに驚くべきものばかり.
階層ベイズモデルだのマルチレイヤーモデルだのの理解がまだまだだ,
というのがわかった.
うん.
計算あれこれ全部やりなおしだな.
-
とりあえずモデルは
1 + (1 + 明るさ) × 葉齢 + 窒素
で計算してみる.
-
パラメーター推定の結果との食い違いが一番いちじるいしいのはココだ
……
個々の個体ごとに特定されるパラメーターから計算した
平均葉寿命と重量あたり窒素量の関係はかくのごとし.
あたかも窒素が多いと短命であるかのように見える.
あとで説明するように,
これは「明るさ」との交絡なのである
(明るいところ: ○).
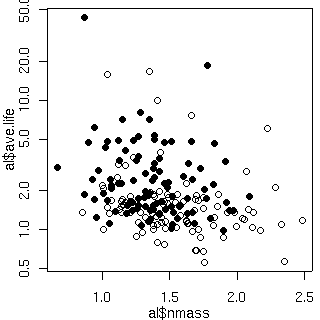
[推定平均葉寿命 vs 窒素量]
推定平均葉寿命の単位は年.
葉っぱ内の窒素量の単位は重量パーセント.
あとで説明するように,
いくつかの個体では「齢」依存性パラメーターが負になっているので,
ここではそれをゼロとおいて計算している.
-
Hyperspecies と species の層においては
nitrogen のパラメーター推定値は
ほとんどマイナスの値になるのにもかかわらず,
なぜ上のように見える図ができてしまうのだろうか?
じつは樹木個体のパラメーターにおいて「調節」がなされていた.
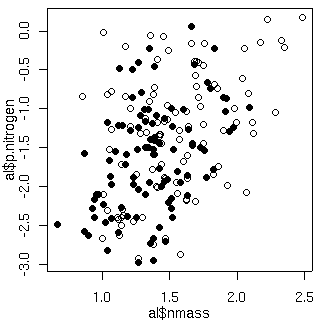
[窒素パラメーター vs 窒素量]
縦軸がパラメーター事後分布の平均値.
窒素量が少ないほど値が低い (長命化)
と推定されている.
こういう個体の窒素量に引きずられた推定結果が妥当なのかどうかは,
あとで検討してみる.
-
こういう関係があると,
当然ながら線形予測子の部品としては
「窒素」コンポーネントは
下の図のごとく「ノイズ」に近い
……
つまりこのベイズ推定で
「モデル選択」ができていれば削除されるような要因なのである.
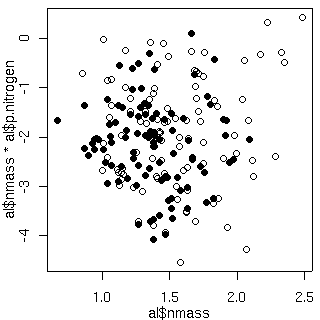
[のいず]
縦軸は個体ごとの窒素パラメーターとその個体の窒素量の積.
この図は何を表しているかというと,
窒素量の大小は葉っぱ死亡確率に何の影響もおよぼさない,
ということ.
-
じゃあ,
何で nmass とやらの大きいところで早死にしているかといえば,
明るい場所だから,
ということになる.
-
つまりまとめると,
-
全個体の窒素量 (nmass) の勾配は
死亡確率の大小と対応しない
(上の「のいず」図)
-
明るい場所では葉っぱは早死にする
-
葉内の窒素が極端に多い (2% より大きい) 場合,
それは明るい場所に限定される
-
窒素が極端に多い場合に早死にしている理由は
「明るいから」とするほうが妥当である
ということ.
-
いやー,
いろいろと検討すべきことがあるな
……
-
まずは窒素まわりで残された問題からいこうか.
ここで問題なのは,
hyperspecies - species - tree の層において,
hyperspecies - species までならば明らかに
「窒素が多ければ死亡確率は低下」に見えた現象が,
個体内での補正 (上の図) とでも言うべきパラメーター推定によって,
「窒素と死亡確率は無関係」
となったことだ.
-
これは (このモデルのもとでは)
窒素はほとんど死亡確率を説明できない,
という結果を階層間のややこしい調節で実現してしまったんだろうな.
すると
なぜ hyperspecies - species ではマイナスになったのだろうか?
ゼロを中心にして反転した結果でもさしつかえないように思える.
これは「明るさ」との交絡のせいではないかな.
つまり,
窒素のほとんどの値域では相関ナシでもよいけれど,
右端の窒素が極端に多いところでは高い値であってほしい,
と.
-
実際のところ
(上の比較では使っていないほうのモデルである)
1 + 葉齢 + 明るさ + 窒素
モデルのほうではしょっちゅう
「ゼロを中心にした反転」が発生していたわけで.
-
このあたりすっきり解決するためには,
モデル選択が必要かな.
べいぢあん世界でのモデル選択となると,
またいろいろと勉強してプログラムをかなり改造せんといかんような気もする
……
これの検討はいったんおく.
-
他にもいろいろと問題ある.
たとえば齢依存性だ.
これは自由に選ばせたらダメだね.
「全体的にはプラス」であっても個体の中には
マイナスの値をとるやつがでるからだ.
「生き残るほど死亡確率が下る」
というすっとぼけた個体がいたっていいぢゃん,
と気楽にかまえていたんだが
……
というのも x 才までに死ぬ確率は単調に増大していくだろう,
などと思いこんでいたわけなんだけど,
実際はそうではなかった.
ある齢から確率 1 で生きのびるやつもでてきた.
いやはや.
-
解決策としては事前分布を変えるしかない.
葉齢にまつわりつくパラメーターは常に非負の値をとる事前分布を使う,
と.
-
モデル選択はあとまわしにして,
とりあえずこのへんからとりくんでみるか.
あるいは事前分布を変えるのではなく,
ガウシアン事前分布から生成されたパラメーター
p
を exp(p)
として使う,
とか?
-
ものの試しとて葉齢まわりに
exp()
かませる試運転
……
ふーむ,
まあしばらく放置.
-
次に個体ごとに窒素パラメーターとかを自由に選ばせてよいのか,
という問題だよな.
面倒なことはやめてモデル選択でケリをつけるのか.
それとも,
モデリングでもう少し工夫すべきなのか.
-
時刻はすでに 2210.
晩飯でも調達するか.
年末に 北 11 西 4 に新しくできた Sunkus までふらふらと.
研究室にもどって晩飯.
-
応急処置的な対策として,
窒素量を全部種内平均値に置き換える,
という方法を採用することに.
というのもここで興味あるのは種内差ではなく,
窒素量の種間差が葉っぱ生き死ににどう関与するか,
を明らかにすることだから,
というような理由になるか.
Hyperspecies - species - tree の各層に
Replace_nitrogenSPC()
なるメソッドを追加してみる.
-
そういや甲山さんが「(窒素量の)
種内差と種間差は意味が違う」
と言ってたのはこういう意味だったのかなあ.
-
試行錯誤で関数型など変えつつ試験運転つづく.
上で
ここで問題なのは,
hyperspecies - species - tree の層において,
hyperspecies - species までならば明らかに
「窒素が多ければ死亡確率は低下」に見えた現象が,
個体内での補正 (上の図) とでも言うべきパラメーター推定によって,
「窒素と死亡確率は無関係」
となったことだ.
とか書いてるけど,
じつは
-
種間では「窒素多いと長命化」
-
種内では「窒素多いと短命化に見える」
(実際には「明るさ」との交絡)
となってるような結果が得られつつあるような気がする.
-
真夜中すぎ,
10 MCMC step とばしの粗い計算結果
(まだ収束も十分ではない)
が得られた.
あとで自分で見てわからなくなるので補足しておくと,
-
線形部品の
age と light
は exp()
内の量である
-
nitrogen
は hyperspecies の層だけにパラメーターがある
で,
パラメーターの事後分布だけみると,
たしかに窒素量が (初期) 死亡確率を引き下げてる,
ってのがはっきりしてるみたいなんだけど
……
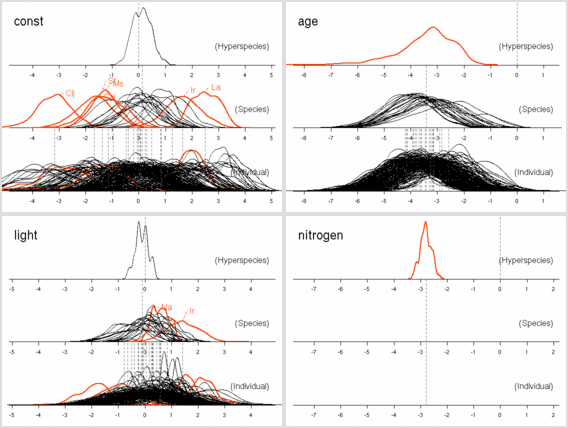
-
しかしながら,
全個体に関して葉の平均寿命を計算して,
その樹種ごとの平均窒素量とやらと比較しても
いまいち明確ではない.
ふーむ?
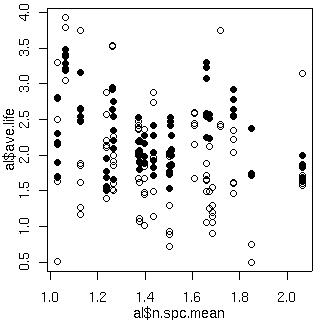
[推定平均寿命 vs 窒素]
窒素はほとんど無関係,
に見えるが
……
横軸の重量あたり窒素量の種内平均値は平均寿命を伸ばすはず,
なんだけど?
まあ,
窒素は葉齢の効果にかかる項ではないんで,
単に
「死亡確率が高くなる時期は遅くなる」
(その後の死亡確率上昇は高い)
ということなのかもしれないけれど.
-
なんかまた交絡してるのか.
あるいは死亡確率の関数型の問題か?
よくわからぬまま撤退.
50 MCMC step とばしの計算を命じておく.
2550 研究室発.
2605 帰宅.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0830):
食パン.
- 昼 (1500):
研究室お茶部屋.
北大生協サンドイッチ.
- 晩 (2230):
Sunkus サラダ巻.
295 円.
2006 年 01 月 13 日 (金)
-
0900 起床.
朝飯.
コーヒー.
1045 自宅発.
晴.
1100 研究室着.
-
昨晩かなり方針転換した屋久島葉っぱ寿命計算,
50 MCMC step とばしの結果が出た.
重量窒素量モデルだと収束はそこそこか.
ど忘れしそうなんで
(作図プログラムをさっさと改めるべきだな),
また書いておくと
……
-
線形部品の
age と light
は exp()
内の量である
-
nitrogen
は hyperspecies の層だけにパラメーターがある
葉重量あたり窒素量モデル
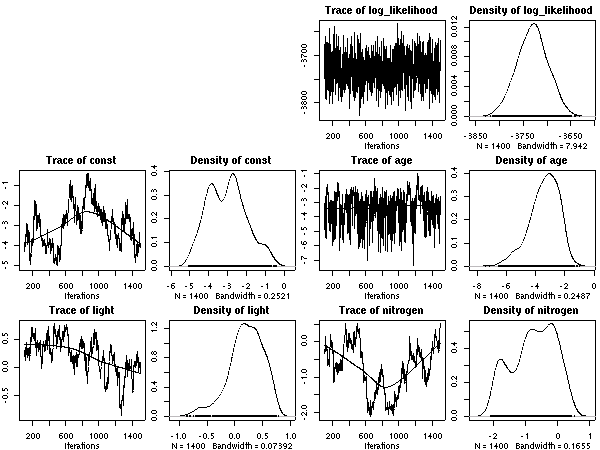
-
これの (推定) 平均葉寿命 vs (種内平均) 窒素量はこうなる.
Hyperspecies におけるパラメーター事後分布のとーり,
この窒素量は寿命とはあまり関係ない.
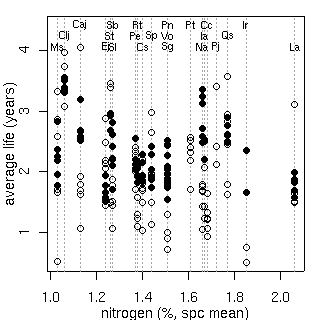
[平均寿命と葉内窒素量]
樹木個体ごとに計算して推定平均葉寿命の単位は年.
葉っぱ内の窒素量
(種内平均値)
の単位は重量パーセント.
○が明るい場所.
全般に明るい場所のほうが寿命短い.
しかし個体ごとにみていくと,
必ずしもそうはなっていない場合もある.
後記:
ここで図示してたのは平均葉寿命 (死亡時葉齢の平均値ではなく)
平均葉齢だった
……
訂正版は 15 日に.
-
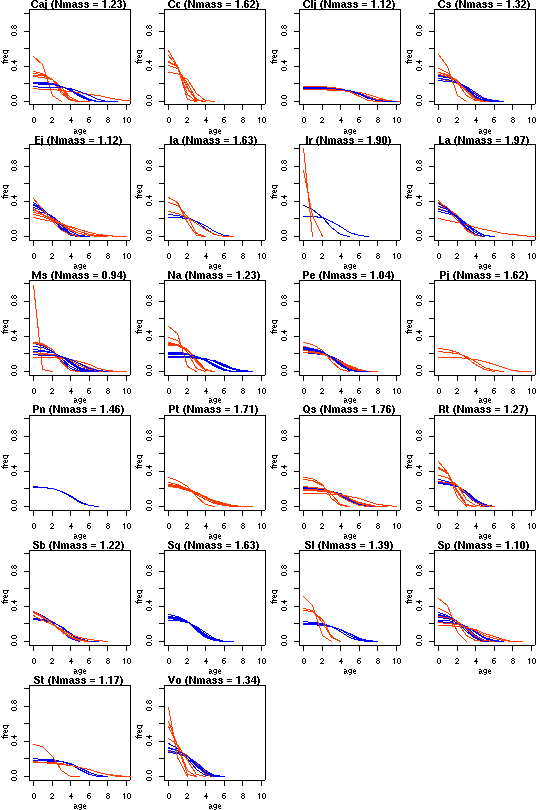
上の図のもとになるのは,
こういう樹木個体ごとの葉齢分布だ.
全 22 樹種 195 個体.
推定されたパラメーターから再構成されたもの.
個体差も入っている.
-
パラメーター推定がヘンになってないかどうかをチェックしておくか.
まず種内平均値とかいう窒素量は,
> (vn <- tapply(d0$Nper, d0$sp.ab, mean))
Caj Cc Clj Cs Ej Ia Ir La Ms
1.1274 1.6848 1.0637 1.3963 1.2388 1.6717 1.8478 2.0641 1.0313
Na Pe Pj Pn Pt Qs Rt Sb Sg
1.6605 1.3734 1.7203 1.5064 1.6077 1.7730 1.3779 1.2652 1.5140
Sl Sp St Vo
1.2686 1.4350 1.2639 1.5053
> sort(vn)
Ms Clj Caj Ej St Sb Sl Pe Rt
1.0313 1.0637 1.1274 1.2388 1.2639 1.2652 1.2686 1.3734 1.3779
Cs Sp Vo Pn Sg Pt Na Ia Cc
1.3963 1.4350 1.5053 1.5064 1.5140 1.6077 1.6605 1.6717 1.6848
Pj Qs Ir La
1.7203 1.7730 1.8478 2.0641
……
となっている.
まあ,
こんなふうに「平均値」とか計算してしまってよいのか,
というのはよく考えねばならんところだけど.
全体 (hyperspecies) では窒素の影響はゼロまわりにあるのに,
なにかみょーな傾向を作りだすとすれば,
それは定数項 (const)
で,
ということになる
(窒素に関しては species - tree のパラメーターがないので).
そこで,
const
の事後分布を樹種ごとに集計してみる.
> (vp <- tapply(al$p.const, al$spc, mean))
Caj Cc Clj Cs Ej Ia Ir La Ms Na Pe
-4.0325 -2.9567 -5.7822 -2.4042 -1.4108 -2.7917 -1.4450 -1.1217 -3.5808 -3.8033 -2.6600
Pj Pn Pt Qs Rt Sb Sg Sl Sp St Vo
-2.9200 -3.4333 -1.5117 -3.3558 -2.7925 -1.8383 -2.5200 -3.7600 -2.6958 -3.7750 -1.9750
> sort(vp)
Clj Caj Na St Sl Ms Pn Qs Cc Pj Rt
-5.7822 -4.0325 -3.8033 -3.7750 -3.7600 -3.5808 -3.4333 -3.3558 -2.9567 -2.9200 -2.7925
Ia Sp Pe Sg Cs Vo Sb Pt Ir Ej La
-2.7917 -2.6958 -2.6600 -2.5200 -2.4042 -1.9750 -1.8383 -1.5117 -1.4450 -1.4108 -1.1217
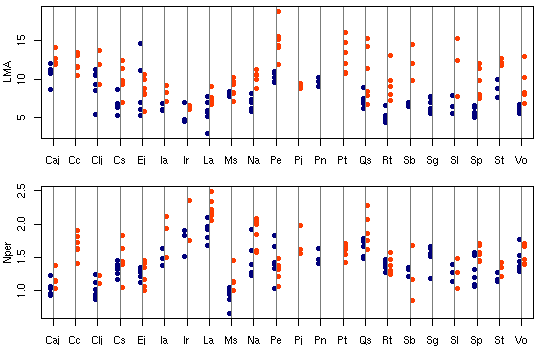
窒素 (vn)
と樹種ごと・個体ごとに決められるパラメーター
(vp)
のあいだにみょーな関係はなさそう.
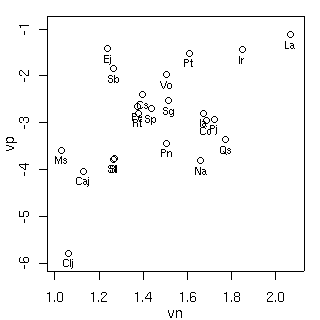
[vp vs vn]
図にしてみるとこうなる.
窒素が少ないところにサカキ (Clj),
多いところにバリバリノキ (La)
があるんでそちらに注意うばわれてしまうわけだが
……
const
において樹種差を random effects としてあつかっているので,
この程度では「傾向あり」とはならない.
-
そもそも,
この標本セットでは窒素量は樹種差とかあまりないんだよね.
ここから葉っぱの死亡確率を「説明」できる情報がひきだせるか,
ということだ.
もちろん「明るさ」との交絡は除外したうえで,
ということで.
-
「葉面積あたり窒素量」
(ということになっている量)
モデルのほうは 50 MCMC step の 1500 sample ではまだまだ収束してません,
というかんぢ.
個体ごとに平均寿命計算してみたけど,
すごくヘンだ.
明暗の効果が個体差でキャンセルされたり.
葉面積あたり窒素量モデル (LMA にちかい量)
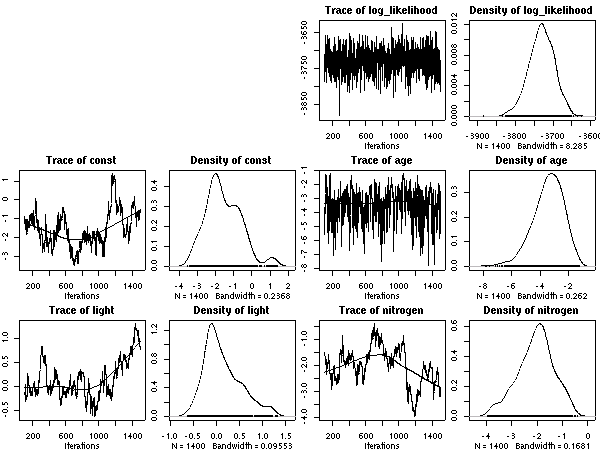
-
作図プログラムを改造したり,
データ整理・バックアップしてから,
検算もかねて今度は 100 MCMC step とばしで計算全部やりなおし.
明朝までには終了するだろう.
-
昼飯.
-
A802 のプリンター CANON LBP-2810 の印刷面黄色よごれ問題,
たぶんまた再生トナーカートリッジの不調だろうと交換してみたら,
なおった.
残量 10% 以上ある問題カートリッジは回収してもらうことに.
ついでに再生トナーカートリッジ屋に状況説明の手紙かく.
一本ぐらいおまけしてくれないものだろうか.
さらに,
LBP-2810 用の予備カートリッジは黄だけでなく黒・青も必要なので,
予算消化要請のきた東科研を充てる.
-
そういやアリのモデリングとか何もやってなかったな.
今年度は無理です.
-
屋久島まわりの作図プログラム点検・整備.
本日は,
もはや体力がつきてきた.
アタマの中もホワイトアウトぎみ
……
-
夕方,
キビしい計算発注者・牛原さんにモデル変更の説明と,
新しく得られた結果の説明をひととーり.
-
早々に撤退.
1835 研究室発.
1910 帰宅.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0920):
食パン.
- 昼 (1350):
研究室お茶部屋.
食パン.
タラすり身だんごカレー.
- 晩 (2030):
米麦 0.7 合.
タラすり身だんごカレー.
麻婆豆腐.
2006 年 01 月 14 日 (土)
-
0910 起床.
朝飯.
コーヒー.
怠業.
-
1235 自宅発北大構内走.
曇天.
1330 帰宅.
体重 73.2kg.
昼飯.
-
来週の東京出張の準備すらできてないのに,
3 月の東京出張の予定が確定する.
-
3/8 (水) ANA4726 千歳 (2055) → 羽田 (2225)
-
3/10 (金) ANA4715 羽田 (1040) → 千歳 (1210)
-
宿泊はまたしても
蒲田東口
-
1550 自宅発.
曇.
1605 研究室着.
-
計算発注者に結果ひきわたし後もつづく検算.
昨日命じておいた計算は終了してるわけだが
……
hyperspecies の層において窒素の影響は「長命化」.
しかし昨日のように推定平均寿命と比べてみると,
ほとんど影響なし.
原因を調べてみると,
定数項の species の層で「補正」していやがった.
-
窒素については,
「明るさ」との交絡をぬいてしまえば,
おそらくほとんど影響なし,
少なくともこの屋久島データでは何か傾向があるようには見えない.
しかしながら,
MCMC 計算でパラメーター推定させると,
なぜかしら hyperspecies の層においては「長命化」となることが多い.
「影響よくわからん」より頻繁である.
「短命化」はまったくないのに.
-
なんで線形予測子の構成要素間で「補正」というかつじつまあわせが
わざわざ出現するのか.
これをやると事前分布の尤度が低くなるんだけどなぁ.
そしてつじつまあわせをするにしても,
なぜ hyperspecies の層では「長命化」の方向にずれがちなのか.
なぞ.
-
よくわからんので次の検算.
$hyperspc->Set_unused_parameters(['nitrogen']);
を指定
(パラメーター値はゼロ,対数尤度もゼロに固定),
あとは同条件で計算してみよ
……
モデル選択的な設定,
と申しますか.
ふーむ,
やはり対数尤度はほとんど同じぐらい,
いや明らかにこちらのほうがマシそうだ.
葉内窒素量は葉っぱの死亡確率を説明するのに何の役にもたたんノイズなのか?
妥当な気がするンだけど.
-
1730-2000 お茶部屋にて塩寺さんのデータ解析こんさる.
またしても葉っぱ寿命問題.
牛原さんの屋久島葉っぱデータとの相違は,
-
熱帯山地林 (インドネシア),
暗いところ (林床?) の調査
-
木本・草本・シダなどなど (種数 110 弱)
-
葉っぱ追跡型データ (30ヶ月 ぶん),
葉っぱごとに出現とその消滅まで
(むろん観測期間中に消滅しなかったものも多数)
ともあれ,
おおざっぱな解析から.
「調査終了の xヶ月前に出現した n0 枚の葉っぱが終了時点では n1 枚になった」
ということはわかっているので,
xヶ月生残する確率を logit モデルで近似的に説明してみましょう,
と.
つまり個体差・樹種差はいったん無視して glm()
を適用.
-
説明変数をふやしていくと
……
LMA・重量あたり窒素・生活形
(樹木・草・つる植物・シダなど)
がモデル選択で残った.
よくわからんけど,
LMA だの窒素だのは値が大きければ長命化,
という方向で.
ふーむ.
個体差とか考慮するともうちょいモデルが単純化されるんではないかな.
あと,
死にかけ個体からのサンプルは葉っぱも死亡確率が高くなる,
という偏りがあるとわかった.
-
熱帯葉っぱ問題がひとまず片づいてから Dell 機にもぐりこんでみたら,
屋久島葉っぱ問題「窒素ぬき」版の計算が終了していた.
50 MCMC step とばしサンプリング.
うん,
窒素量と称されている観測値は
このデータに見られる葉っぱの死亡確率を説明するのに
何の役にもたってない,
とわかった.
窒素ぬきモデル
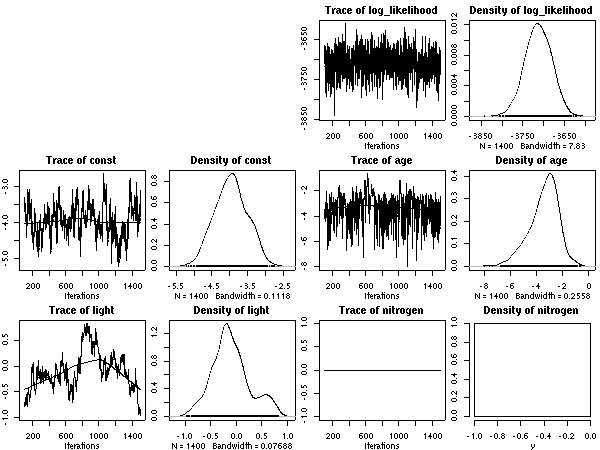
[窒素ぬきモデル]
上の図の nested parameter 図で窒素パラメーターの事後確率分布は
R
の
density() 関数がゼロデータからでっちあげたもの.
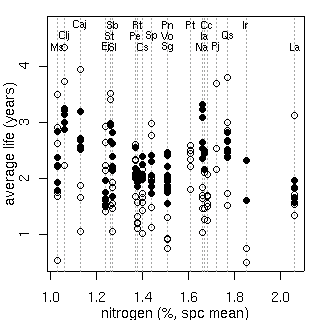
左の図は「平均寿命と葉内窒素量」の関係
(樹木個体ごとに計算して推定平均葉寿命の単位は年,
葉っぱ内の窒素量種内平均値の単位は重量パーセント).
昨日の図
とほとんど変わらん.
つまり窒素を説明変数に使わなくても平均寿命の計算はできて,
しかも (種差があるようにも見える)
窒素量とは無関係,
ということ.
後記:
ここで図示してたのは平均葉寿命 (死亡時葉齢の平均値ではなく)
平均葉齢だった
……
訂正版は 15 日に.
-
さすがに,
この問題もだいたい一件落着してきたな.
-
2040 研究室発.
買いもの.
北海道の野菜不足,
いよいよ深刻.
2110 帰宅.
晩飯の準備.
晩飯.
-
来週木曜日の東京出張の準備なにもできとらん
……
ふーむ,
近ごろは
LaTeX beamer
とゆーのがはやっているのか.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0930):
食パン.
- 昼 (1350):
米麦 0.6 合.
麻婆豆腐.
- 晩 (2230):
米麦 0.8 合.
ダイコン・ニンジン・ネギ・煮干の味噌汁.
2006 年 01 月 15 日 (日)
-
1010 起床.
よく眠れたけど生活周期がずれるのはまずい.
朝飯.
コーヒー.
洗濯.
怠業.
研究室ネット雑用など.
-
1305 自宅発北大構内走.
曇天.
「屋久島計算,
修論しうたうけ部分はひとまず終わったなあ」
とりらっくすした状態で脳を振動させつつ走っていると,
いくつかのことに気づいた.
-
ひとつはちょっとした計算ミス.
昨日・一昨日の図で「平均葉寿命」となっていたのは「平均葉齢」だ.
両者の違いは
-
平均葉寿命: 葉っぱ死亡時点での葉齢の集団平均
-
平均葉寿命: 生きてる葉っぱの齢の集団平均
あとで修正しとかんといかんね.
-
Nested かつ階層ベイズなモデリングについては課題山積のままだな,
と検討しつつ
1400 帰宅.
体重 73.2kg.
昼飯.
-
1600 自宅発.
曇.
1620 研究室着.
-
まずは平均葉齢ではなく平均葉寿命
(死亡時点の平均葉齢)
を計算するようにプログラム修正.
左が新しく計算しなおした平均葉寿命,
右は
一昨日
に計算した平均葉齢.
まあ,
点の相対的な位置はそれほど変わらんわけで.
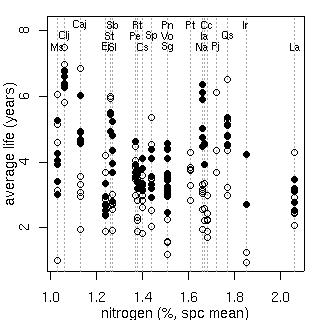

-
牛原さんが来てたので上の計算結果を納品する.
-
A801 機にも「念のため」検算させといたジョブも,
とっくに終了している.
窒素の効果ナシ,
という順当なもの.
モデルは窒素項あり,
100 MCMC step とばしのサンプリング.
-
昨日は「なンで窒素が効果ナシだったり長命化になったりするんだろう」
と困っていたわけだが
……
こういうふうに 22 樹種をつきまぜたデータセットに対して
MCMC 計算による階層ベイズモデルの推定やったりすると,
(おそらく初期値の与えかたによって)
途中でみょーなところに「ひっかかって」自力では脱出できなくなるのだろう.
これを回避するには拡張アンサンブル法といっても
パラレルテンパリングしか知らないんだけど,
こういった方法で「にせピーク」から脱出させるしかあるまい.
-
パラレルテンパリング法について伊庭さんからメイルで
ご教示いただいたんだけど
……
今月はじめに私が試験的に実装してたのは
高温・低温ふたつの系列つかったケチな計算だったわけだが,
実用的には十段二十段ぐらいは準備するものらしい.
まあ,
たしかにそれぐらいないとうまく動かないような気もする.
-
spam 近況.
私あてに毎日 50-60 通ぐらい spam メイル送られてくる.
これのたいはんは
Gmail
でブロックされて手もとにはとどかない.
しかし,
これだけの数になると毎日 4-5 通ぐらいは「すりぬけて」くるんだよね.
もちろん手もとの計算機に構築してある最終防衛ライン
spamassassin
でほとんどゴミ箱おくりになっているんだけど.
-
一時間弱ほどかけて実吉さん発芽データ変換.
このデータ変換作業もこれにて終了,
か?
-
東京出張の準備によーやくとりくむ.
まずは苫小牧でんどろモデルの説明の圧縮.
-
なかなかススまん.
2100 研究室発.
2115 帰宅.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (1030):
バゲット.
- 昼 (1440):
タラコスパゲッティー.
- 晩 (2230):
米麦 0.8 合.
ダイコン・ニンジン・ネギ・煮干の味噌汁.
2006 年 01 月 16 日 (月)
-
0800 起床.
朝飯.
コーヒー.
なぜか
adaptive rejection sampling
のアルゴリズムに没頭してしまう.
現実逃避の一種だろう.
0955 自宅発.
雪.
1010 研究室着.
-
木曜日の東京出張の準備,
ぢりぢりとススめる.
-
Vine Linux 3.2 から
TeX & LaTeX package が
tetex-2
になっているんだけど,
こういう指定では
\newcommand{\latinname}[1]{\textit{#1}}
...
\PurpleBox{推定結果: イタヤカエデ \ (\latinname{Acer mono})}
学名の部分がイタリックにならない
(tetex-1 Vine 版では OK だった).
理由は日本語フォントにはイタリックはありえない,
というところだろう.
イタリックがダメなら斜体と指定すればいいのかといえば,
そうでもなかった.
そこで姑息な回避わざとしては,
\newfont{\FONTi}{cmti10}
\newcommand{\latinname}[1]{{\FONTi #1}}
...
\PurpleBox{推定結果: イタヤカエデ \ (\latinname{Acer mono})}
というのが使える.
-
昼飯.
-
投影資料,
あいかわらず LaTeX の
\documentclass{seminar}
で作って,
dvipdfmx
で PDF ファイルにしてるんだが
……
ファイルサイズが大きくなりがちである.
たいして重い図があるわけでもないのに 1MB 超えた.
画像ファイルのとりこみには
jpeg2ps
いるのだが.
-
ちょっと調べてみると
……
pinna works
で紹介されている
PNG/JPG/PDFを取り込む
ってのが良さそうかな.
ebb foo.png
で
\includegraphics{foo.png}
すればよい.
なぜかしら
jpg ファイルにはこの方法が通用しない
(「ニセ情報です」とエラーがでる).
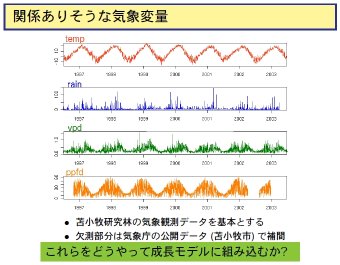
[ということで]
作図プログラムなどもあれこれと作り直し中.
ebb
使った方式だとファイルサイズは小さくおさえられるんだけど,
xdvi
できなくなる
……
ので
make で PDF ファイル作り,
xpdf (reload 使える)
を previewer にする.
-
うだうだと作業を続けるのがイヤになってきたので撤退.
1930 研究室発.
1955 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0820):
米麦 0.7 合.
ネギ卵炒飯.
海藻スープ.
- 昼 (1305):
研究室お茶部屋.
米麦 0.5 合.
ダイコン・ニンジン・ネギ・煮干の味噌汁.
- 晩 (2140):
米麦 0.7 合.
ハクサイ・ニンジン・ジャガイモ・ネギ・ブナシメジ・
タラすりみのシチュー.
2006 年 01 月 17 日 (火)
-
0730 起床.
朝飯.
コーヒー.
0910 自宅発.
雪.
0925 研究室着.
-
また東京出張の準備.
-
1030-1140
研究室セミナー,
本日は西村さんでサロベツ湿原の地表 (植生)
と地下 (地下水) について.
データ構造がややこしくて,
発掘年 - 調査年 - 季節変動 - 空間相関
……
とあれこれ交絡していて,
ですね
……
-
東京出張の準備.
屋久島葉っぱ調査の方法について
いまさらながら牛原さんにあれこれとお尋ねして,
うるさがられる.
-
CANON LBP-2810 (カラーレイザープリンター)
用の再生トナー 3 本で 58275 円.
高い.
しかし予算消化雑務はつづく.
-
昼飯.
窓の外の雪は
……
けっこう降っている.
-
松田さんと,
とある論文で使っているアヤしげな分散分析について検討する.
著者がまちがってるか情報を隠匿してるかのどっちか,
ではなかろーか.
私が参加できないしあさっての
論文セミナー
のものなんですが.
-
進化植物学研究会担当の庄山さんの圧力に負けて
進化植物学研究会 web page
本年ぶんを作る.
-
出張準備のつづき,
いきづまると A 棟 8F 内をうろうろする
……
をひたすら繰り返す.
-
2200 ひととーり,
できた.
-
2215 研究室発.
雪.
2230 帰宅.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0810):
米麦 0.5 合.
ハクサイ・ニンジン・ジャガイモ・ネギ・ブナシメジ・
タラすりみのシチュー.
- 昼 (1310):
研究室お茶部屋.
米麦 0.5 合.
ハクサイ・ニンジン・ジャガイモ・ネギ・ブナシメジ・
タラすりみのシチュー.
- 晩 (2240):
米麦 0.7 合.
ハクサイ・ニンジン・ジャガイモ・ネギ・ブナシメジ・
タラすりみのシチュー.
2006 年 01 月 18 日 (水)
-
0920 起床.
また生活周期がずれた.
朝飯.
コーヒー.
1035 自宅発.
雪.
1055 研究室着.
-
出張準備のほうはひとまず片づいたので,
来週の月曜日・水曜日の統計学授業の準備.
お題としては,
一般化線形混合モデル (generalized linear mixed model; GLMM)
のハナシをしたい.
というのも,
たいへん利己的な理由ながら,
3 月の自由集会
に使いまわせるからだ.
-
蛇足ながら私がいつもにもまして露骨に利己的である理由は,
「今年度の統計学授業
はもうやってしまった」
つもりになっていたのに,
さらに二回ぶんも追加されてしまったためである.
-
しかしながら (受講者の大多数をしめる) M1 あいての
90 分 × 2 回を
GLMM ハナシばかりでうめつくすのはちょっとしんどい
……
ハナシをさせられるほうも,
それを聞かされるほうにも.
したがって,
水曜日 90 分間を GLMM 予想脱落者数多数まにあっくハナシをやることにして,
月曜日はその「準備」みたいなものにあてるか.
となると,
ふつーの logistic 回帰とかポアソン回帰つまり
GLM (generalized linear model) の説明,
とか?
-
とりあえずまた LaTeX ファイルの準備.
-
昼飯.
窓の外は大雪.
甲山さんは
「明日の東京出張の飛行機,
とぶんだろうか?」
と心配してる
……
えー,
私の東京出張は甲山さん主催のぷろっとねっと会議でハナシをさせられるため,
なんだよね.
で,
新千歳空港の滑走路に明朝 3m 積雪したがゆえに
東京出張キャンセルになっても当方にはまったくもって何も不都合ない,
と考えている自分を発見する.
-
残念ながら,
札幌から JR で 40 分ほど離れた千歳市に
北海道玄関的な飛行場が建設されたのは,
「札幌に比べて雪がつもらないから」
という理由があるからなんだけど.
最深積雪量は
千歳市 0.5m ぐらい,
札幌市 1m ぐらい.
この量は一日で最も多く雪が降った日の降雪量なんで
極値 (extreme values) ではあるけれど.
年間の累積だと千歳市は 1.5m ぐらいで,
札幌市は 5-6m (!) ぐらい
……
とのこと.
-
で,
うだうだと授業準備
……
ススまん.
-
イヤになるとまた A 棟 8F 内うろうろして,
院生たちにイヤがられてみる,
と.
-
授業につかう架空例,
とりあえず乱数を組み合わせていろいろとこしらえてみる
……
ふーむ,
「個体差」ありデータに対する
混合モデル使った推定は結果を単純化させるのか複雑化させるのか?
授業で使うような単純化された架空例の場合だと,
要因の効果をきわだたせるような推定値を出すな.
それに対して,
実データでパラメーターたくさん推定させるような場合だと,
「個体差」は「そんなにたくさんパラメーターいらんでしょ」
という方向でモデルを単純化させる
……
というこうとかしらん?
-
混合モデルによる推定結果が「要因の効果をきわだたせる」
例みたいなものを示すために,
「個体差なし」の
glm()
と「あり」の glmmML() を対戦させて遊んでみる
……
ふーむ.
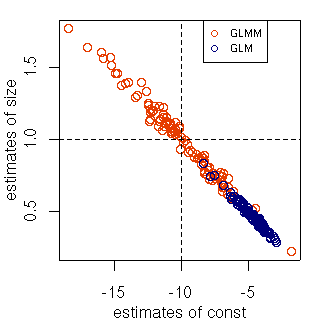
[glm() vs glmmML() 百番勝負]
glm(y ~ 1 + size, family = binomial, ...)
といった計算で得られる推定値.
ホントの値は十字線交点 {-10, 1}.
標本
y は二項乱数
rbinom()
で生成.一個体から 10 反復,100 個体.
キツい「個体差」あり
……
ということで,
当然ながら
glmmML()
のほうが良い推定値を出しているように見える.
glm() のそれは明らかに偏る
……
となるようにこの例題は作ったわけだが.
授業に使えるか?
しかし,
この
glmmML()
のばらつきのすごさよ.
-
ついでながら
……
線形モデルのたぐいでは,
上の図で示されているように,
推定値間に強い相関が生じる.
これを誤解して
「パラメーター a と b のあいだで
ゆーいな『とれいどおふ』が発見されました」
とか発表しているまぬけなヒトがいたりするけど,
こんな「関係」に「生物学的意味」とやらは何もない.
-
2010 研究室発.
雪はやんだ.
2030 帰宅.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0950):
米麦 0.7 合.
麻婆豆腐.
- 昼 (1420):
研究室お茶部屋.
米麦 0.5 合.
麻婆豆腐.
- 晩 (2130):
米麦 0.7 合.
麻婆豆腐.
ホッケ電磁波酒蒸し.
2006 年 01 月 19 日 (木)
-
0700 起床.
ねむい.
コーヒー.
朝飯.
-
出張とかめんどうだな
……
と汽車の時刻など調べてみると,
まだまだよゆーある.
ということで洗濯.
ついでに本日の「ちゅーとりある」内容のみなおし.
-
0910 自宅発.
晴.
0917 JR 札幌着.
いやはや,
雪ふってるわけでもないのに空港いき快速エアポート 15 分の運行おくれ.
0927 同発.
1005 新千歳空港着
……
うーむ,
飛行機の運行も 20 分おくれ.
冬の北海道はかくのごとく天気が特に悪くなくても
旅程に時間のよゆーが要求される.
1048 ANA56 便 B747-400 搭乗.
1110 離陸.
機中,
本日のハナシのみなおし.
1225 羽田空港着陸.
1242 ひさしぶりに東京モノレイルにのって同発.
1308 JR 浜松町で乗り換えて,
1314 JR 東京着.
ここまで620 円.
丸ノ内口からでて神田方面に 10 分ほど歩くと,
本日の PlotNet 会議場である
三菱総研
(浦口さんの職場) 着.
-
2F 会議室にいくと清野さんたちがすでの到着.
昼飯.
-
1400 すぎから PlotNet 会議.
甲山さんが 15 分間ほど趣旨説明.
そのあとチュートリアル的なハナシということで,
苫小牧の中村さんと私が 1.5 時間ほど.

[ぷろっとねっと会議]
なンというか甲山さん関係者のあつまり
(参加者数 20 名ぐらい),
というような
……
plot 研究者集団の齢分布は「高齢化」しつつあるそーです.
つまり若者がいない.
-
中村さんは環境省がカネとか出してる「モタリング 1000 (もにせん)」
傭われなので,
そのそのあたりの進捗状況の報告を.
佐渡ヶ島ははずれ地であるだけでなくはずれ値だとか,
地表徘徊性「甲虫」は個体数・多様性ともに「北」のほうが多いかも,
というような
……
-
で,
私は鍋嶋さん・日浦さんとススめている苫小牧でんどろモデリング,
そして牛原さん・甲山さんとススめている屋久島葉っぱ寿命モデリング.
どちらも生物学的におもしろい部分は今回はわきにおいて,
そういう結果を出すための統計モデリングのハナシに集中する
……
といってもデータをどうとらえたらよいのか,
という「考えかた」の説明に終始したわけだが.
なぜ PlotNet と関係あるのかというと,
同じ個体から何度も何度もデータを測定する場合の「個体差」のあつかい
(苫小牧モデルの一般化線形混合モデル),
多樹種だけど各樹種の標本数が必ずしも多くない場合
(屋久島モデルの nested & 階層ベイズモデル),
ってのがまさに毎木調査データでもよく出現する問題であるからだ.
-
質疑応答もいろいろと.
今回はどちらのモデルにも random effects
と呼んでよい要因が入ってるんだけど,
これを「個体差」と名づけて説明するときは注意せんといかんね
……
ってのも「サイズ」みたいな fixed effects も個体差ぢゃないの,
と疑問におもうヒトもいるからだ.
うーむ
……
fixed effects だの random effects だのを最初にもちだしてみて
(何が fixed で何が random なのかいつでもモメるわけだが),
後者をここでは「個体差」と呼ぶことにします,
としてみるかな.
-
苫小牧モデルは「個体差」を図示しやすく,
屋久島モデルは図示にかなり工夫が必要である.
-
あとは PlotNet 会議.
浦口さんによるデータベイス準備の説明,
さらに甲山さんの事務雑談.
私は部屋の片隅でこそこそと来週の授業の準備してたら,
いつのまにか甲山さん思いつき雑用を押しつけられそうになっている
……
なんとか逃れよう.
-
1800 すぎ終了.
このビル B1F 居酒屋ふうなところで懇親会.
目の前に日浦さん・浦口さんが座り,
苫小牧の論文分担部分はやく書いてくださいってことだよとか,
鍋嶋さん困らせてないでしょうねとか
キビしく追及をうけたので逃げる
……
さっさと授業の準備を終わらせて,
とりくまねば.
あ,
しかし日曜日はセンター試験監督とかあったな.
-
2000 ごろここは撤収して,
東京駅方面で二次会みたいな.
-
2250 宿
着.
部屋はやや広いけど値段たかい東横イン,
みたいなかんぢ.
まあ,
PlotNet 予算から出してもらっているんだけど
……
-
昼間の発表やったときにうけた質問,
だいたいは思い出せるんだが,
何点かおもいだせん
……
ということで,
眠いのになかなか寝つけなかったり.
時刻はすでに 2500 すぎ.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0730):
米麦 0.7 合.
納豆.
- 昼 (1350):
三菱総研 2F 会議室でこんびに握り飯.
- 晩 (1830):
三菱総研 B1F 居酒屋,
など.
2006 年 01 月 20 日 (金)
-
0700 起床.
東京大手町の宿.
飛行機出発まで時間あるけど,
こんな都心部にいてもやることないので,
さっさと撤収することに.
宿 1F で無料給食やってるんでそこで朝飯.
このあたりも東横イン的だな.
よく知らないんだけど,
最近のびぢねすホテルとやらは全部こうなのか?
東横インだと「型ぬき」握り飯 + みそ汁 or バターロール + コーヒー,
ここは安そうなパン三種 + ぬりもの + サラダ + ゆで卵 + コーヒー.
0740 チェックアウト.
一泊 10350 円 (!),
まあこの値段なので朝飯にも原価で
150 円ぶんぐらいの上積みしてますってことだろう.

[大手町]
左から昨日の会議場所の三菱総研,
日経新聞本社,
経団連会館.
東京駅にむかう途中
ここ
からの南方の視界なんだけど,
地図みたら JR 神田にいったほうがよっぽど近いぢゃん.
いやはや.
-
0801 JR 東京駅発.
0806 浜松町で東京モノレイルに乗り換え.
ここまで 150 円.
ここから 470 円.
0812 同発の 0837 羽田空港第二ターミナル着.
ここでチェックインしてみると,
予定より一時間早い便である 0900 発に乗れそうなんでそちらに変更.
-
すでに搭乗がはじまってるので急ぐ.
こういうときにかぎって,
ですね.
私はカバンの中とかに検問でひっかかるモノはいれないように注意してるんだが
……
近ごろの荷物チェック流行はなんと「ツメ切り」.
二度にわたる X 線照射ではツメ切りを十分に破壊できなかったとのことで,
ツメ切りだせと命じられた.
動作緩慢なる係員あれこれとひねくりまわしたあげく,
これは航空テロ犯たちが愛用している
大量殺戮型ツメ切りとはいささか異なるタイプらしいとの見解に到達したよーで
……
よーやくのことで釈放された.
-
今日の運動: 羽田空港第二ターミナルビル走 300m,
荷物つき.
-
0857 ANA 55 便 B747-400 搭乗.
今日は最後尾の席にしてみたんだけど,
このあたりは人口密度が少なくていいね.
0918 羽田空港 C 滑走路を南→北と離陸.
晴.
すでにばてぎみ.
1026 新千歳空港着陸.
1051 快速エアポートで同発.
1131 札幌着.
ここまで 1040 円.
本日も 5 分おくれぐらいで運行中.
1145 研究室着.
ばてた.
-
ばてつつ昼飯.
-
鈴木牧画伯が
イヌ植物だじゃれ年賀状
公開しておられる.
牧さんわーるどというかんぢで良いですよね.
-
とーとつに
R
のハナシ.
lmer()
という GLMM solver が
Matrix
package 内に入ってるな.
挙動を調べてみなくては.
しかし,
ここに書いててもどわすれしそうだ.
-
900 億回
乱数を発生させる必要のある計算に一時間ぐらいかかるんだけど,
もっと速くなる計算アルゴリズムない?
との質問くる.
そんなのあるわけないぢゃん.
乱数発生だけでも一秒間に 2500 万回になる
……
ホントに一時間で計算できてんのか?
-
と思ったら,
ぢつは私の ThinkPad X31 (Pentium M 1.6GHz) ですら 1 秒未満で
1000 万個の乱数を発生させることができた.
R
で調べると,
> system.time(runif(10^7, 0, 1))
[1] 0.97 0.11 1.08 0.00 0.00
とすると 900 億個だと 150 分間か.
ところが,
ここで単純に R で一億回乱数発生やらせると,
> system.time(runif(10^8, 0, 1))
[1] 20.06 8.43 55.26 0.00 0.00
10 秒ではなく 20 秒かかる.
これは計算結果格納 vector のメモリ確保とかに時間くっているのか?
-
ところで,
そんなに莫大なる個数の乱数発生させるならちゃんとした
擬似乱数
発生法つかってるんでしょうね
(R の場合は
めるせんぬついすたー)
……
-
ふーむ,
多項版の超幾何分布は
The Multivariate Hypergeometric Distribution
とゆーのか.
-
などとうだうだやってて,
来週の授業の準備はススまず.
1855 研究室発.
1910 帰宅.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0720):
宿の無料給食.
- 昼 (1250):
研究室お茶部屋.
こんびに握り飯二個.
- 晩 (1940):
食パン.
ハクサイ・モヤシ・エノキダケ・卵の炒めもの.