ぎょーむ日誌 2006-01-12

2006 年 01 月 12 日 (木)

• 0700 起床． 朝飯． コーヒー． 洗濯．
• 昨日からつづけている隠れ計算 (hyperspecies の層において事前分布を無情報化する)， ひと区切りついたのでここに記録しておく． まずはシュート伸長の休眠・二度伸びの確率モデル． 10 MCMC step とばし． これは (データが単純なので) どういうふうに計算してもあまり変わらない．

シュート伸長の休眠・二度伸び

• つぎに葉っぱ死亡確率のモデル． 50 MCMC step とばし． これにはふたつあって， まずは

  1 + 葉齢 + 明るさ + 窒素

  つまり「明るさが葉っぱ死期を早める (あるいは遅くする)」 モデルから．

シュート伸長の休眠・二度伸び

葉面積あたり窒素量モデル (これはかなり LMA に近い量)

葉重量あたり窒素量モデル

• つぎは

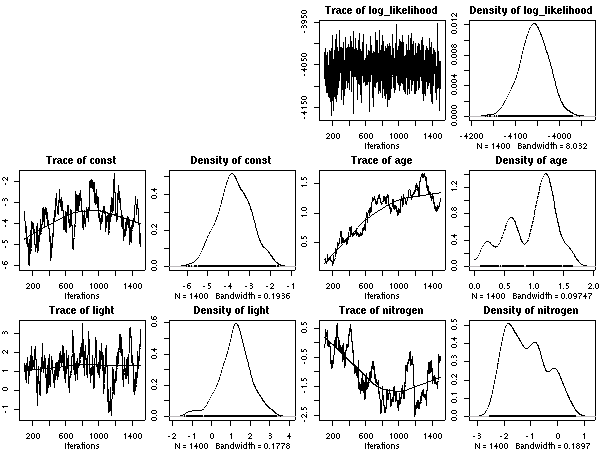
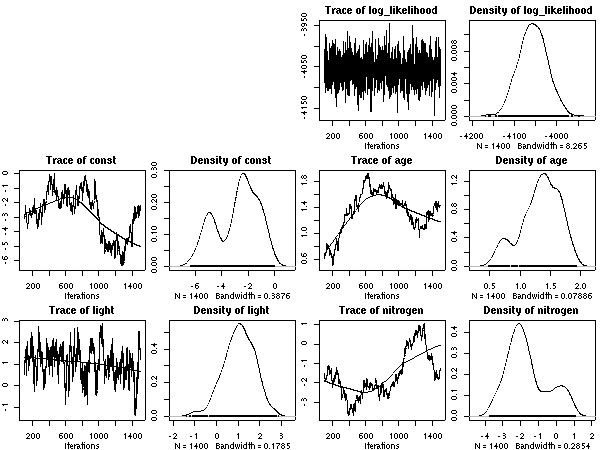
  1 + (1 + 明るさ) × 葉齢 + 窒素

  つまり「明るさが葉っぱ『老化』を加速する (あるいは減速する)」 モデル．

葉面積あたり窒素量モデル (これはかなり LMA に近い量)

葉重量あたり窒素量モデル

• 現時点でだいたいわかってきたことは ……
  • 葉っぱの一年間の死亡確率は定数ではなく， 葉齢に依存して上昇する． 樹種によってはこの値が極端に高いものがあり， これは明るさなど他の要因とはあまり関係なく， 短期間のうちに葉っぱを脱落させる樹種である．
  • 明るい場所では (だいたいにおいて) 葉っぱの「老化」 (ここでは葉っぱの死亡確率が高くなること) の開始が早いもしくは老化が加速している (葉齢にともなく死亡確率の上昇が大きくなる)． しかしながら， そうでない樹種もいるので， 明るさ依存性のばらつきは大きい． 後述する窒素との交絡もある．
  • 重量あたり窒素量は (おそらくノイズが多いため) 影響がよくわからない， あるいはモデルによっては葉っぱの老化開始を遅くしている． しかしながら， モデルによってはばらつきが大きい． その原因はふたつ考えられる． ひとつは樹種によっては窒素が老化時期を早めている 可能性があるため． もうひとつは， 樹種によっては「明るいと窒素が多い」 という交絡があり， 「明るさ」を窒素量で代用できる場合があるため (パラメーターの遷移をみていると， 明るさと窒素の変動には負の相関がある)．
  • 面積あたりの窒素量 (これはほとんど LMA に近い) の影響もよくわからない， あるいはモデルによっては葉っぱの老化開始を遅くしている．
  まあ， これぐらいはこれまでの計算結果から言っていい範囲だと思う．
• 「樹種差」なるものを random effects とする 今回の新しい試みの利害得失はどんなものかしらん． この屋久島データみたいに， 多樹種 (22 樹種) で樹種ごとの標本数が少ない (各樹種最大 12 標本しかない) という状況ではこれしかパラメーター推定の方法はなさそうだ (このあたりもうちょいよく考えてみたい)． しかしながら同時に， 「樹種差」なるものの変化があまり「連続的」ではない場合， hyperspecies の層において事後分布は「多峰的」になってしまう．
• そしてこのように単純にベイズモデル化したところで， 交絡 (confounding) の問題が自動的に解決するわけではない． パラメーターの遷移をみることで， 「あ， 交絡してやがるな」 というのがわかりやすくはなったけれど．
• ところで書き忘れていたんだけど …… いつも割り算値をイヤがっているぎょーむ日誌で割り算値記述がまちがっていた (訂正の文を二日前に追加しといたんだけど)． ここでいう「面積あたり窒素量」なる数量は，

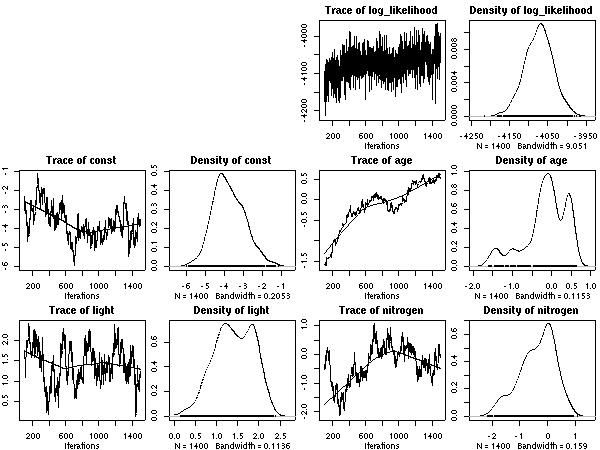
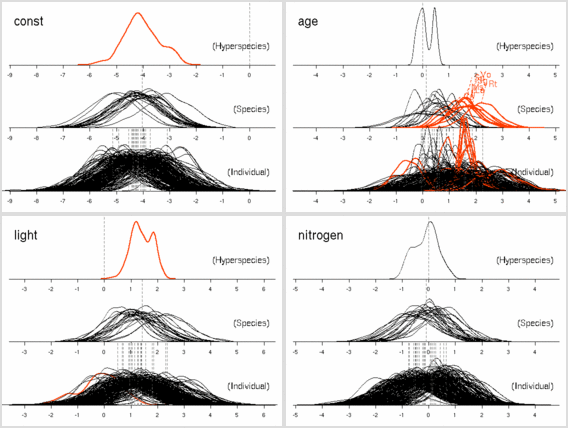
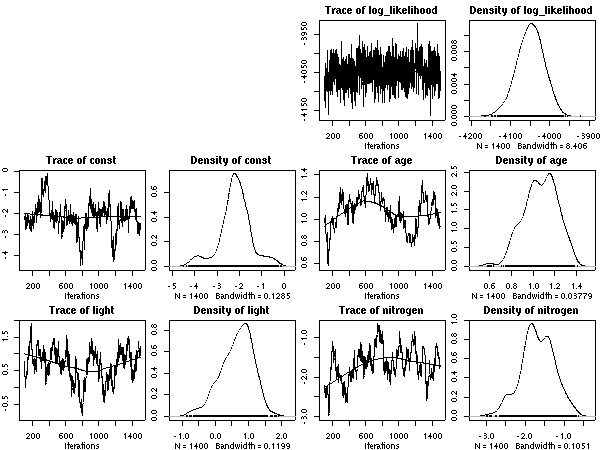
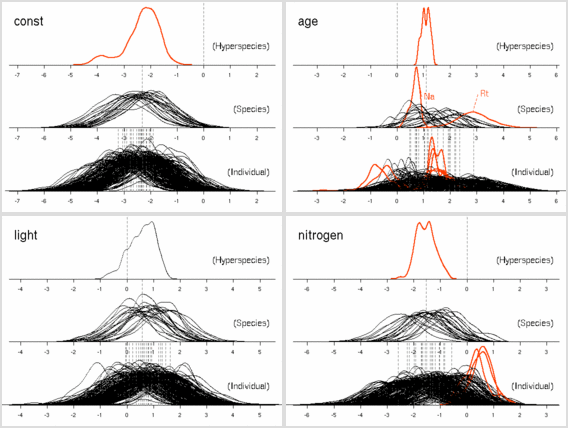
  重量あたり窒素量 (これは測定機械が吐きだす割り算値)
    × LMA (これは人間が計算した割り算値)

  で計算している． 計算プログラムの中ではそうなっていたんだけど， ここに書いたときには LMA でわることにされていた． 嗚呼．
• 1030 自宅発． 雪． 1045 研究室着．
• ここまでの計算結果， いろいろと検討してみる …… 計算改善アイデアもつきてきた． まあ， こんなところなのかな．
• ふと， species の層において分散逆数は種間で共有するけれど 平均は樹種ごとに異なるガウシアンな事前分布としてみたら …… とゆー夢想にとりつかれてしまったんだけど， これ以上滞納してたら計算発注者に見つかって怒られそうなんで， ここまでの結果から 寿命分布など計算するプログラム作りフェイズに移行していく．
• そういや， 来週の東京出張の準備はまだ何もしてないや． そのあとの M1 授業の準備も． 気が重い．
• A 棟 7F の愛煙家某先生からのメイル．

  喫煙は、平均寿命を縮める。よって、他の死因の発生確率が下がる。例えば、喫
  煙者は、交通事故による死亡率は非喫煙者より低くなる。よって、喫煙は交通事
  故による死亡率を下げる(良い)効果がある。なお、「交通事故」の部分は、他の
  事故名や喫煙とは無関係の病名に変えても良い。
  んー。そうだったのか。
  

  私の返信．

  喫煙者は注意深くて，非喫煙者より交通事故にあう確率が低い，と仮定してみ
  ましょう．この場合，交通事故にあう確率が低くなることで，そのぶん喫煙に
  よって死ぬ確率が高くなってしまいます．おそろしいことです．
  喫煙者は喫煙による死亡確率を下げるために，より不注意になって頻繁に交通
  事故を起こして交通事故で死ぬ確率を高めるべきです．
  

• 昼飯調達のため北大生協へ． 吹雪． 研究室にもどって昼飯． 時刻はすでに 1500．
• (膨大な量になる) 推定結果と観測データを対応づけるいろいろな R プログラミング．
• 1930 ごろひととーりできた …… が， これがじつにじつに驚くべきものばかり． 階層ベイズモデルだのマルチレイヤーモデルだのの理解がまだまだだ， というのがわかった． うん． 計算あれこれ全部やりなおしだな．
• とりあえずモデルは

  1 + (1 + 明るさ) × 葉齢 + 窒素

  で計算してみる．
• パラメーター推定の結果との食い違いが一番いちじるいしいのはココだ …… 個々の個体ごとに特定されるパラメーターから計算した 平均葉寿命と重量あたり窒素量の関係はかくのごとし． あたかも窒素が多いと短命であるかのように見える． あとで説明するように， これは「明るさ」との交絡なのである (明るいところ: ○)．

[推定平均葉寿命 vs 窒素量]

推定平均葉寿命の単位は年． 葉っぱ内の窒素量の単位は重量パーセント． あとで説明するように， いくつかの個体では「齢」依存性パラメーターが負になっているので， ここではそれをゼロとおいて計算している．

• Hyperspecies と species の層においては nitrogen のパラメーター推定値は ほとんどマイナスの値になるのにもかかわらず， なぜ上のように見える図ができてしまうのだろうか? じつは樹木個体のパラメーターにおいて「調節」がなされていた．

[窒素パラメーター vs 窒素量]

縦軸がパラメーター事後分布の平均値． 窒素量が少ないほど値が低い (長命化) と推定されている． こういう個体の窒素量に引きずられた推定結果が妥当なのかどうかは， あとで検討してみる．

• こういう関係があると， 当然ながら線形予測子の部品としては 「窒素」コンポーネントは 下の図のごとく「ノイズ」に近い …… つまりこのベイズ推定で 「モデル選択」ができていれば削除されるような要因なのである．

[のいず]

縦軸は個体ごとの窒素パラメーターとその個体の窒素量の積． この図は何を表しているかというと， 窒素量の大小は葉っぱ死亡確率に何の影響もおよぼさない， ということ．

• じゃあ， 何で nmass とやらの大きいところで早死にしているかといえば， 明るい場所だから， ということになる．
• つまりまとめると，
  • 全個体の窒素量 (nmass) の勾配は 死亡確率の大小と対応しない (上の「のいず」図)
  • 明るい場所では葉っぱは早死にする
  • 葉内の窒素が極端に多い (2% より大きい) 場合， それは明るい場所に限定される
  • 窒素が極端に多い場合に早死にしている理由は 「明るいから」とするほうが妥当である
  ということ．
• いやー， いろいろと検討すべきことがあるな ……
• まずは窒素まわりで残された問題からいこうか． ここで問題なのは， hyperspecies - species - tree の層において， hyperspecies - species までならば明らかに 「窒素が多ければ死亡確率は低下」に見えた現象が， 個体内での補正 (上の図) とでも言うべきパラメーター推定によって， 「窒素と死亡確率は無関係」 となったことだ．
• これは (このモデルのもとでは) 窒素はほとんど死亡確率を説明できない， という結果を階層間のややこしい調節で実現してしまったんだろうな． すると なぜ hyperspecies - species ではマイナスになったのだろうか? ゼロを中心にして反転した結果でもさしつかえないように思える． これは「明るさ」との交絡のせいではないかな． つまり， 窒素のほとんどの値域では相関ナシでもよいけれど， 右端の窒素が極端に多いところでは高い値であってほしい， と．
• 実際のところ (上の比較では使っていないほうのモデルである)

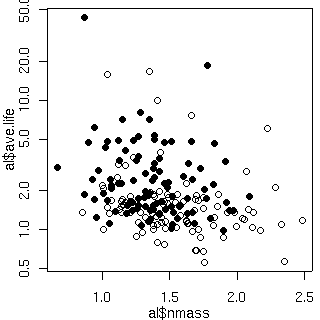
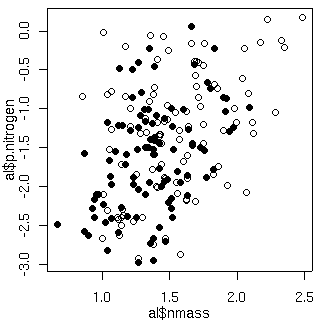
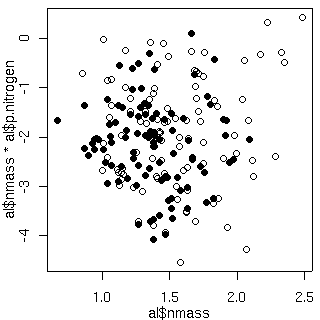
  1 + 葉齢 + 明るさ + 窒素

  モデルのほうではしょっちゅう 「ゼロを中心にした反転」が発生していたわけで．
• このあたりすっきり解決するためには， モデル選択が必要かな． べいぢあん世界でのモデル選択となると， またいろいろと勉強してプログラムをかなり改造せんといかんような気もする …… これの検討はいったんおく．
• 他にもいろいろと問題ある． たとえば齢依存性だ． これは自由に選ばせたらダメだね． 「全体的にはプラス」であっても個体の中には マイナスの値をとるやつがでるからだ． 「生き残るほど死亡確率が下る」 というすっとぼけた個体がいたっていいぢゃん， と気楽にかまえていたんだが …… というのも x 才までに死ぬ確率は単調に増大していくだろう， などと思いこんでいたわけなんだけど， 実際はそうではなかった． ある齢から確率 1 で生きのびるやつもでてきた． いやはや．
• 解決策としては事前分布を変えるしかない． 葉齢にまつわりつくパラメーターは常に非負の値をとる事前分布を使う， と．
• モデル選択はあとまわしにして， とりあえずこのへんからとりくんでみるか． あるいは事前分布を変えるのではなく， ガウシアン事前分布から生成されたパラメーター p を exp(p) として使う， とか?
• ものの試しとて葉齢まわりに exp() かませる試運転 …… ふーむ， まあしばらく放置．
• 次に個体ごとに窒素パラメーターとかを自由に選ばせてよいのか， という問題だよな． 面倒なことはやめてモデル選択でケリをつけるのか． それとも， モデリングでもう少し工夫すべきなのか．
• 時刻はすでに 2210． 晩飯でも調達するか． 年末に 北 11 西 4 に新しくできた Sunkus までふらふらと． 研究室にもどって晩飯．
• 応急処置的な対策として， 窒素量を全部種内平均値に置き換える， という方法を採用することに． というのもここで興味あるのは種内差ではなく， 窒素量の種間差が葉っぱ生き死ににどう関与するか， を明らかにすることだから， というような理由になるか． Hyperspecies - species - tree の各層に Replace_nitrogenSPC() なるメソッドを追加してみる．
• そういや甲山さんが「(窒素量の) 種内差と種間差は意味が違う」 と言ってたのはこういう意味だったのかなあ．
• 試行錯誤で関数型など変えつつ試験運転つづく． 上で

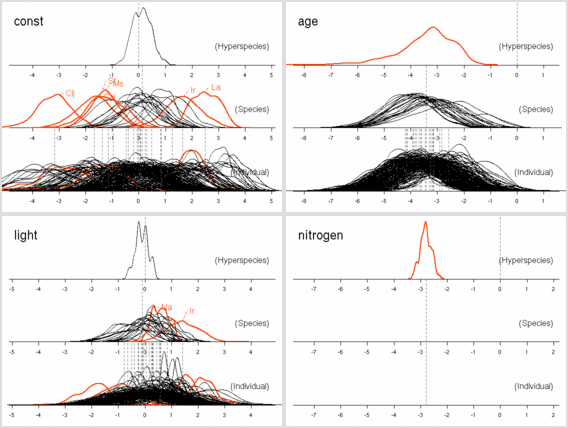
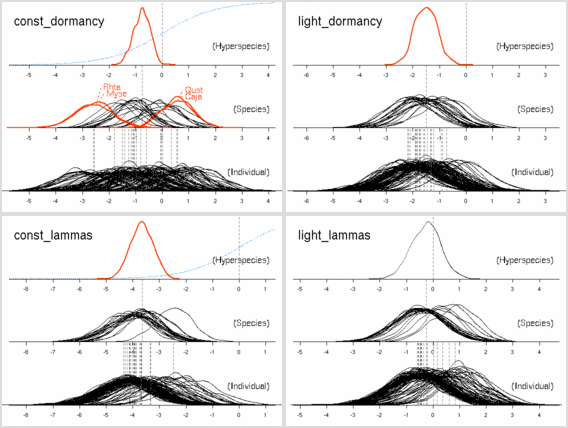
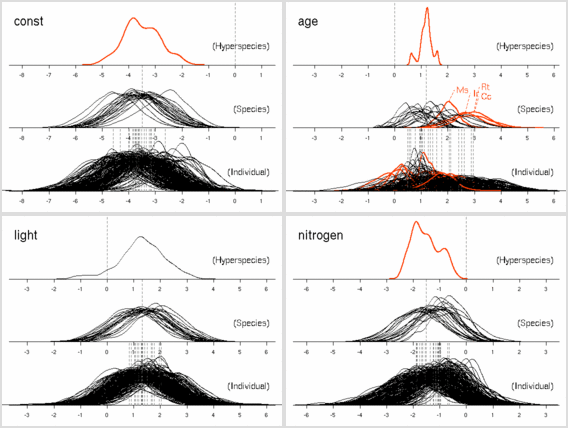
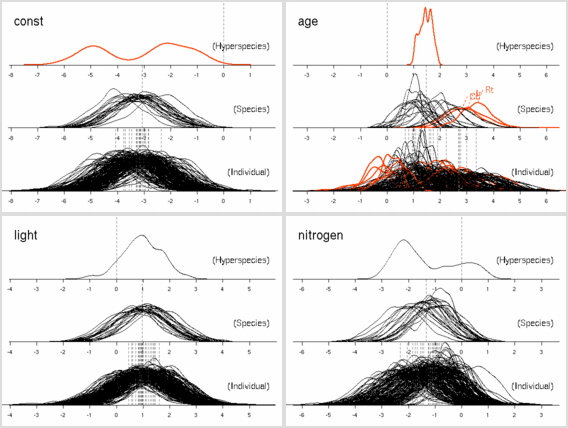
  ここで問題なのは， hyperspecies - species - tree の層において， hyperspecies - species までならば明らかに 「窒素が多ければ死亡確率は低下」に見えた現象が， 個体内での補正 (上の図) とでも言うべきパラメーター推定によって， 「窒素と死亡確率は無関係」 となったことだ．

  とか書いてるけど， じつは
  • 種間では「窒素多いと長命化」
  • 種内では「窒素多いと短命化に見える」 (実際には「明るさ」との交絡)
  となってるような結果が得られつつあるような気がする．
• 真夜中すぎ， 10 MCMC step とばしの粗い計算結果 (まだ収束も十分ではない) が得られた． あとで自分で見てわからなくなるので補足しておくと，
  • 線形部品の age と light は exp() 内の量である
  • nitrogen は hyperspecies の層だけにパラメーターがある
  で， パラメーターの事後分布だけみると， たしかに窒素量が (初期) 死亡確率を引き下げてる， ってのがはっきりしてるみたいなんだけど ……

• しかしながら， 全個体に関して葉の平均寿命を計算して， その樹種ごとの平均窒素量とやらと比較しても いまいち明確ではない． ふーむ?

[推定平均寿命 vs 窒素]

窒素はほとんど無関係， に見えるが …… 横軸の重量あたり窒素量の種内平均値は平均寿命を伸ばすはず， なんだけど? まあ， 窒素は葉齢の効果にかかる項ではないんで， 単に 「死亡確率が高くなる時期は遅くなる」 (その後の死亡確率上昇は高い) ということなのかもしれないけれど．

• なんかまた交絡してるのか． あるいは死亡確率の関数型の問題か? よくわからぬまま撤退． 50 MCMC step とばしの計算を命じておく． 2550 研究室発． 2605 帰宅．
• [今日の運動]
  • ひたすらうんどう不足
• [今日の食卓]
  • 朝 (0830): 食パン．
  • 昼 (1500): 研究室お茶部屋． 北大生協サンドイッチ．
  • 晩 (2230): Sunkus サラダ巻． 295 円．