更新: 2015-02-04 14:20:41
生態学のデータ解析 - 例/car.normal()
ここでは 2008 年生態学会大会 (福岡) の ベイズ企画集会 の 久保コメント (PDF file, 0.06 MB) で使った「もっとも簡単な空間相関 (空間的自己相関) あり統計モデル」(一次元の CAR model) を WinBUGS で計算する方法を説明します.
- 統計モデリング入門 の第 11 章にも解説あります
- 解説記事 「簡単な例題で理解する空間統計モデル」
- 原稿ファイル (PDF ファイル, 北大図書館 HUSCAP)
- 久保拓弥. 2009. 簡単な例題で理解する空間統計モデル (特集: 始めよう! ベイズ推定によるデータ解析). 日本生態学会誌 59:187-196
- 同じ特集号の他の解説記事: http://tombo.sub.jp/bayes.html
- 参照: R のインストール, WinBUGS のインストール, car.normal() 雑, R2WinBUGS, 空間統計学, ベイズ統計 & MCMC
-
car.normal()のパラメーター設定については car.normal() 雑 を参照
-
- WinBUGS の
car.normal()とは intrinsic Gaussian CAR model にもとづいてガウス確率場 (Gaussian random field) を生成する関数です- 参照: GeoBUGS User Manual
- 2007 年統計学授業 (第 7 回) にも同じように実行可能な例題ファイル (簡単な階層ベイズモデル) をおいています
[もくじ]
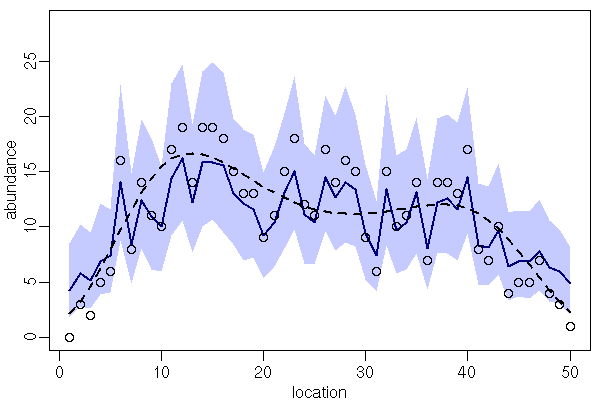
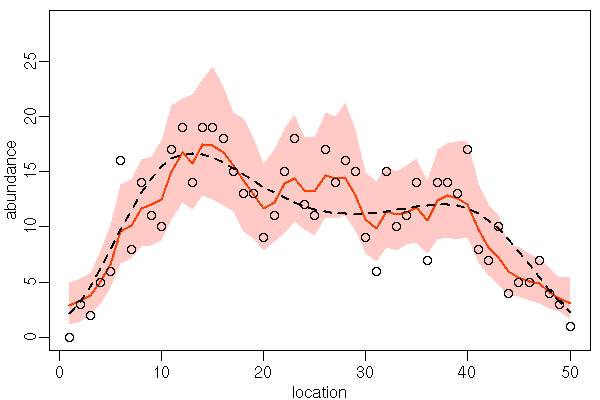
ここであつかう例題とは?
- ポアソン乱数関数を使って生成した架空データを使っています
- 50 個の観測地点が一次元空間上に等間隔にならんだ調査地
- 観測地点名 (locaiton) は「左」から 1, 2, 3, ..., 50
- 各観測地点で生物の個体数 (abundance)
Yを観測した- 破線は「各地点のホントの平均 abundance」
m(人間には観測できない)
- 破線は「各地点のホントの平均 abundance」
- 人間が観測するかぎり第 1 - 50 地点の環境はすべて同じ (均質な環境) に見える
- 問題: 観測地点間の空間相関 (空間的自己相関) を考慮して生物の密度を推定せよ
car.normal() の使用例
- 観測場所間の空間相関を考慮したベイズモデル (階層ベイズモデルの一種) を WinBUGS と R で推定計算する方法を説明します.
- とりあえずここでは空間相関を考慮したベイズモデルのしくみについての説明は省略して,「どうやって推定計算してみせたのか」だけを説明します.
R2WinBUGS を使った計算の手順と準備
全体の手順はこうなります:
- R で観測データ (ここでは架空データ) の準備,空間構造の定義,パラメーターの初期値などを設定
- R が WinBUGS を呼びだしてベイズモデルのパラメーター推定のための MCMC 計算させる
- WinBUGS の推定計算結果を R がうけとる
- R 内で収束診断やさまざまな作図など
このために必要な準備は以下のとおりです:
- R のインストール
- R の
library(R2WinBUGS)のインストール- R 内で
install.pacakges("R2WinBUGS",dependencies=TRUE)
- R 内で
- WinBUGS のインストール
必要なファイル
- Y.RData: 上の図で示されてるような架空データを格納している RData file,これを
load("Y.RData")することで以下のオブジェクトが R に読みこまれる:-
Y: 上の図で点々で示されている架空観測値 -
m: 上の図で破線で示されている各地点における「本当の」平均値
-
- model1.bug.txt: BUGS 言語で定義されたベイズ空間統計モデル
# model1.bug.txt は空間相関を考慮したベイズモデルを定義している
model
{
Tau.noninformative <- 1.0E-2 # 無情報事前分布 (正規分布) の分散逆数
P.gamma <- 1.0E-2 # 無情報事前分布の (ガンマ分布) の分散逆数
for (i in 1:N.site) {
Y[i] ~ dpois(mean[i]) # 観測データと密度の関係
log(mean[i]) <- beta + re[i] # 密度は (全体の平均) x (場所差)
}
re[1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau) # 場所差を CAR model で生成
beta ~ dnorm(0, Tau.noninformative) # 全体の平均は無情報事前分布にしたがう
tau ~ dgamma(P.gamma, P.gamma) # 場所差のばらつきは無情報事前分布にしたがう
}
-
上の BUGS コードについての補足注意:
betaの事前分布はこれでよいのか? - この問題について berobero さん からご指摘をいただきました (2013-09-03)
-
「切片」
betaの事前分布はdflat()(improper な無情報事前分布) がよいでしょう (上のようにdnorm()な無情報事前分布を使うよりも) - 理由: GeoBUGS User Manual にそう書いてあるから
-
runbugs1.R (注: runbugs1.R ではなく runbugs.R を使用してください)
: 上の
model1.bugs.txtを WinBUGS 上で実行させるための R スクリプト- 推定計算用のデータのセット (car.normal() 雑 参照)
- パラメーター初期値
- WinBUGS が実施した推定計算結果のうけとり
# runbugs1.R は下のようにデータの準備,パラメーターの初期化など
# そして WinBUGS の呼び出しとその結果のうけとりを実行する
source("R2WBwrapper.R") # R2WBwrapper.R の読みこみ
clear.data.param() # for initialization
# set data (WinBUGS にわたすデータの準備)
load("Y.RData")
set.data("N.site", length(Y))
set.data("Y", Y)
Adj <- c(sapply(2:(N.site - 1), function(a) c(a - 1, a + 1)))
set.data("Adj", c(2, Adj, N.site - 1)) # 「近傍」ID の定義
set.data("Weights", rep(1, 2 * N.site - 2)) # 近傍の重み (全部 1)
set.data("Num", c(1, rep(2, N.site - 2), 1)) # 近傍の個数 (1, 2, 2, ... , 2, 1)
# set parameter (WinBUGS にわたすパラメーター初期値などの準備)
set.param("beta", 0)
set.param("re", rnorm(N.site, 0, 0.1))
set.param("tau", 1)
post.bugs1 <- call.bugs( # ここまで準備したデータとパラメーターをわたして
file.bug = "model1.bug.txt", # model1.bug.txt で定義されているベイズモデルを
n.iter = 200, n.burnin = 100, n.thin = 1 # このような MCMC step で
) # 推定計算して結果を post.bugs1 に格納しろ,という命令
-
R2WBwrapper.R:
runbugs1.Rで使う RtoWinBUGS のラッパー関数定義ファイルlibrary(R2WinBUGS)は何とも使いづらいのでこういう「R2WinBUGS をラップする関数群」を定義した
R2WinBUGS で推定計算
- 上のように準備ができれば,あとは
runbugs1.Rを R で実行させるだけです- たとえば下のように R のコマンドラインで
source("runbugs1.R")と指示すると,runbugs1.Rの読み込み,その内容を実行します
- たとえば下のように R のコマンドラインで
- WinBUGS が計算を終えると何やら奇妙なグラフをだして停止するので,WinBUGS を「終了」します
- すると WinBUGS の推定計算結果が R 内の
post.bugs1に格納されます
WinBUGS で得られた推定結果を R で調べる
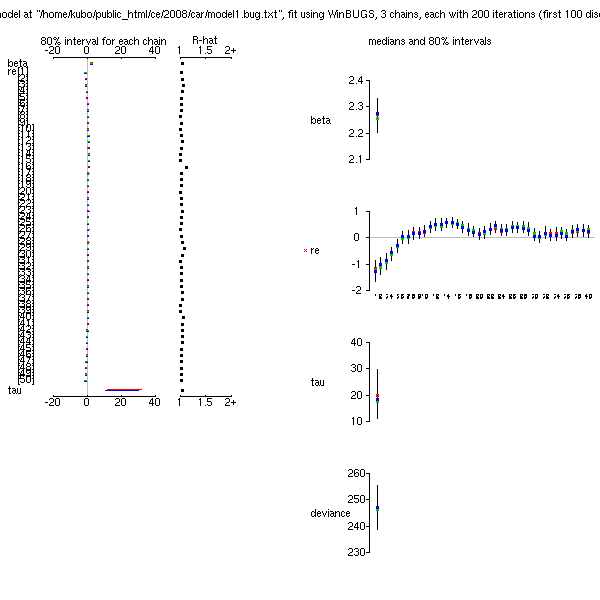
-
plot(post.bugs1)とすると,下のような図が得られます- 左側は収束のよさを R-hat 値であらわし,右は事後分布の中央値と 80% 区間が示されています
-
print(post.bugs1,digits.summary=3)とすると mcmc1.txt にあるような事後分布表が出力されます
R を使って事後分布の作図
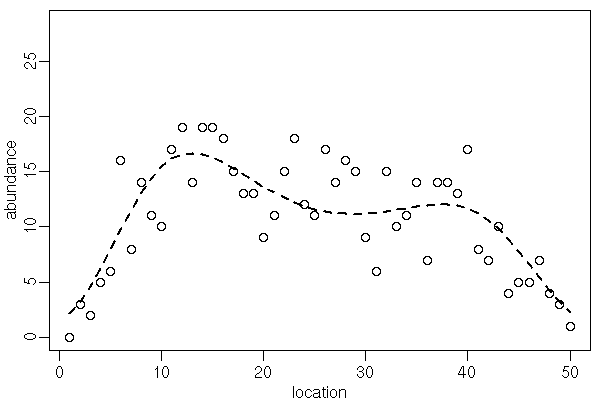
- plotcar.R を
source("plotcar.R")してからplotcar(post.bugs1)とすると,下のような図が出力されます
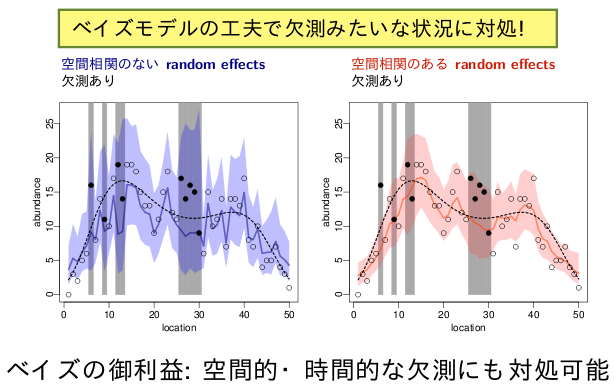
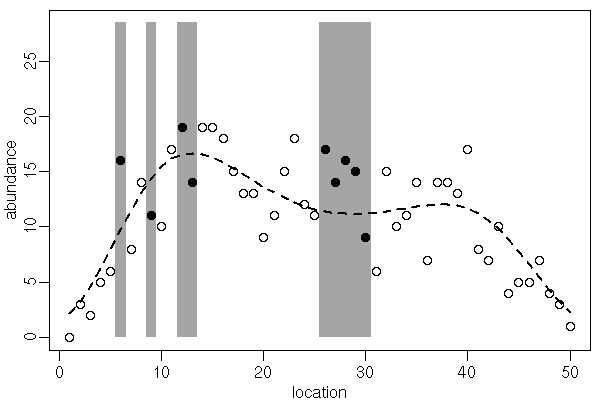
補足 1: 観測データに欠測がある場合
- 下の図のように欠測 (黒丸) がある場合の推定計算方法について説明します
- 黒丸は欠測つまり観測されなかった観測値です
- じつはこれは (BUGS 言語で書かれた) 統計モデルを変更する必要はありません
- 観測データ (ここでは
Y) に欠側値NAをまぜてやるだけで OK です- WinBUGS user manual 参照してください
- 観測データ (ここでは
必要なファイル
- Y.RData: 上の例と同じ
- model1.bug.txt: 上の例と同じ (変更の必要なし!)
-
runbugs2.R: 上の例の
runbugs1.Rをちょっとだけ変更したもの
# (runbugs1.R と runbugs2.R の相違)
# set data
load("Y.RData")
v.na <- c(6, 9, 12, 13, 26:30) # 欠測の生じた場所
YwithNA <- Y
YwithNA[v.na] <- NA # つまりデータ vector に NA があると
# WinBUGS はその地点を欠測とみなす
set.data("N.site", length(YwithNA))
set.data("Y", YwithNA)
(途中おなじ,中略)
post.bugs2 <- call.bugs( # post.bugs2 に結果を受け取らせている
file.bug = "model1.bug.txt", # BUGS コードは上の例と同じ,変更の必要なし
n.iter = 200, n.burnin = 100, n.thin = 1
)
> # つまりデータがこう変わるということです > # (欠測なしの Y) > Y [1] 0 3 2 5 6 16 8 14 11 10 17 19 14 19 19 18 15 13 13 9 11 15 18 12 11 [26] 17 14 16 15 9 6 15 10 11 14 7 14 14 13 17 8 7 10 4 5 5 7 4 3 1 > # (欠測ありの Y) > Y [1] 0 3 2 5 6 NA 8 14 NA 10 17 NA NA 19 19 18 15 13 13 9 11 15 18 12 11 [26] NA NA NA NA NA 6 15 10 11 14 7 14 14 13 17 8 7 10 4 5 5 7 4 3 1
- R2WBwrapper.R: 上の例と同じ
R2WinBUGS で推定計算,結果の作図
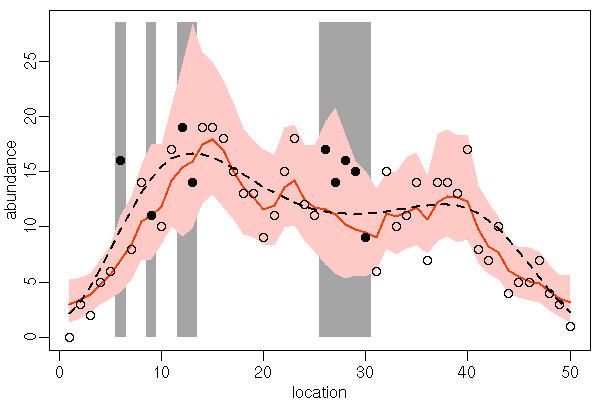
- 上のように準備ができれば,あとは
runbugs2.Rを R で実行させるだけです - 今回は推定計算の結果が R 内の
post.bugs2に格納されます - plotcar.R を
source("plotcar.R")- 注意: この
plotcar.Rは 2008-03-25 に改訂 (欠測値表示をできるようにした) したものです (古い version のものをもっている人はいれかえてください) - 次に
plotcar(post.bugs2,v.na=v.na)とすると,下のような図が出力されます-
v.naはrunbugs2.Rの中で定義されている「欠測のあった位置」です
-
- 注意: この
補足 2: 各地点独立とした場合
- ついでながら,空間相関なし random effects,つまりごくふつーの階層ベイズモデルで「場所差 random effects」(各地点完全独立を仮定している) を表現する場合はどう計算するのかを説明します
必要なファイル
- Y.RData: 上の例と同じ
- model3.bug.txt: 空間相関なし版モデル
- 蛇足: 下の BUGS code はわかりやすさを重視した書きかたで,じつはもっと計算速度が速く収束もよい書きかたがあります (参照: ぎょーむ日誌 2008-09-08) -- ただしこれは
dnorm()などでしか使えません (car.normal()では使えない)
- 蛇足: 下の BUGS code はわかりやすさを重視した書きかたで,じつはもっと計算速度が速く収束もよい書きかたがあります (参照: ぎょーむ日誌 2008-09-08) -- ただしこれは
model
{
Tau.noninformative <- 1.0E-2
P.gamma <- 1.0E-2
for (i in 1:N.site) {
Y[i] ~ dpois(mean[i])
log(mean[i]) <- beta + re[i]
re[i] ~ dnorm(0.0, tau) # 各地点独立な random effects
}
beta ~ dnorm(0, Tau.noninformative)
tau ~ dgamma(P.gamma, P.gamma)
}
-
runbugs3.R: 上の例の
runbugs1.Rをちょっとだけ変更したもの
source("R2WBwrapper.R")
clear.data.param() # for initialization
# set data
load("Y.RData")
set.data("N.site", length(Y))
set.data("Y", Y)
# Adj, Weights, Num の設定は不用
# set parameter
set.param("beta", 0)
set.param("re", rnorm(N.site, 0, 0.1))
set.param("tau", 1)
post.bugs3 <- call.bugs( # post.bugs3 に結果を受け取らせている
file.bug = "model3.bug.txt",
n.iter = 200, n.burnin = 100, n.thin = 1
)
- R2WBwrapper.R: 上の例と同じ
R2WinBUGS で推定計算,結果の作図
- 上のように準備ができれば,あとは
runbugs3.Rを R で実行させるだけです - 今回は推定計算の結果が R 内の
post.bugs3に格納されます - plotcar.R を
source("plotcar.R")
> # (R 内で) > plotcar(post.bugs3, col1 = "#0000ff", col2 = "#ccccff")