pkgconfig
をインストールしてなかった,
なる Vine Linux に固有な問題であるように思われるので,
本日はただ単に
(pkgconfig がすでにインストールされた状況で)
time rpm -ba --clean ./R.spec
すればよい,
と.
また 83 分かかってコンパイル
……
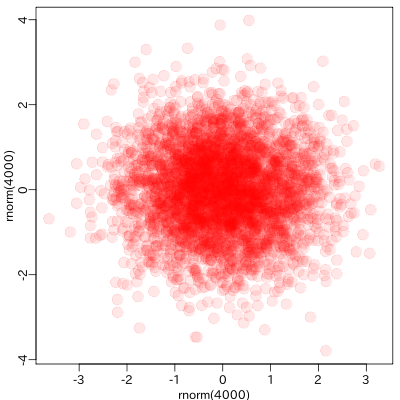
cairo R ができた!
X11()
や
png()
といった device で下のような半透過 (semi-transparent)
な作図ができる.

$HOME/.Rprofile
にて grDevices::X11.options(type = "cairo")
その他あれこれと設定すればよい,
と.
しかし,
Ripley 教授系の library(grDevices)
な cairo device と,
Simon 系の library(Cairo)
が並立する現状,
将来はどうなっていくんでしょうねえ
……
(後記:
cairo な X11()
はみょーに描画速度が遅い場合がある,
とわかった.
grDevices::X11.options(type = "Xlib")
にしておいて,
必要なときだけ type = "cairo"
にしたほうがよいかも)
/usr/local/psa/var/log/maillog.processed
の記録をみると,
May 19 00:37:10 ve441 qmail: 1242661030.636380 delivery 43482:
deferral:
Connected_to_157.80.12.22_but_sender_was_rejected./
Remote_host_said:_450_4.7.1_Access_denied._IP_name_lookup_failed_
[203.104.99.221]/
……
えーい,
つまり茨城大のメイルサーヴァーが
「203.104.99.221 (これは生態学会さーばー)
とかいう DNS 逆引きができないところからきたメイルなんて受けとれるか!
どうせスパムだろ!」
と決めつけてくれている,
とわかった
……
たしかに生態学会さーばーから送られてくるようなメイルってのは,
もっぱら研究を妨害するスパムである確率が高いのはたしかなのだが
……
IPアドレスの所有者は、業務提携先のライブドア社となっておりますので、 現在逆引きが可能か確認をしております。なんと livedoor の DNS server 使ってたのか. 夕方には逆引きできるようになった.
「ちょっと待って下さい.いま観測結果が出てきました.あの艦は,やっぱり進行方向と 直角に加速しています.我々のレーダー観測時には,太陽と本艦を結ぶ線上に あの艦は入っていました.方向角の誤差は数秒くらいなもんです」
「本当か? 偶然じゃないだろうな」
「間違いありません.どんぴしゃりでそこにおさまっています」
「ということは,掩蔽の観測をしやがったのか.ただ者じゃないな…….奴らは」
(中略)
敵は掩蔽を利用して哨戒艦の観測を行った. 光学観測は,普通なら他のセンサの補助手段としてしか使用されない. 目標が太陽を背後にしている時は, 特にそうだ. しかし, 掩蔽が起こるときは事情が異なる. 精度のいい光学望遠鏡があれば, 太陽の光球面をよぎる艦影をとらえて,速度や移動方向を知ることができる.
X11(type = "cairo")
は
X11(type = "Xlib")
に比べてかなり描画速度が遅いような気がする.
$HOME/.Rprofile
は
grDevices::X11.options(type = "Xlib")
と設定しておいて
(cairo が使えれば type
は自動的にそちらを使ってしまう),
必要なときだけ cairo したほうがよいかも.
library(Cairo)
の
CairoX11()
は多少速い (?)
ような気がする.
<updated>2009-05-24T16:26:40+09:00</updated>
タグを改善する,
といった案件で
……
自分で構築したシステム
(ヒトことで言えば,テキストベイスのデータベイス)
なんだけど,
このあたり不必要に複雑ぎみなので
改良作業にも時間がかかる.
car.normal()
な GRF もまた MRF の一種である).
P.err = 0.001
などと決めてやらねばならない
……
P.err にほぼ支配されている),
あんまし確率場 (random field) ってかんぢではなくなる
……
dbern(p[i]))
からばいのみある
(dbbin(p[i], N.size))
に拡張してみる
……
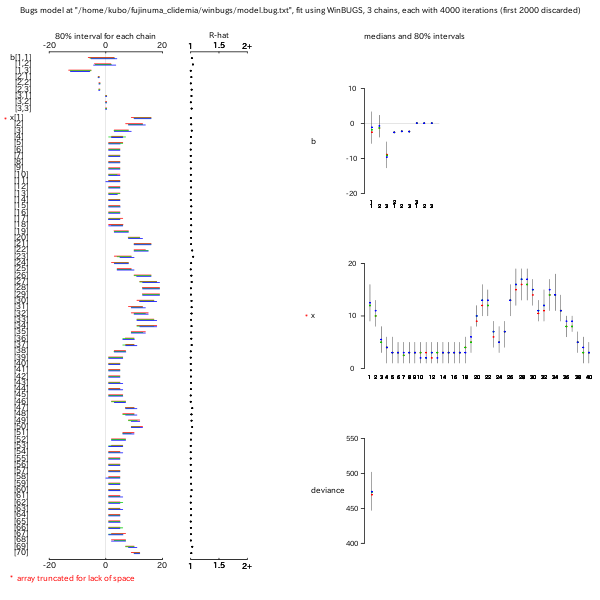
Distance
依存性がない最単純モデルによる推定
(BUGS code).
この程度の計算は,
さすがに収束する.
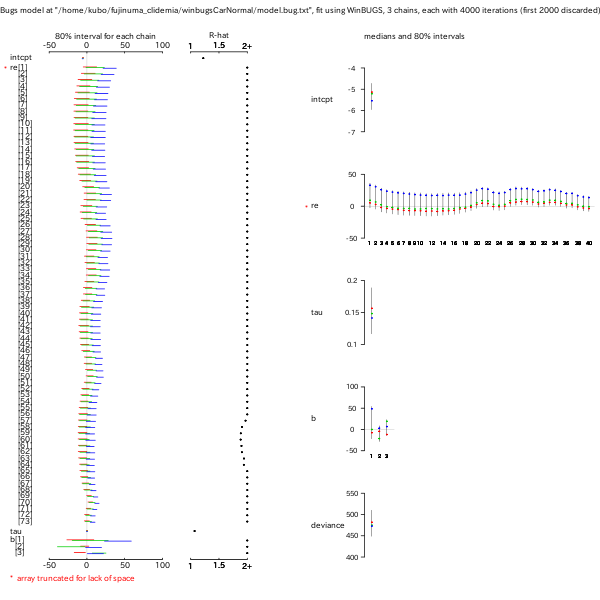
intcpt なる「切片」パラメーターの有無にある.
GRF なほうでは intcpt
ナシではうまく収束せず,
binomial MRF なやつだとこういう「切片」パラメーターは
ただのジャマもの (ということに北大構内走の最中に気づいた).
intrinsic Gaussian CAR normal なモデルは計算はカンタンなんだけど
(条件つき局所確率は単純な正規分布にしたがうから),
その「実態」の理解は私などにはなかなか難しい
(確率場全体を簡単な多変量確率分布で定義するのが難しそう)
といったシロモノなのだが
……
もしこの
car.normal()
で生成される GRF をひとつの多変量正規分布 (?) で書けるとすると,
その「各地点の平均はことごとくゼロ」
と設定されているはずだ,
とわかった
(ただし分散共分散行列のほうはナゾで,
定義できないのではないかと思う
……
まあこのあたり variogram と対応可能な GRF
あたりから勉強しなおすべきかも).
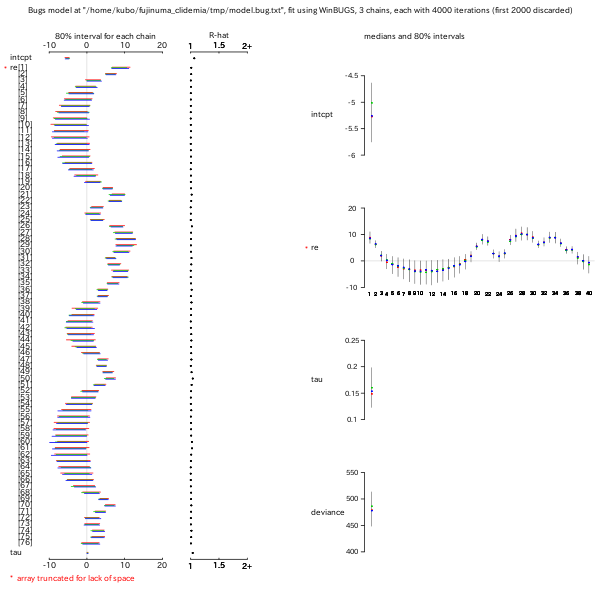
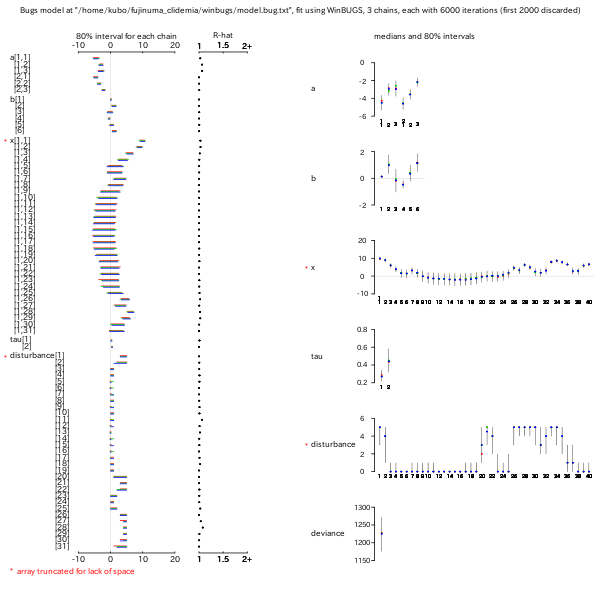
Distance 依存性も推定させようとしたもの
(BUGS code,
事後分布表).
上の binomial なやつではまがりなりにも距離依存性を
推定できていたわけだが,
こちらの GRF なやつだとかくのごとくコケてしまいます,
と.
glm()
によるやや複雑なモデリング
……
「あろめとりっく」なハナシなので,
説明変数を log.x
としながら,
family = gaussian(link = "log")
とするわざ
(今年 3 月の盛岡での GLM 自由集会
の久保投影資料を参照).
car.normal()
では説明変数的なパラメーター数の個数を減らしてもダメ,
とわかった.
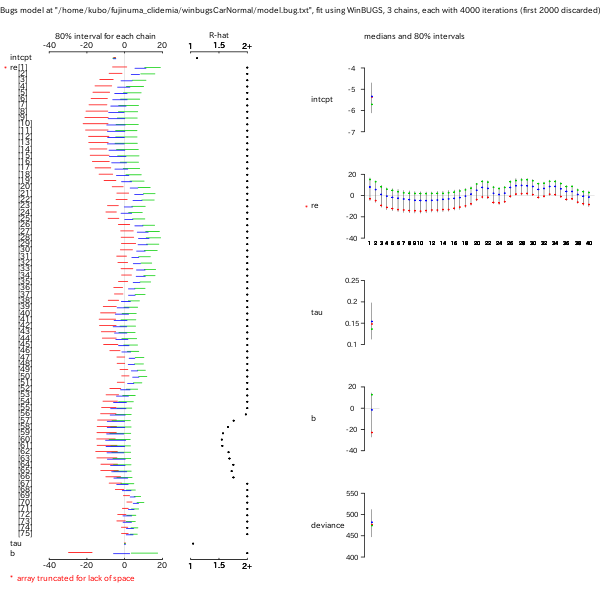
dbin()
の size を増やすと (みかけのうえで)
ばらつきは減る.
ただし計算には時間がかかる (二項乱数の生成を考えるとそうかも).
1200 秒ぐらい.
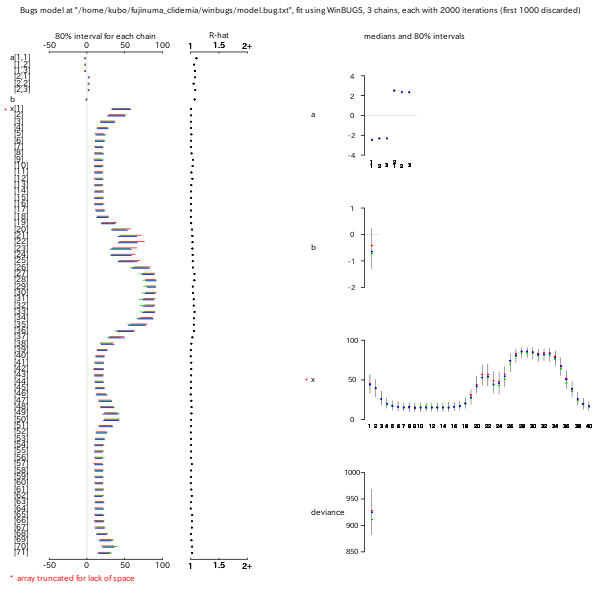
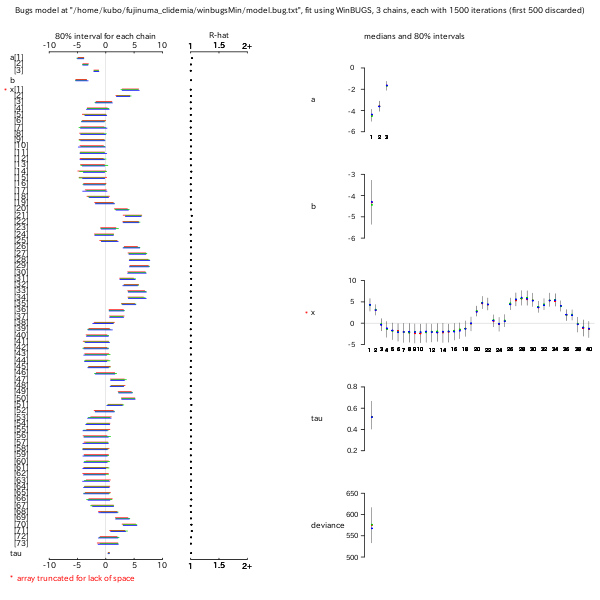
car.normal()
関数にたよるのではなく,
BUGS code
内で自分で書いてしまう,
ということ.
それによって小細工を混入させうる余地が生じる.
小細工のカギは局所的な条件つき確率の定義にあり,
x[i] ~ dnorm(q[i], tau) q[i] <- (x[LeftRight[i, 1]] + x[LeftRight[i, 2]]) * 0.45の 2 行目で 0.5 ではなく 0.45 にしている, というところ. 0.5 にすると
car.normal()
と同じ動作になってしまう (そして収束しない).
x[i] ~ dnorm(q[i], tau) q[i] <- (x[LeftRight[i, 1]] + x[LeftRight[i, 2]]) * wとしたときに
w が 0.5 より小さい正の値であれば
(そんなにいろいろ調べたわけではないが),
まあだいたい同じような結果に収束する
w = 0.49
など 0.5 に近づけていくと,
徐々に収束が遅くなる
w = 0.5
は「臨界点」みたいな値で,
この値だと一気に収束が遅くなる
(あるいは永久に収束しない?)
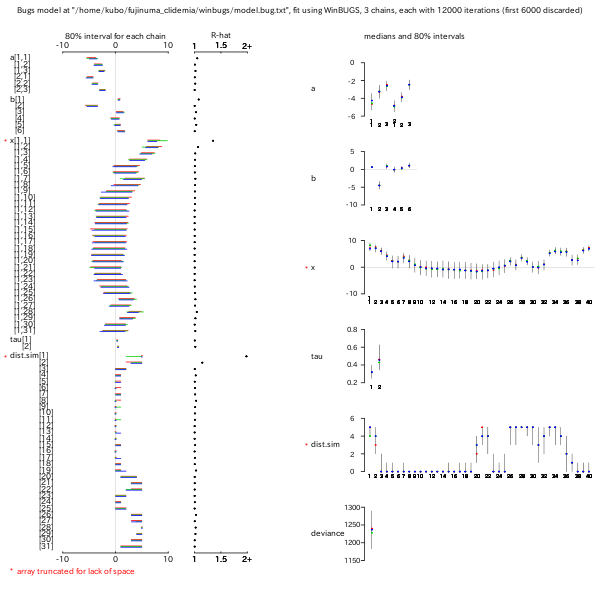
Nobs[i] ~ dbin(p[i], N.size) logit(p[i]) <- a + xN[i] Mobs[i] ~ dpois(q[i], N.size) log(q[i]) <- b0 + b1 * xN[i] + xM[i]といった BUGS コードで,
i: 場所
Nobs[i], Mobs[i]: 観測値
xN[i], xM[i]: 潜在変数 (状態変数)
log(q[i]) <- b0 + b1 * xN[i] + xM[i]といったかんじで, 「状態変数
xN[i] をそのまま
状態変数 xM[i] の説明変数に使う」
というのはマズい場合があるかもしれない.
xN[i] が xM[i] のあてはめに
「ふりまわされる」
ような状況になることがある.
Nobs[i] ~ dbin(p[i], N.size) n.simulated[i] ~ dbin(p[i], N.size) logit(p[i]) <- a + xN[i] Mobs[i] ~ dpois(q[i], N.size) log(q[i]) <- b0 + b1 * n.simulated[i] + xM[i]このように
n.simulated[i]
なる補助的な状態変数
(N なる量を ``simulate'' した量)
を説明変数にすると,
xN[i] が xM[i]
にあまり影響されなくなる.
影響されないほうが良い場合には,
このように定式化したほうがよい.
(そして n.simulated[i]
も「それっぽい」値を引いて「なんちゃって中央化」
をすると収束が改善される).
(x_left + x_right) * 0.5
で評価すると収束がむちゃくちゃに遅くなる
(もしくは永久に収束しない?)
(x_left + x_right) * 0.45
といったナゾのやり口だと問題なく収束しているように見える
link = identity),
さらに「近傍」にも必ず影響される
(このあたりが pseudo likelihood 的)
glmmML()
の最尤推定は収束しない
(sigma が無限に小さくなるから).
glmmML 紹介
にも追記.