n.sample
はふぞろい,
という状況
(前回は n.sample = 5 と固定).
> (data <- data.frame(id = 1:4, n.sample = c(4, 3, 5, 5),
x = c(2, 1, 3, 4), y = c("red", "yellow", "green", "blue")))
id n.sample x y
1 1 4 2 red
2 2 3 1 yellow
3 3 5 3 green
4 4 5 4 blue
まず,
こいつを n.sample の回数ぶんだけ
タテにのばす.
この「のばし」わざ!
> (Data <- data[rep(1:nrow(data), data$n.sample),])
id n.sample x y
1 1 4 2 red
1.1 1 4 2 red
1.2 1 4 2 red
1.3 1 4 2 red
2 2 3 1 yellow
2.1 2 3 1 yellow
2.2 2 3 1 yellow
3 3 5 3 green
3.1 3 5 3 green
3.2 3 5 3 green
3.3 3 5 3 green
3.4 3 5 3 green
4 4 5 4 blue
4.1 4 5 4 blue
4.2 4 5 4 blue
4.3 4 5 4 blue
4.4 4 5 4 blue
つぎに x 列を {0, 1} におきかえる.
mapply()
を使う.
mapply()
の使いどころとはこういうところだったのか
……
> Data$x <- ifelse(unlist(mapply(seq, data$x, 1+data$x -data$n.sample)) > 0, 1, 0)
> Data
id n.sample x y
1 1 4 1 red
1.1 1 4 1 red
1.2 1 4 0 red
1.3 1 4 0 red
2 2 3 1 yellow
2.1 2 3 0 yellow
2.2 2 3 0 yellow
3 3 5 1 green
3.1 3 5 1 green
3.2 3 5 1 green
3.3 3 5 0 green
3.4 3 5 0 green
4 4 5 1 blue
4.1 4 5 1 blue
4.2 4 5 1 blue
4.3 4 5 1 blue
4.4 4 5 0 blue
さて,
ここでなぜこのように「手品」のごとく {0, 1}
変換ができるのか説明してみよう.
まず
mapply()
部分だけを動かしてみると
> mapply(seq, data$x, 1+data$x -data$n.sample) [[1]] [1] 2 1 0 -1 [[2]] [1] 1 0 -1 [[3]] [1] 3 2 1 0 -1 [[4]] [1] 4 3 2 1 0このような整数 vector の list になっていることがわかる.
unlist()
すると
> unlist(mapply(seq, data$x, 1+data$x -data$n.sample)) [1] 2 1 0 -1 1 0 -1 3 2 1 0 -1 4 3 2 1 0全部くっついた vector になり, さらに不等式にわたすと
> unlist(mapply(seq, data$x, 1+data$x -data$n.sample)) > 0 [1] TRUE TRUE FALSE FALSE TRUE FALSE FALSE TRUE TRUE TRUE FALSE FALSE TRUE TRUE [15] TRUE TRUE FALSElogical 型 (
{TRUE, FALSE})
vector になるので ifelse(..., 1, 0)
すれば {0, 1} 変換できる.
> dimnames(Data)[[1]] <- 1:nrow(Data) # rownames(Data) <- 1:nrow(Data) でも可 > Data id n.sample x y 1 1 4 1 red 2 1 4 1 red 3 1 4 0 red 4 1 4 0 red 5 2 3 1 yellow 6 2 3 0 yellow 7 2 3 0 yellow 8 3 5 1 green 9 3 5 1 green 10 3 5 1 green 11 3 5 0 green 12 3 5 0 green 13 4 5 1 blue 14 4 5 1 blue 15 4 5 1 blue 16 4 5 1 blue 17 4 5 0 blueいやー, すばらしいですね ……
library(lme4)
まわりでいろいろと試行錯誤してみる.

いつもの感想なんですけど,これを読むたびにここであつかってる 気象条件→直径成長問題の難しさを感じます (が,まだ現状では誰もうまいモデリングはできていないでしょう). そしてこの原稿をまとめておられるときの鍋島さんの苦労 (?) が感じられるような気がします. 難しい現状がよくまとめられているとも思います.
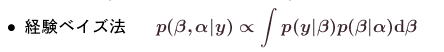

library(lme4) fit <- lmer( dormancy ~ (1 | spc) + (1 | id) + light + (0 + light | spc), family = binomial, data = d, method = "Laplace" )推定結果はこんなかんぢで.
Generalized linear mixed model fit using Laplace
Formula: dormancy ~ (1 | spc) + (1 | id) + light + (0 + light | spc)
Data: d
Family: binomial(logit link)
AIC BIC logLik deviance
532 553 -261 522
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 2.66e-01 5.16e-01
spc light 5.00e-10 2.24e-05
spc (Intercept) 1.99e+00 1.41e+00
number of obs: 562, groups: id, 105; spc, 22; spc, 22
Estimated scale (compare to 1 ) 0.8859
Fixed effects:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.636 0.354 -1.80 0.072
light -1.668 0.301 -5.55 2.9e-08
Correlation of Fixed Effects:
(Intr)
light -0.317
library(lme4)
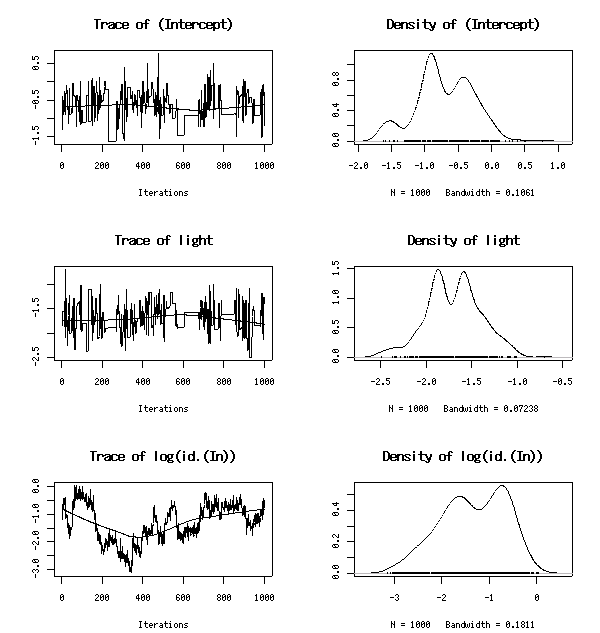
mcmcsamp()
を使って事後分布のサンプリング
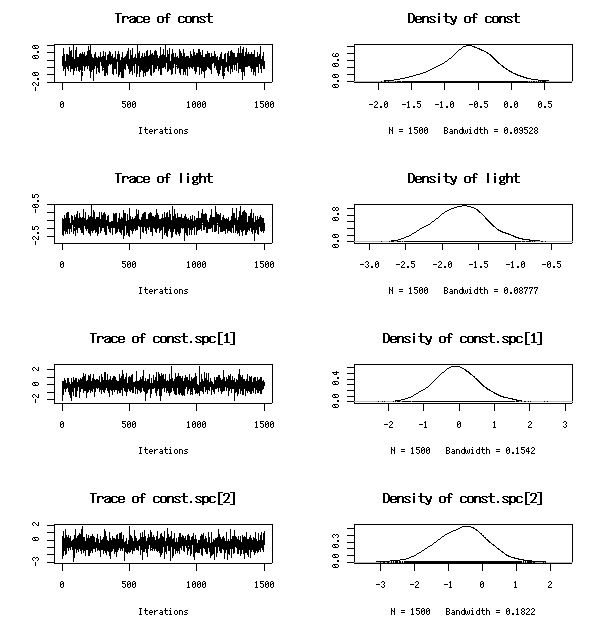
m <- mcmcsamp(fit, n = 1000) library(coda) plot(m)を試みてみると …… 意外にもというか, この mcmcsamp() の MCMC 計算 (おそらくこの挙動からみて Metropolis-Hastings 法) はへぼい場合がある, ということがわかった.
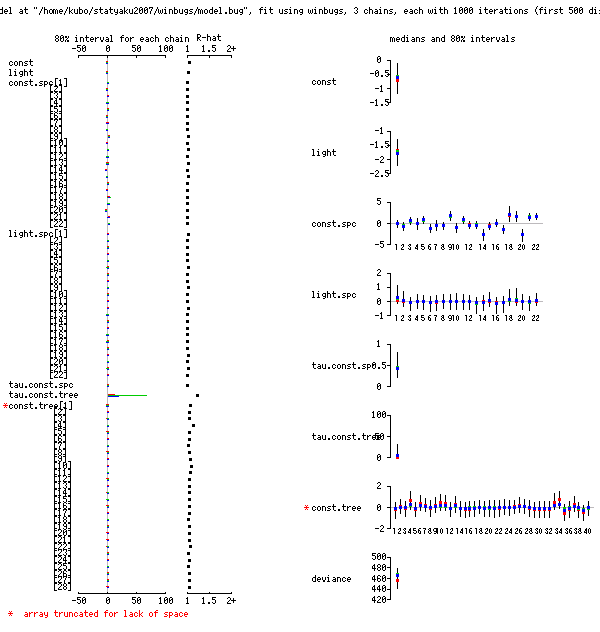
多重比較や多重検定のときに有意確率の補正がなぜ必要になるのか、補正するならどういう状況ではどのように補正すべきなのかといったことには関係なく、” 複数の似たような検定ができるなら多重検定の補正をするものだ”という思い込みの方に重きを置く人はけっこう多いということであろう。葬式のときに黒いネクタイをしていかずにいろいろ言われた人(あるいは言われているの見聞きした人)がどこでも黒いネクタイで大威張りみたいなものだろうと思うのだが。ホントに, この回に登場する 「ブロックごとに検定 → 多重検定」 なヒトたち, 何のために苦労してわざわざぶろっくなんかを …… かーごかると 統計学とでも命名してみようか?
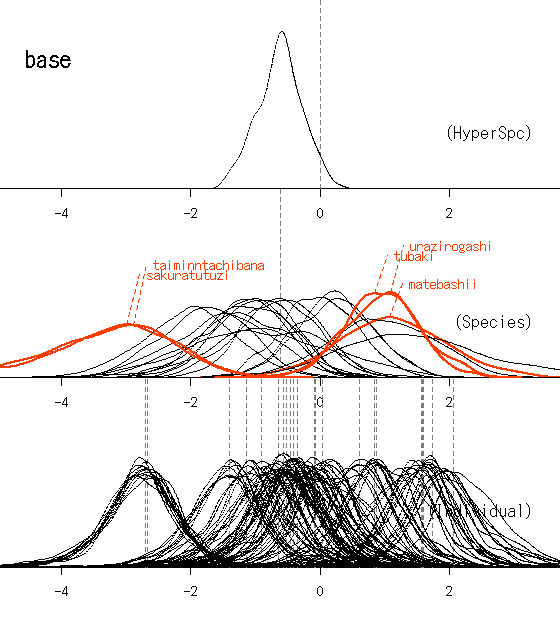
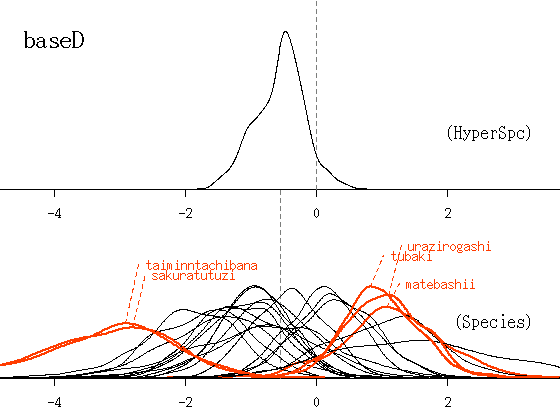
library(grid)
graphics なぷろぐらみんぐ
……
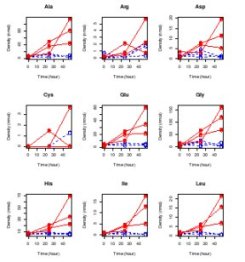
22 樹種のシュート伸長休眠 (D) と二度伸び (L),
その明るさ依存性,
と.
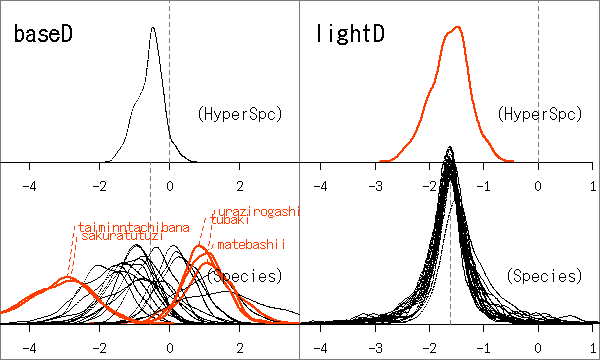
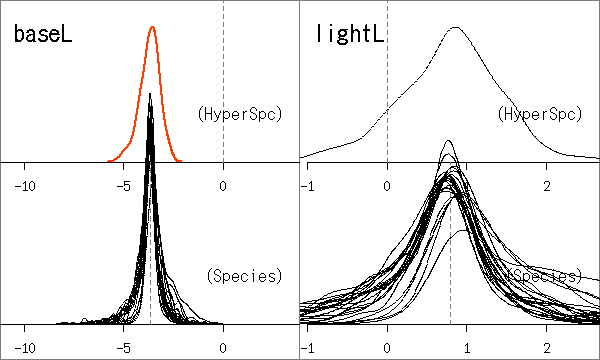
viewport)
の中に図をとじこめる方法」
がわかった
(cf.
help(viewport)).
pushViewport(viewport(..., clip = "on"))
と指示すればよい
上の図では左右ははみだしてないけど,
上下には貫通してもよいようにしている.
pushViewport(viewport( x = 0.5, y = 0.5, h = 1, w = 1, layout = grid.layout(1, 2) )) pushViewport(viewport( layout.pos.row = 1, layout.pos.col = 1, clip = "on" # ここが重要! )) # ... 左側作図関数よびだし ... popViewport() pushViewport(viewport( layout.pos.row = 1, layout.pos.col = 2, clip = "on" # ここが重要! )) # ... 右側作図関数よびだし ... popViewport() popViewport()
library(grid) 作表プログラミング,
牛原さんのシュート伸長に関する
562 シュート
/ 105 個体
/ 22 樹種
全データ視覚化.
休眠 (D), 通常 (N), 二度伸び (L) シュートを樹種ごと &
個体ごとに.
樹種ごとの標本個体数,
そして樹木個体ごとの標本シュート数が異なるので下のようになる.
樹種によっては明暗両環境がそろっていない.
参考のため休眠パラメーター図も再掲しとこう.


library(grid)
の使いかたの勉強にはなったが
……
(来週の授業にしろ 3 月の生態学会ポスター発表にしろ)
LaTeX でモノを作るわけだから,
こんなふうに「図な表」にしちまうとまずかったかしらん?
ネット上に掲載するには
png()
出力が便利なわけだが
……
png()
ではなく
postscript(..., paper = "special")
で EPS ファイルと出力すればいいや.
この「図な表」ならそんなにかさばらないし
……
それに対して nested 事後分布図なんかは EPS にすると
ちょー巨大ファイルになるだろうから PNG 出力せざるをえない.

> toupper("abc")
[1] "ABC"
> tolower("ABC")
[1] "abc"
> chartr("AB", "ab", "ABC") # AB だけを置換
[1] "abC"
それでは「最初の一文字だけ置換」
やりたければどうすればよいか?
たとえば最初の一文字だけがヘンな場合は簡単で
> tolower("Abc")
[1] "abc"
となる.
それでは abc を Abc
としたい場合には?
これは残念ながら単純ではないらしく,
さきほどの
toupper(), tolower() のhelp()
の Examples
にあるような関数
capwords <- function(s, strict = FALSE) {
cap <- function(s) paste(toupper(substring(s,1,1)),
{s <- substring(s,2); if(strict) tolower(s) else s},
sep = "", collapse = " " )
sapply(strsplit(s, split = " "), cap, USE.NAMES = !is.null(names(s)))
}
なんかを定義して使わないとダメみたいだ.
> capwords(c("abc", "xyz"))
[1] "Abc" "Xyz"
屋久島 MCMC 計算 (莫大な量) / 「直前」データ解析こんさる / 東京出張 / センター試験監督 / 統計学授業準備をこなせたのに, 今年は
屋久島 MCMC 計算 (ちょっと) / 「直前」データ解析こんさる / 統計学授業準備だけでへろへろしている. 嗚呼 ……
> (d <- data.frame(group = c(rep("a", 5), rep("b", 5)), x = rpois(10, 3), y = rpois(10, 9)))
group x y
1 a 2 7
2 a 0 9
3 a 3 14
4 a 4 15
5 a 4 12
6 b 1 8
7 b 3 7
8 b 5 12
9 b 1 11
10 b 9 6
このときに,
「group a, b ごとに y
の最大値の行を抽出して新しい data.frame 作れ」
という問題があったとしよう
(x 列は操作に何の関係もない,
しかし「捨ててはいけない」列である).
この例題だと見ればわかるように group a
に関しては 4 行め,
group b に関しては 8 行目をとってくればよい.
R にどう命令してやればそういう作業をやってくれるだろうか?
unlist(tapply(...))
使うと
> (s <- unlist(tapply(d$y, d$group, function(gy) 1:length(gy) == which.max(gy)))) a1 a2 a3 a4 a5 b1 b2 b3 b4 b5 FALSE FALSE FALSE TRUE FALSE FALSE FALSE TRUE FALSE FALSEこのように「どこに
group ごとの最大値があるのか」
がわかるような vector を作り,
あとはこれを
> d[s,] group x y 4 a 4 15 8 b 5 12とすれば「
group ごとに y
の最大値を含む行で構成された新しい data.frame」
が生成できる.
group
の並び順に注意!
あらかじめ sort しとく,
といった工夫が必要.
reshape()
が必要とわかり,
ちょっとじたばたする.