
[脱ダンボール寝生活めざして]
新春早々わけわかんない写真でごめんなさい
……

私の理解では,最大事後確率 (Maximum a posteriori; MAP) 推定値つまりモー ドを使うのが普通なのではないかと思います.なぜかといえば,これが最尤推 定値と対応しているように見えるからです.しかしながら,モードの推定は めんどうをともなうことが多いので,事後分布が「左右対称」っぽいのであれ ば期待値を使えばよいだろうし,期待値ではまずかろうという時には中央値が 使われているのではないでしょうか. ちょっとハナシがずれるのかもしれませんが,MCMC 計算を「モンテカルロ積 分」ととらえるなら,これは期待値を使うほうが普通になるんでしょうね.夜になってからの補足.
…… 使う目的とかにもよるんでしょうね.われわれにはあまり使う機会がないのか もしれませんが,事後分布が離散確率分布になるような問題 (例: ベイズ的画 像修復) なんかだと期待値よりも MAP 推定値を使うほうが自然なのかもしれ ません. 点推定的な発想は今後も必要とされるのかもしれません.Bayesian な論文な んかでも事後分布がどういうカタチであるのか,を (計算結果の Table など で) 表現するのに事後分布の 95% 区間だけでなく平均値や中央値を使うのは よくみかけます.
presentation.bib
はこんなかんぢで項目をならべていく.
@Misc{UseR2006,
Author = {久保拓弥},
Title = {{MCMC} 計算まわりでさまよう {R} ユーザー},
HowPublished = {統計数理研究所共同研究「Rの整備と利用」研究会},
month = {12 月 9 日},
year = 2006,
note = {統計数理研究所, 東京},
}
presentation.tex
はこんなかんぢで.
\documentclass[12pt]{jarticle}
\begin{document}
%\nocite{*} % データベイスファイル内の全部をだせという命令
\renewcommand{\refname}{\Large 口頭発表・ポスター発表}
\bibliography{presentation}
\bibliographystyle{junsrtKai} % 「引用」順
\end{document}
さて,
ここでもちいている junsrtKai.bst
なるスタイルファイルがいんちきなもので,
/usr/share/texmf/jbibtex/bst/junsrt.bst
(これは引用順に一覧を生成する bst ファイル)
を作業ディレクトリにコピーしてファイル名を改竄して,
年月日表示のところに手を加える.
FUNCTION {format.date}
{ year empty$
{ month empty$
{ "" }
{ "there's a month but no year in " cite$ * warning$
month
}
if$
}
{ month empty$
'year
{ year "年 " * month * }
if$
}
if$
}
われわれが普段お目にかかるプログラミング言語の中で
もっとも凶々しいモノのひとつ BibTeX style
定義言語については沈黙を守りたい.
Makefile
はこうなる.
junsrt (を改竄した bst ファイル)
を使っているので
bibtex ではなく jbibtex
を使わねばならぬ.
TARGET=presentation
dvi: ${TARGET}.dvi
${TARGET}.dvi: ./${TARGET}.tex ./${TARGET}.bib
platex ${TARGET} #1
jbibtex ${TARGET}
platex ${TARGET} > /dev/null #2
platex ${TARGET} > /dev/null #3
……
てなことを試行錯誤してるうちにできました.

dvi2tty
でテキストファイル
に変換して送信.



日本生態学会54回全国大会 一般講演 でご講演予定の 「屋久島照葉樹の葉寿命推定の階層ベイズモデル」 の要旨がまだ登録されていないようです.なるメイルが. わかってますって.
締め切り(2007年1月9日17時)が迫っています. ……
[glmmml] fail = 1 以下にエラーglmmML.fit(X, Y, weights, start.coef, start.sigma, fix.sigma, :といったエラーがでて計算してくれなくなることがある. こういったときは
glmmML(あれこれ, start.sigma = 2)などというふうに
start.sigma
値を設定してやるとうまくいく場合がある.
start.sigma
とは
sigma
の「最尤推定のための試行錯誤計算をスタートする時点での仮の値」
である.
じゃあ,
sigma
って何なのかと言えば,
GLMM
において「個体差」など random effects を表現させている
正規分布の「幅」のことで,
値の大きさが「個体差」の大きさをあらわしている.
start.sigma
を指定して計算させる場合,
start.sigma
の default 値は 0.5 なので
(help(glmmML)
参照),
0.5 より大きい値を設定してやる必要がある
……
最尤推定の収束計算がうまくいかない場合,
たいていは
start.sigma
が小さすぎるためだ.
glmmML()
になっても依然としてこの
start.sigma 変更わざ
が必要な場合があるんだな
……
ただし,
ちょっと試した範囲では,
以前とは異なり
start.sigma
によって結果がどんどん変わる,
といった悪しき事態にはなりにくそうな気がするんだけど
……?
BIOMETRY / jeconet reader 諸氏: 三中信宏です. 群馬大学の青木繁伸さんが〈R〉に関する教科書をオンラインで 公開されています. 青木繁伸 2006-2007 『Rによるデータ解析』(pdf) ダウンロード先およびサポートページ: http://aoki2.si.gunma-u.ac.jp/taygeta/Rstat.cgi 昨年暮れに初めて公開されましたが,その後も改訂が続いていて, 今朝ダウンロードしたものは「2007年1月3日版」で した. 詳細目次は私のブログに載せています: 青木繁伸『Rによるデータ解析』目次 http://d.hatena.ne.jp/leeswijzer/20061125/1164464145 ご参考まで.

d
をてきとうにでっちあげてみる.
> n <- 6 > d <- data.frame(value = 1:n, + x = round(runif(n, 0, 5), 1), y = round(runif(n, 0, 5), 1)) > d value x y 1 1 1.8 4.3 2 2 2.7 2.1 3 3 1.2 1.8 4 4 0.4 0.7 5 5 3.2 3.4 6 6 4.6 1.3こんなかんぢで,
d$x と d$y
が「点」の座標,
d$value
が「これに空間相関があるかどうか」を調べたいデータだとする.
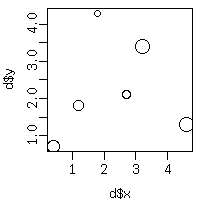
plot(d$x, d$y, cex = sqrt(d$value))
てなかんぢで.
> matrix.r <- as.matrix(dist(d[, c("x", "y")], upper = TRUE))
> matrix.r
1 2 3 4 5 6
1 0.0000 2.3770 2.5710 3.8626 1.6643 4.1037
2 2.3770 0.0000 1.5297 2.6926 1.3928 2.0616
3 2.5710 1.5297 0.0000 1.3601 2.5612 3.4366
4 3.8626 2.6926 1.3601 0.0000 3.8897 4.2426
5 1.6643 1.3928 2.5612 3.8897 0.0000 2.5239
6 4.1037 2.0616 3.4366 4.2426 2.5239 0.0000
r.star
より近い点は加重 1 で遠ければゼロ,
ただし距離ゼロ (つまり自分自身) も加重ゼロ,
としてみよう.
> weight <- function(r, r.star) ifelse(r < r.star & r > 0, 1, 0) > weight(matrix.r, r.star = 3) # 距離 3 未満なら 1, そうでなければゼロ 1 2 3 4 5 6 1 0 1 1 0 1 0 2 1 0 1 1 1 1 3 1 1 0 1 1 0 4 0 1 1 0 0 0 5 1 1 1 0 0 1 6 0 1 0 0 1 0
library(spdep)
の moran.mc
で 199 回ばかり Monte Carlo シミュレイションやってみる,
と.
> library(spdep)
> listw <- mat2listw(weight(matrix.r, r.star = 3))
> rndtest <- moran.mc(x = d$value, listw = listw, nsim = 199)
> rndtest
Monte-Carlo simulation of Moran's I
data: d$value
weights: listw
number of simulations + 1: 200
statistic = -0.0686, observed rank = 148, p-value = 0.26
alternative hypothesis: greater
観測データの Moran's I (距離加重つき相関)
は -0.0686 で,
これは「点の位置はそのままだけど d$value
でたらめに入れ換えました」無作為化 (randomization)
で得られたランダム化 Moran's I 分布の 95% 区間内に入っておりました
(p-value = 0.26)
なる結果でした,
と.
r.star
を変えていったときの観測値の Moran's I と
無作為化シミュレイションの 95% 区間
(rndtest$res に入っている結果を利用して計算できる)
を図示するプログラムとかも追加して
……
さてさて,
阿寒データ解析はこれにて終了か?
glmmML()
がすっかり
カシこく
なったことだし,
もはやこんな無駄な変換は世の中からなくなってくれても
よいと思うんだが.
data
という名前の data.frame をでっちあげる.
> (data <- data.frame(id = 1:4, n.sample = 5,
x = c(2, 5, 3, 4), y = c("red", "yellow", "green", "blue")))
id n.sample x y
1 1 5 2 red
2 2 5 5 yellow
3 3 5 3 green
4 4 5 4 blue
各行は「5 sample のうち x 個が『応答』しました」
といった二項分布モデルを使って解析したくなるデータセット,
と考えてほしい.
x 以外の列は無意味なでたらめ.
ただし id 列はあとで重要になる.
これの {0, 1} 変換とはこういうことで,
もともと 4 行だった data.frame を 20 行の data.frame になおすことである.
id x n.sample y 1 1 1 5 red 2 1 1 5 red 3 1 0 5 red 4 1 0 5 red 5 1 0 5 red 6 2 1 5 yellow 7 2 1 5 yellow 8 2 1 5 yellow 9 2 1 5 yellow 10 2 1 5 yellow 11 3 1 5 green 12 3 1 5 green 13 3 1 5 green 14 3 0 5 green 15 3 0 5 green 16 4 1 5 blue 17 4 1 5 blue 18 4 1 5 blue 19 4 1 5 blue 20 4 0 5 blueさて, これを簡単にやるにはどうしたらよいか, というまあ R の data.frame 操作練習, みたいに考えるか.
x
という列名の列を {0, 1} 展開して横に
ID となる列をくっつけ
merge() する
(ID にあわせて結合)
# data という名の data.frame を {0, 1} 展開する
n.repeat <- 5 # 展開する回数
colname.expand <- "x" # 展開する列名
colname.id <- "id" # merge でくっつけるときの id 列名
colnames.others <- colnames(data)
colnames.others <- colnames.others[ # colname.id 列を含む
colnames.others != colname.expand
]
converted01 <- data.frame( # id つき {0, 1} の長い data.frame
c(sapply(
data[, colname.expand],
function(x) c(rep(1, x), rep(0, n.repeat - x))
)),
c(sapply(data[, colname.id], function(x) rep(x, n.repeat)))
)
names(converted01) <- c(colname.expand, colname.id) # 列名をつけて
converted <- merge(converted01, data[, colnames.others], by = colname.id)
print(converted)
n.sample
(コード中では n.repeat)
が等しいのでこうなる.
行によって n.sample
が異なる場合はもう少し工夫が必要である
(参照: 前回の方式).
example(ranef)
は勉強になるというか,
ナゾにみちた
lmer()
の挙動の一端がよーやくにして少し理解できた.
これって単純に
formula
書いた場合の事前分布は一変量正規分布ではなく
多変量正規分布だったのか!
……
計算結果をよく見ていれば気づいてしかるべきだった.

[P1-155] 屋久島照葉樹の葉寿命推定の階層ベイズモデルは 3 月 20 日 (火) 12:00-14:00, か.