
[お茶部屋すけじゅーる板]
いつのまにやら院生の誰かが書いたもの.
これはきっと「いじめ」ではないのだろうと思う.
きっとそうにちがいない
……
ああ,
しかし精神的重圧感がのしかかってくる
……
BIOMETRY / jeconet reader 諸氏: 三中信宏です. 群馬大学の青木繁伸さんが〈R〉に関する教科書をオンラインで 公開されています. 青木繁伸 2006-2007 『Rによるデータ解析』(pdf) ダウンロード先およびサポートページ: http://aoki2.si.gunma-u.ac.jp/taygeta/Rstat.cgi 昨年暮れに初めて公開されましたが,その後も改訂が続いていて, 今朝ダウンロードしたものは「2007年1月3日版」で した. 詳細目次は私のブログに載せています: 青木繁伸『Rによるデータ解析』目次 http://d.hatena.ne.jp/leeswijzer/20061125/1164464145 ご参考まで.

d
をてきとうにでっちあげてみる.
> n <- 6 > d <- data.frame(value = 1:n, + x = round(runif(n, 0, 5), 1), y = round(runif(n, 0, 5), 1)) > d value x y 1 1 1.8 4.3 2 2 2.7 2.1 3 3 1.2 1.8 4 4 0.4 0.7 5 5 3.2 3.4 6 6 4.6 1.3こんなかんぢで,
d$x と d$y
が「点」の座標,
d$value
が「これに空間相関があるかどうか」を調べたいデータだとする.
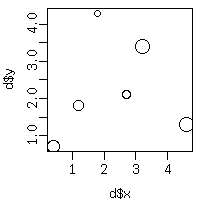
plot(d$x, d$y, cex = sqrt(d$value))
てなかんぢで.
> matrix.r <- as.matrix(dist(d[, c("x", "y")], upper = TRUE))
> matrix.r
1 2 3 4 5 6
1 0.0000 2.3770 2.5710 3.8626 1.6643 4.1037
2 2.3770 0.0000 1.5297 2.6926 1.3928 2.0616
3 2.5710 1.5297 0.0000 1.3601 2.5612 3.4366
4 3.8626 2.6926 1.3601 0.0000 3.8897 4.2426
5 1.6643 1.3928 2.5612 3.8897 0.0000 2.5239
6 4.1037 2.0616 3.4366 4.2426 2.5239 0.0000
r.star
より近い点は加重 1 で遠ければゼロ,
ただし距離ゼロ (つまり自分自身) も加重ゼロ,
としてみよう.
> weight <- function(r, r.star) ifelse(r < r.star & r > 0, 1, 0) > weight(matrix.r, r.star = 3) # 距離 3 未満なら 1, そうでなければゼロ 1 2 3 4 5 6 1 0 1 1 0 1 0 2 1 0 1 1 1 1 3 1 1 0 1 1 0 4 0 1 1 0 0 0 5 1 1 1 0 0 1 6 0 1 0 0 1 0
library(spdep)
の moran.mc
で 199 回ばかり Monte Carlo シミュレイションやってみる,
と.
> library(spdep)
> listw <- mat2listw(weight(matrix.r, r.star = 3))
> rndtest <- moran.mc(x = d$value, listw = listw, nsim = 199)
> rndtest
Monte-Carlo simulation of Moran's I
data: d$value
weights: listw
number of simulations + 1: 200
statistic = -0.0686, observed rank = 148, p-value = 0.26
alternative hypothesis: greater
観測データの Moran's I (距離加重つき相関)
は -0.0686 で,
これは「点の位置はそのままだけど d$value
でたらめに入れ換えました」無作為化 (randomization)
で得られたランダム化 Moran's I 分布の 95% 区間内に入っておりました
(p-value = 0.26)
なる結果でした,
と.
r.star
を変えていったときの観測値の Moran's I と
無作為化シミュレイションの 95% 区間
(rndtest$res に入っている結果を利用して計算できる)
を図示するプログラムとかも追加して
……
さてさて,
阿寒データ解析はこれにて終了か?