ぎょーむ日誌 2005-01-(21-31)

2005 年 01 月 21 日 (金)

• 0830 起床． アタマこわれぎみだな． 朝飯． コーヒー． また集団遺伝学とらっぷ． 1000 自宅発． 晴． 1010 研究室着．
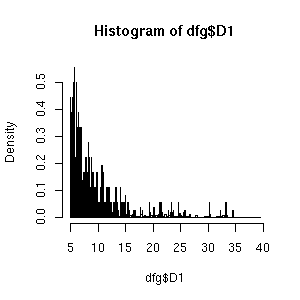
• なんかさー …… heterozygosity って， ようするに遺伝子の多様性ってのとおんなじですよねえ． で， 1 - Σi pi2 なる安直定義のせいで， ひどくあつかいづらい． だったらさー， 多様性をあらわせれば何でもいいっていうんだったらさー， heterozygosity なンかより Shannon-Wiener の情報量 Σi pi log pi のほうがよっぽど便利だと思うんだけどさー． 便利な理由: 個体内多様性・集団内 (個体間) 多様性・集団間多様性・ 「種間」多様性に分割可能だから．
• とゆーようなあたりの計算うだうだやって昼飯まえの仕事が終了． 昼飯． 粕谷さんからご指摘メイルいただく． うわっ， heterozygosity を heterozygocity などと書いていた． あわてて修正．
• で， Shannon-Wiener 情報量を遺伝学的多様性に使ったときの ご利益を確認する計算のつづき． かんたんなものなんだが， ひどく手こずる …… とゆーかですね， 計算まちがいだと思ってたのが， じつは意味のある結果になってたわけで．
• ある集団があったとして， それを構成する個体の個体内多様性 Hi' と 集団内多様性 H' が計算できたとしよう． Hi' にせよ H' にせよ， 「偏り」が少ないほうが多様性が高い， となる． では， 「個体間差異」をあらわす D = H' - E(Hi') はどうなるか? ここがぱっと理解できなかった部分で …… 得られた計算結果は「偏り」が大きいほうが D は大きくなる， ということを表現している． これもじつはあたりまえのことで， 遺伝子がどの個体にもひとしくばらまかれてる状態より， 偏りが大きいほうが個体間差が大きくなる， というだけのことだったわけで ……
• ともあれ， この計算方法で何重にも階層性をもつ多様性の構造を 単なる足し算に帰着できることが納得できた．
• 個体内多様性， という奇妙なコトバがでたついでに， 昨日の「無性生殖 (正確に言うとクローナル繁殖) する生物の heterozygosity 時間変化問題」 について考えてみよう． 有性生殖する有限集団はおそかれはやかれ heterozygosity はゼロに落ち込んでいく． そして， ここがちょっとパラドキシカルなところなンだけど， クローナル植物はその繁殖様式ゆえにゼロに落ちない場合がある．
• 極端な場合を考えてみればよい． ある集団が単一のクローンで構成されていたとしよう． このときに， そのクローン個体内部で着目する遺伝子座がヘテロ接合になっていれば? その集団は「みかけ上」高い heterozygosity を永久に維持するのである． つまり減数分裂などしない繁殖様式では， 個体内部という「避難場所」を得られるので， 集団の遺伝的多様性は高いまま維持される， ということだ．
• …… というようなことを検討してから， 本日の集団遺伝学相談． 立花さんは Shannon-Wiener 情報量に興味をもってくれたけど， 発案者たる私はそれで計算をぜんぶやりなおすことをおススめできづ． というのも， その路線でいくと 最終的にはモンテカルロ法をつかって 「どのレヴェルの多様性『差』が重要なのか」 を特定せんといかんわけで， 修論提出時期が接近しつつある現時点では無理っぽいからだ． そして多くの聞き手にとっては heterozygosity だろーが Shannon-Wiener 情報量だろーが， 「わけわからんけどそれっぽい」 ものであれば何でもいいわけで …… heterozygosity から派生するもろもろ統計量の でたらめと言ってわるければ無根拠計算あれこれ見てれば， そう思えてくる．
• 四倍体クローナルな集団のナゾの heterozygosity 問題は， 上述の「個体内多様性」を計算してみて， これで説明できそうか， というあたりでハナシをまとめることに． 「雑種強勢」とか見つかったりしたらおもしろいかもね …… ということで， あろざいむ集団遺伝学トンネル堀り的攻城戦も今日でひとくぎり， ということになるかな． すくなくとも， この古びた城の基盤の脆弱性はよく理解できるようになった．
• 2110 研究室発． 2130 帰宅． 体重 74.4kg． うーむ． どうしてこう重いのだろうか? 運動． 晩飯．
• おお． せとぎわぎみな季節 (in academic year) にふさわしいメイルがいくつか．
• [今日の運動]
  • エアロバイク 50 分間．
• [今日の食卓]
  • 朝 (0850): 米麦 0.7 合． タマネギ・ピーマン・ブナシメジ・豆腐のビーフシチュー．
  • 昼 (1320): 研究室お茶部屋． 米麦 0.7 合． タマネギ・ピーマン・ブナシメジ・豆腐のビーフシチュー．
  • 晩 (2340): 米麦 0.9 合． ワカメ・豆腐・卵の炒めもの．

2005 年 01 月 22 日 (土)

• 0830 起床． 朝飯． コーヒー． 洗濯． 怠業．
• heterozygosity は 1 - Σi pi2 なる定義のせいで計算めんどう， とか書いてたけど， やってみたら簡単にできた． というか， このあたり計算問題というより notation の整理の良否できまるんだよなぁ …… でやってみると下位と上位 (e.g. 個体と集団) の heterozygosity の差は …… homozygosity × (集団サイズ - 1)? なんぢゃこれは． 計算はあってるけど (後記: この計算はまちがい)， 意味不明だな． ということで Shannon-Wiener 情報量のほうがマシかも， ということで．
• 1530 自宅発． 雪． 半年ぶりぐらいに旭屋書店にたちよる． バクスター「真空ダイヤグラム」入手． 1650 研究室着．
• AMOVA 使えるかも， というご指摘うけて，

  Excoffier, L., Smouse, P.E. and Quattro, J.M. (1992) Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics, 131, 479-491.

  を読んでみる． 理解すんのに時間かかってしまったわけだが (こんなことやってる場合でもないんだが) …… いままで AMOVA (analysis of molecular variance) という名前と「分割表」しめすスタイルから， 世によくある 「なんでも ANOVA」 なる阿呆っぽい手口の亜流かと思っていたんだが， そうではなくなかなか面白い． ポイントは additive な遺伝的距離を定義するところで， これさえできれば線形モデルの問題に帰着できる．
• えー， しかしながらここ数日うだうだとやってた問題は， allozyme な頻度をとりあつかうもんなんで …… たぶん additive な距離を定義できないだろう．
• しかし， この著者の Excoffier なるヒトはハプロイドの最尤推定だの， 連鎖不平衡の尤度比検定だの， けっこういろいろと面白い推定計算法かんがえてるねえ． 生態学のデータ解析もせめて集団遺伝学のこういったのと同程度には おもしろくなってほしいもんだ．
• 2120 研究室発． 2130 帰宅． 晩飯．
• 苫小牧のほうの平尾君にその randomization ヘンじゃない， といったメイルおくってから， ようやくにしてなぜヘンなのか理解できた． いやはや …… なんというか自分で計算してないと， カンが働かないというかますます問題点がわからない， というか． このあたりはいらいらさせられる．
• [今日の運動]
  • 腹筋運動 30 × 3 回． 腕立ふせ 5 × 3 回．
• [今日の食卓]
  • 朝 (0900): 米麦 0.8 合． ワカメ・豆腐・卵の炒めもの．
  • 昼 (1400): マカロニ． タマネギ・ピーマン・ブナシメジ・豆腐のビーフシチュー．
  • 晩 (2240): マカロニ． タマネギ・ピーマン・ブナシメジ・豆腐のビーフシチュー．

2005 年 01 月 23 日 (日)

• 0830 起床． 朝飯． コーヒー． 怠業． 先週ばらばらと買ってしまった バクスター ``Xeelee Chronicle'' 文庫本 2 冊の表紙をならべてみるとえらくカッコよい (下の画像は Amazon からリンク経由の借用)． カヴァーイラスト / 撫荒武吉． どちらも抽象画に見えるかもしれないけど， きわめて具体的な情景を描いたもの． 青は青方偏移で， 赤は …… 死にゆく恒星たちの色か?

• 1220 自宅発． 晴． 昨日からの積雪は 1m を超えた． 1230 研究室着． おお， ストーヴつけっぱなしかと心配してたんだけど， そんなことなかったか． ひと安心して昼飯．
• ぱいぷ樹木原稿みなおし． しかし， 寒さと血糖値低下のせいかススまん．
• 1820 研究室発． 1830 帰宅． 体重 74.4kg． なぜかしら， 重いまま． 晩飯の準備．
• 晩飯くったら， いきなり寝てしまった． うーむ．
• [今日の運動]
  • いかん， 今日も運動休養日になってしまった ……
• [今日の食卓]
  • 朝 (0850): シリアル．
  • 昼 (1250): 研究室お茶部屋． セヴンイレヴン握り飯 & アサリ味噌汁．
  • 晩 (2000): 米麦 0.8 合． サバのショウガ煮． チンゲンサイ・マイタケ・豆腐の炒めもの．

2005 年 01 月 24 日 (月)

• 0800 起床． 朝飯． コーヒー． 0910 自宅発． 晴． 0920 研究室着．
• ぱいぷ樹木原稿なおし．
• なにやらおかしげな予算申請にまきこまれつつあり． またしても．
• 昼飯． 昼飯後に雪のふる中を農学部へ． ついでに北大生協で plotnet 面妖予算消耗のために購入された GIS ソフトウェアうけとる …… これがまた予想外に重くてかさばるハコで閉口した．
• 1300 より鍋嶋さんの D 論公聴会． 苫小牧でキビしい練習をへてきた， と思わせる内容でありました． 副査の一人， 甲山さんが論文原稿よく読んでない質問でもって 誠実なる講演者を困惑させたりするんで， 見てるほうがはらはらさせられる． 別のヒトの質問で「繁殖が直径成長に与える影響は?」 はありがちながら難問 …… 観測データないんで， これは「年」をランダム変量とするしかないかなぁ． 二重積分になっちまうが …… いや， 確率分布のたたみこみを利用すれば積分いっぱつでケリがつくか? 終了後， 鍋嶋博士 talk を聞くためにあちこちから集まった人たちと雑談．
• いったん研究室にもどってむちゃ重い GIS ハコを発注者たる 赤坂君のところにほうりこむ． 午前のへんてこ申請案件はそれほど危険性ないかも， というような情報が． しかしそれでも， わーど書類は提出させられることになりそう． いやはや． 1445 ふたたび研究室発． 外はあいかわらずの雪．
• 1505 低温研着． 低温研「ちゃらんけ」との 合同セミナー なんだが …… 地環研から来たのは合計 3 人． 本日は演題ふたつ．
• 一人目は低温研の原さん． いつもの 「日焼けは植物によくありません」 ハナシ． 北方林では幼木は光阻害死するからギャップ更新できないはず， というもの． しかも地球環境変動たるカムチャツカ乾燥化 (これがホントならこっちのほうが大発見なんだが --- 根拠は「氷河が後退してるから」だってさ) に促進された劇ヘンだとか． だったら， より水条件きびしく直射日光にさらされてる林冠木の葉群は なんでもっとぼろぼろにならないの? とつっこもうとしたら (これは誰にとっても当然の疑問なんで) 先に質問されてしまった． 明確な回答なくいづれ愛する分子生物学で解明する， とのこと． まあ， たぶんこのあたりはさまつなことで， 本講演のポイントは (これまた恒例) 合計 10 分以上ついやす 「自分にはたくさん友だちがいます」 投影資料たちの詳解だったのだろうけど．
• 二人目は無所属 (本人談) の小泉君で， オショロコマ のメタ個体群モデル， を構築できるよーなデータ集め・解析， そしてシミュレイションによる絶滅までの平均待ち時間計算． 「恩師」 前川さん の「釣人は良い研究者になれません!」断定の御真影つき引用から始まる． 遺伝子頻度の観点から「均質」と思われる複数局所個体群の変動が けっこうばらばら， というのは興味ぶかい …… がこの現象はそれこそ個体ベイスモデルとかで解析せんとわからんかも． 各集団で遺伝子組成が「違わない」ようにするプロセスが難しそう． 支流分断想定のもとでの絶滅評価シミュレイション， やけにわらわら破滅していくと思ったら， なんだか人工的に広域同調な環境振動もいれちゃったとのことで． ふーむ …… メタ個体群ねだやしにすんのはたいへんだからねぇ．
• また北大構内縦断して研究室にもどる． 時刻は 1720． また M2 立花さんと遺伝学相談． 四倍体は tetraploid とのこと (同型四倍体は autotetraploid)． 本日わかったこと． 2N vs 4N の heterozygosity 勝負は， haploid 無限集団が同じでも N が同じ有限集団なら 4N が常に勝ち． サンプル数多いってのと等価だから． そして大雪山中の 4N クローナル増殖集団は 「個体内多様性」が集団全体の ``heterozygosity'' 維持に重要だと示された． 立花さんのど根性ゑくせる手動計算にまちがいなければ …… どうしてよりによってゑくせるなんだろうね．
• 2110 研究室発． 2130 帰宅． 運動． 晩飯．
• [今日の運動]
  • エアロバイク 50 分間．
  • 腹筋運動 30 × 3 回． 腕立ふせ 5 × 3 回．
• [今日の食卓]
  • 朝 (0820): 米麦 0.7 合． チンゲンサイ・マイタケ・豆腐の炒めもの．
  • 昼 (1200): 研究室お茶部屋． 米麦 0.7 合． チンゲンサイ・マイタケ・豆腐の炒めもの．
  • 晩 (2210): 米麦 1.0 合． サバのショウガ煮． ダイコン・ブナシメジ・ワカメ・コンブ・豆腐の味噌汁．

2005 年 01 月 25 日 (火)

• 0820 起床． 朝飯． コーヒー． 今朝はなぜかしら三次元光分布問題にトラップされてしまう． 朝からアタマの中で三次元ヴェクトルがぐりぐりする． うう． 0940 自宅発． 曇． 0950 研究室着．
• まだ提出命令でてないんで， ぱいぷ樹木原稿なおしのつづき …… しかし， こんなもの読んでると， また今朝がた考えてた三次元光分布計算問題のうずに 巻き込まれていく ……
• で午前をぜんぶ思考迷宮の探索に費してしまって， またしても 新しい計算方法を考えついてしまった …… あえて名づけるなら 「光格子平面蚕食法，周期境界条件対応版」 とでもいうようなもので， 「見おろし法」の variation のひとつ． さして独創的ではない …… というか， ごくふつーのアイデアなわけで． いやはや， 私の場合，これまでのやり口が奇をてらうものばかり， と言えるのかも． たぶん， こっちの方式は誰かがすでに考えだしているだろう …… あるいはすでにふつーに使われているのかもしれない． ともあれ， 周期境界条件への対応が容易でそれなりに高速， メモリもむちゃくちゃに食いつぶすわけではない， と期待できそうな気もする．
• 昨年 3 月ごろには， 遮光物のほうを「回転」させる方法 なんぞを一生懸命かんがえてたわけだが ……

[去年 3 月ごろ考えてたやり口]

これって ずいぶんと手ぬきしてるんだけど， それでもけっこう大変なんだよね． いちいち座標変換して並べ換えてやらんといかんから．

• こういうかんぢではなく， また光線だの視線だのといった概念も とりあえず持ち出さずに， 「光子」を水平な格子平面上にならべておいて， その平面の水平をたもちつつある直線 (まあ，これは光線の入射角なんだが) にそって移動していけばよい． で， その光子平面が次第に「蚕食」されていく， と． どんなもんでしょね．
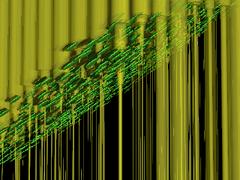
• ここに書いたら脳内から以上のアイデアをひとまずは消去できる， と思ったんだけど， なかなか消せん． 暴走してんのか? どこを押せば私は再起動するんだ? …… それはともかく， この方式はけっこうメモリを食いつぶすような気がしてきた． 三次元格子モデル になっちまうのか? これは 4-5 年前まで使っていて， いまは放棄したやりくちだ …… 調べてみたら kubolib20001014 が最後か． それの限界は このあたり のぎょーむ日誌に． ぱいぷ樹木には使えるかもしれんけどねえ．
• ぱいぷ樹木原稿なおしのつづき．
• 昼飯． 昼飯後に毎週の講座セミナーならぬ宣教師殿の 宣教せみなりお …… まぁ， とりあえず 3 週間後の修論発表会で， だれが不信心ものなのかすべて明らかになるんでしょう．
• ぱいぷ樹木原稿なおしがひと区切りついたんで， 印刷出力して共著者・甲山さんにわたす． Springer の batch 処理は遅々としてるよーで， 「はよだせ」督促はまだとのこと．
• で， インドネシアみやげをいただく． 下の図に示されてるよーな， 熱帯林 (カリマンタン島) 樹木の成長データ． うーむ， なんか面白いというかみょーなパターンが ……

• まあ， これは後日にやることにして， 1850 研究室発． 1900 帰宅． 体重 74.4kg． うーむ． 晩飯．
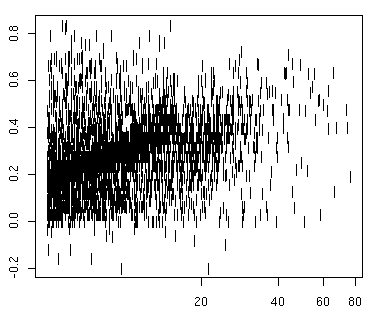
• なンとなく， また三次元光分布問題を考える． 三次元格子モデルは論外． STL の bitset 使っても無理だとわかった …… 1024 × 1024 × 1024 あたりが限界か． これで数百メガバイト使ってしまう (ま， データベイスとかランダムアクセスファイル， って方法もあるけどね)． とゆーことで …… 「光格子平面蚕食法，周期境界条件対応版」 なる方法つかうんなら， すべての遮光おぶぢぇくとは球， どの方向に射影しても円形に「蚕食」される， とするしかありませんなぁ． まあ， 「なにもかも球」 にしたところで近似的になってしまうけれど．
• しかし， 近似でもなんでもいいから， このあたりの計算を 100 倍 ぐらい速くせんことには， ぱいぷ樹木 は改良できん．
• [今日の運動]
  • エアロバイク 50 分間．
  • 腹筋運動 30 × 3 回． 腕立ふせ 5 × 3 回．
• [今日の食卓]
  • 朝 (0850): 米麦 0.7 合． ダイコン・ブナシメジ・ワカメ・コンブ・豆腐の味噌汁．
  • 昼 (1450): 研究室お茶部屋． 米麦 0.7 合． ダイコン・ブナシメジ・ワカメ・コンブ・豆腐の味噌汁．
  • 晩 (1930): 米麦 0.7 合． ダイコン・ブナシメジ・ワカメ・コンブ・豆腐の味噌汁．

2005 年 01 月 26 日 (水)

• 0830 起床． 朝飯． コーヒー． また三次元問題． やっぱ射影したら死ぬほど時間かかる． 1000 自宅発． 曇． 1010 研究室着．
• わけのわからん申請まきこまれ件の処理． が， その「様式」のたぐいは私が書くべきものとは どうしても考えられんので， その腐れわーどファイルを送りつけてきた方面に 再といあわせ …… しばらくしてから返信あったんだけど， どうやら先方が錯乱していたよーで． かかるどたばたぶりから憶測するに， このぷろぢぇくとはいよいよ採択されないような気がしてきた …… つまり私にとっては「安全」ということだ．
• いぜん査読した論文原稿の再査読． それほどきちんと改善されとらんような気もする． 途中でなげてしまって， 大阪大会 の宿泊予約 むろん自分でネット上で探索する …… なぜか心斎橋近辺に予約してしまった． いちおー， 3/27 (日) に移動， ということで． 電子化なんちゃら委員会はないみたいだけど． 大阪に 4 泊せんといかん．
• 自由集会 はなんと 11F でやるのか． なんかずいぶんと下界から離れてしまってるよーな ……
• えーと， 旅程確定しただけでは 出張関連の書類がだせないような気がしてきた (2/18 までに本年度の予算をぜんぶ消化できる 手はずを整える必要あるもんで)． 航空券を購入して領収書をだしてもらわんといかんのかしらん?
• 再査読のつづき．
• ズボンひざがいきなり破れる． しかもいかなる相互作用によるものか， 左右同時に． うーむ． 昼飯．
• 再査読のつづき． がイヤになったので大阪往復航空券予約 (予算処理には領収書が必要)． これは北大生協経由． 本日の教訓: イヤな再査読があると雑用処理が進捗する．
• いつまでも逃げてられないので再査読のつづき． 前回よんだ内容がいがいとアタマに残ってる …… ということで， 査読報告書きに着手． 1633 送信． 一件落着． ふう．
• ひざ破れがどんどん進行するんで， 北大構内走用のジャージを着用． 金属疲労ならぬ繊維疲労か?
• 甲山さんからのインドネシアみやげを始末することに． データにいくらか不審な点が． そのあたり確認するついでに， 甲山さんのところにいって成長量論争． 甲山さんは 「分散 = (平均)²」派 で私はそんなにでかいわけないでしょうという立場の 「分散 = 平均」派． ところがインドネシアデータは 「分散 < 平均」 なんだよね …… ふーむ．

[平均 vs SD]

集団を (ほぼ) 十等分割した計算結果．

• 1850 研究室発． 1900 帰宅． 晩飯．
• 苫小牧の平尾君の直前対策こんさるたんと， と上の平均 vs 分散関係を苫小牧直径成長データについて (いまさらながら) 確認しておく …… という「苫小牧な夜」 になってしまった．
• 計算中， 焦燥感で胃が痛くなったけど …… 直径成長データに関しては， 無事に 「分散 = 平均」 が確認できた． 苫小牧ボスに申しわけがたつ (安堵のあまり脱力)． 共同研究用 wiki にアップロード． そうだよな， このための「カウントデータ化」だったわけだし (overdispersion でるようなら負の二項分布にきりかえればよい) ……

[苫小牧直径成長 7 年分]

カウントデータ化した成長量， 個体ごとの平均 vs 分散． 「分散 = 平均」 のセンよりちらかってけれど， これは気象による年変動の影響によるもの．

• しかしもう一方の苫小牧寄生ハチ問題は …… どういう発表になるんだろーね． こないだの日曜日になってようやく思いついた 「autologistic model の最大 pseudo likelihood 推定値 (MPLE) の randomization test」 はなかなか面白い結果になったみたいなんだけど ……
• こんさるたんとメイル: 「……ここは丁寧に説明しなくてはなりません． 多くの生態学者はばらつきから情報をよみとる習慣をもたないからです ……」
• [今日の運動]
  • 腹筋運動 30 × 3 回． 腕立ふせ 5 × 3 回．
• [今日の食卓]
  • 朝 (0850): 米麦 0.7 合． タマネギ・エリンギ・卵の炒めもの．
  • 昼 (1320): 研究室お茶部屋． 米麦 0.7 合． タマネギ・エリンギ・卵の炒めもの．
  • 晩 (2030): 米麦 1.0 合． ネギ・マイタケ・卵炒飯． ワカメスープ．

2005 年 01 月 27 日 (木)

• 0700 起床． 朝飯． コーヒー． 0810 自宅発． 晴． 0820 研究室着． 輪読会の予習．
• 1000 より Life History Evolution in Plants 輪読会， 本日は第九章で担当は D2 西村さん． 内容は植物に感染する病気が植物の生活史にあたえる影響． ふーむ …… なんかけっこう動物のそれに似てるよな． 病気に操られたりするところとか． 1230 終了．
• 北大生協にいって書籍部うろうろ． 昼飯調達． クラーク会舘でそれを食ってから農学部へ． 今日はフィールドセンターの修論発表会で 苫小牧 な M2 のヒトたちも発表する． 皆さん， まあ無事に発表をこなして 1630 すぎに終了． 今日は動物のハナシばかりだったな． どれもなかなか面白いものでした． 北海道内数ヶ所にちらばる研究林のなかで， 苫小牧では局所的に一般化線形モデル (GLM) が普及しつつあるもよう …… しかし 「そこで『わりざん値』なんか使うとせっかくのデータが……」 といういくつかの研究については， 「わりざんヤメてこうやったらどうでしょう」 提案．
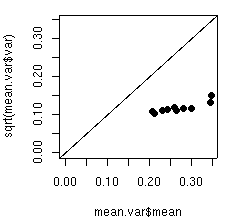
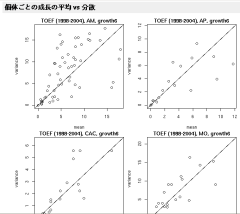
• すくなくともカウントデータ ({あり, なし} とか {0 個, 1 個, 2 個, ...} というふうに数えられるデータ) に関しては， データ解析上「わりざん」は まったく不要 (むしろ有害) と断定できる． 計測時間とかがそろってないなら， glm() の offset などつかえばよろしい．
• 連続値でもおそらく「わりざん」不要， と予測している． 比喩的にいえば， 生物は「わりざん」などしないのだから．
• 農学部発． 研究室にもどる． ばてたのか何も進捗せづ …… 1910 研究室発． 1930 帰宅． 体重 74.4kg． 晩飯の準備． 運動． 晩飯．
• [今日の運動]
  • エアロバイク 50 分間．
• [今日の食卓]
  • 朝 (0710): 米麦 0.7 合． ワカメスープ．
  • 昼 (1310): 北大生協サンドイッチ．
  • 晩 (2230): 米麦 1.0 合． ハクサイ・ジャガイモ・ニンジン・ブナシメジ・豆腐 のシチュー

2005 年 01 月 28 日 (金)

• 0730 起床． 朝飯． コーヒー． 0900 自宅発． 晴． 0910 研究室着．
• とりあえず， 甲山さんのインドネシアみやげデータの解析のつづき． いろいろと奇妙なことに気づいた．
  • 樹種によって観測インターヴァルが異なる …… 樹種内の個体間ではそろっている (?)
  • 樹種ごとに カウントデータ化した成長量をみると， みょーに分散が小さい (ような気がする)
  いや， 待て …… サイズを無視して平均・分散計算すると， 妥当に見える数値になった (6.13 vs 6.40)． 下の図はもっとも本数の多い (567 個体) Palaquium leiocarpum (アカテツ科 Gutta hang kang，樹液からゴムが得られるそーで)．

• えーと， ですね …… 上の樹種はたまたま「分散 = 平均」だけど， 全樹種 (147 種) でみると， 「分散 > 平均」 だな． ならば甲山さん提唱するように 「分散 = 平均²」 なのかというと …… そうではなく 「標準偏差 = 0.5 × 平均」 ぐらいか? ともあれ， この先は甲山さんにお尋ねしたほうがよろしかろう， というかんぢだ． 今日は出張か?
• 数日前のアヤしげ申請問題， とりあえず当方にとっては面倒が少なくなる方向に 転がりつつある． しかし， 今日中にヘンてこなケイ線書類ださねばならんそーで． 願わくば， これでこの一件は終了してほしい．
• 書類かくのイヤだなぁ …… とうだうだしてたら， 苫小牧の平尾君 (じつは本日も研究林修論発表会は続いていた) がやってきたんで， 雑用はほうりだして苫小牧寄生ハチモデリング相談． 昼飯をたべにでる．
• あきらめて書類仕事． 記載事項のテキストファイルをつくり， それを研究室内の共用ゐんどーづ機で切り貼り． 送信． 一件落着， と脱力してお茶部屋に逃げると， そこに新たな災難が …… とある偶然がつみかさなり， お茶部屋でアマチュアのアイヌ研究者のご高説を 30 分間起立したまま拝聴することに． 元気な (というか明らかに軽躁気質な) ご老人で古事記・源平合戦・元寇・関ヶ原合戦といった日本史の理解に アイヌは必要不可欠という持論が (ひどく短い lag で消失する時間的自己相関によって) うねる …… 自分の知識の連鎖を楽しむ熱心な dilettante にも見えるし， しゃべったコトバ自身がそこまでの脈絡をすぱっと切断していくさまは 境界線上のヒトなのかしらんという気にもさせられるし．
• ばてた． 私もそうとうにヘンなのだろーけど， ご老人も少なくとも同程度にはおかしい． そこで思いついた仮説: アタマのヘンな人間は 自分と同程度かそれよりヘンなヒトの長話をきかされると ひどく疲れてしまう．
• またお茶部屋で今年の進化植物研究会雑談．
• 出したはずのメイルについて「まだ届いてない」通知いただく． しかもそれの配信も一時間遅れで． もしや， と思って調べてみたら …… やれやれ， またまた北大ネットがやってくれましたよ．

  	2005年1月28日、17時現在、北大内メールシステムに障害が発生しています。
  	現在、復旧作業中ですのでしばらくお待ちください。
  	↓
  	18時頃、配信処理を再開しました。
  	障害中に配信されてきたメールは随時処理中です。
  

  だってさ (これらの文言は学外から見えないところに隠蔽されている)． 「障害」の実態は内外やりとりがほぼ完全に停止． 「17 時現在」 とかごまかしているけど， ぢつは遅くとも 16 時には壊れていたわけだが …… まあ北大ネット独特のいんちき表記ということで． 「随時処理中」はまったく信用できんので， 別経路で送りなおす．
• 一番最初に送られてきた一番重要なメイルが一番最後になって 配信されてきたりするし …… どーして， こう管理者の連中はいつもいつも同じような失敗ばっかりやってんのかねぇ．
• というようなことの始末にわずらわされてから， 2020 研究室発． 2030 帰宅． 晩飯． いきなり寝てしまった．
• [今日の運動]
  • 期せずしてうんどう休養日．
• [今日の食卓]
  • 朝 (0830): 米麦 0.7 合． ハクサイ・ジャガイモ・ニンジン・ブナシメジ・豆腐 のシチュー
  • 昼 (1240): 百周年記念館「きゃら亭」昼定食， シーフードオムレツ．
  • 晩 (2100): 米麦 1.0 合． ハクサイ・ジャガイモ・ニンジン・ブナシメジ・豆腐 のシチュー

2005 年 01 月 29 日 (土)

• 0940 起床． 朝飯． コーヒー． 洗濯． 怠業． 怠業．
• 昼飯くってから 1320 自宅発． 曇というか雨? 気温高い． 1330 クラーク会館地下 理髪店． こんでたので本など読みつつ一時間ほど待つ． 散髪そのものは 45 分ほど． 2625 円． 1530 研究室着．
• 図書館でかりてきた 柳川ノンパラメトリック本 読み (これまた絶版本なんだけど)． 以前から 粕谷さんご指摘 しておられるように， 「母分散が等しくないとき」 Mann-Whitney U 検定など位置パラメーターの検定はできない (通俗的統計学本とかで 「不等分散でもノンパラメトリック検定できる」 などとあるのはまちがいである)． で， 柳川本を読んでみていまさらながらにして， その理由が理解できた．
• 順位統計量にもとづく検定というわくぐみそのものは， 必ずしももと集団に等しいばらつきを常に要請しているわけではない (尺度パラメーターに関する Siegel-Tukey 検定などもある) …… では， なぜ分散ひとしくない集団から得られた二標本に Wilcoxon だの Mann-Whitney だのの検定ができないのか?
• 答えは簡単で， 位置パラメーターに関する 検定統計量の危険率の計算， 言うところの P 値の数値計算の実際の手順において 「母分散は等しい」 を大前提としているからである． したがって， どうしても不等分散状況化で位置パラメーターの ノンパラメトリック検定やりたきゃ， そういう状況に合致した P 値計算方法を考案すればよろしい， ということになる． ま， 無理だろうけど (…… と書いてしばらくしてから「条件付さんぷりんぐ?」 というコトバが脳内で明滅した)． あ， 「大標本数のもとでの統計検定量の正規分布近似」 なんて手口もあるから， それを不等分散にしてみる? もう何やってんのかわけわからんね．
• というふうに， 生態学の統計学的データ解析における 旧来的な (比喩的に言えば， 巻末 P 値表を参照するような) ノンパラメトリック検定はオワっていくのでありましょう (一部の敬虔なる「のんぱらめとりっくは万能」信者たちをその道づれにしつつ)． むろん bootstrap な方法あれこれは これからも使われつづけるだろうし， また別の「分布の関数型を特定しない」方法 (おそらく最尤法などにもとづく) もいろいろと試されていくんだろうけど．
• 1840 研究室発． あいかわらず雨． 先日ズボンやぶれたんで東区北 7 のユニクロで替えを調達． これはけっこうみじめな体験というか …… 胴まわり 85cm ぐらいなんだけど股下 79cm というところで (蛇足ながら身長は 177cm)， 後者のほうが短いってのはひどくまぬけな気にさせられる． 1990 円 × 2 本．
• その店の横にけっこうでかい Book-off があるのを発見． のぞいてみる． 札幌市東区区役所周辺って， JR 札幌駅から直線距離で 1000m ぐらいしか離れてないのに， こういう「郊外型」の土地の使われかたしてんだよね． 歩道車道せまく除雪された雪が堆積して山道のごとく 細くなって起伏が生じた道を上下しつつ (最後に創成川をざぶざぶと渡渉して) 北区にたどりつく． 2100 帰宅． 体重 74.2kg． 晩飯．
• [今日の運動]
  • 腹筋運動 30 × 3 回． 腕立ふせ 5 × 3 回．
• [今日の食卓]
  • 朝 (1000): リンゴ．
  • 昼 (1300): スパゲッティー． ハクサイ・ジャガイモ・ニンジン・ブナシメジ・豆腐 のシチュー．
  • 晩 (2200): 蕎麦． ワカメスープ． モヤシ・ピーマン・ニラの炒めもの．

2005 年 01 月 30 日 (日)

• 0810 起床． 朝飯． コーヒー． いかん， また怠業．
• 1240 ひさびさの北大構内雪上走． 晴． 気温は低く耳が凍傷になりそうだ． 冬の平日に走らないのは滑るから， ではない (気温が氷点下のときに凍結した路上は滑らない)． 除雪によって歩道幅が半分ぐらいになっており， そこをえっさえっさと走るのは他のヒトたちの迷惑になるからだ． 土日なら問題なかろう …… というのも構内の車道を走ればいいからだ (北大構内であっても平日にこれをやるのは自殺行為)． 軟雪あるところを選んでコースをとる． 1325 帰宅． 体重 74.2kg．
• 昼飯くってから 1500 自宅発． セーターをクリーニングにだす． 294 円． 晴． 1515 研究室着．
• なぜかまだ続いているぱいぷ樹木原稿ばぐ出し． まだ間違い発見できる． いやはや．
• ひと区切りついたんで 2040 研究室発． 2050 帰宅． 晩飯．
• ガスファンヒーターだが …… たしかに便利だけどガス代もかさむ． いつもは毎月 2000 円ぐらいなんだけど， 今月は 5800 円だった．
• [今日の運動]
  • 北大構内雪上走． 45 分間．
  • 腹筋運動 30 × 3 回． 腕立ふせ 5 × 3 回．
• [今日の食卓]
  • 朝 (0840): パンケイキ．
  • 昼 (1400): ゴマ・ワカメうどん．
  • 晩 (2200): 米麦 1.0 合． モヤシ・ピーマン・ニラの炒めもの． ハクサイ・ネギ・ナメコ・ワカメ・コンニャク・豆腐・煮干の味噌汁．

2005 年 01 月 31 日 (月)

• 0730 起床． 朝飯． コーヒー． 0850 自宅発． 曇． 0900 研究室着．
• 今日明日は D 論発表の日 (当講座ぶんは明日)． 今日の午前中は 東研 の平田君 (コハナバチの真社会性・単独性の種内分化の地温依存性) ・城所さん (キオビツヤハナバチの訪花パターン，越冬前・越冬後交尾)． なんと言いますか， 「ハチ学」わーるどと言うか， ハチのふるまいについては理解がススんだ， というのはわかる． 今日のようなハナシを聞いてて気づいたんだけど， 私の場合， 生き物を「個体数の変動」とか「繁殖成功」みたいな量で理解しよう， という傾向に偏ってるんで， そういうデータとるのが難しい生き物の研究だと全体像がよく見えない． むろんそうでない世界もあるわけで …… 学外からも来たハチ学者たちと発表者のやりとり見てると， アチラの世界ではこういうふうに進歩が積みあがっていくんだろうなぁ， と想像はされるんだけど．
• 昼飯くってるうちに， だんだんばててきた …… というのも， 昨晩さっさと寝なくてはと考えてたのに， こういうときにかぎって読書に没頭してしまって， ですね． 睡眠時間 5 時間ぐらい． ホントにへろへろしてきた．
• 苫小牧ボスからいろいろご教示 & ご質問メイルに， 御礼と回答メイルかいてたるうちにも ふらふら感が …… これは危ないとお茶部屋に逃げると， お茶部屋 Mac で森兄弟真冬 New York 突発旅の すらいどしょーやってて， それを見てたらますますふらふらしてきた．
• M2 平林さん訪花データ解析プログラムの小改良 …… が必要かと思ったんだが， よくよく見てみたら何も変更しなくても現状のままで 新たに生じた計算需要に対応できるとわかった． それを平林さんに報告して一件落着．
• ぱいぷ樹木原稿ばぐ出し． ぢりぢり
• ひと区切りついたんで 1810 研究室発． うおや一丁 で plotnet に来た皆さんと北海道な魚介． よくしゃべるヒトたちに包囲されてしまった． 北山さんから Bond (1989) ``slow seedling hypothesis'' など教えていただく． 清野さんからは， ちかごろ興味もっておられる ``幹内の貯水'' その影響とみられる time lag の観測について， というあたりのハナシとか． 2120 帰宅．
• [今日の運動]
  • うんどう休養日．
• [今日の食卓]
  • 朝 (0800): 米麦 0.7 合． ハクサイ・ネギ・ナメコ・ワカメ・コンニャク・豆腐・煮干の味噌汁．
  • 昼 (1320): 研究室お茶部屋． 米麦 0.8 合． タマネギ・ピーマン・ブナシメジ・豆腐のビーフシチュー． 金曜日に凍結させといたやつ．
  • 晩 (1830): うおや一丁 で plotnet に来た皆さんと北海道な魚介．