ぎょーむ日誌 2004-12-(01-10)
2004 年 12 月 01 日 (水)
-
0920 起床.
うーむ
……
朝飯.
コーヒー.
しかも昨晩つくった作図プログラムまちがってるし.
再修正.
アップロード.
1040 自宅発.
曇.
1050 研究室着.
-
いかん.
生活周期が.
-
北大ネットの不調,
よーやく情報が少しでた:
本日午後から北大外への
webアクセスに遅延が発生しております。
原因は学内にある複数台の端末が
ウィルスなどに感染しているものと思われます。
……
だってさ.
今さら言われるまでもなく,
北大構内 LAN は virus の一大繁殖地になってしまっている.
virus 保全運動でもやってるつもりなのかね.
-
どれから着手すべきか
……
という逡巡.
とりあえず,
間瀬さんから
送っていただいた論文のコピーを読んでみる.
どうもいろいろな方面で
有名
なものらしい.
-
で,
関係ない勉強に走ってしまう.
いままでよくわかっていなかったごく単純なことが,
ひとつ理解できた.
データ解析用のニューラルネットワーク (NN)
の出力部分は自分で好きなように
設計してよい
……
これってネット上でぱらぱらとみた解説なんかには
どこにも書いてないんだけど
(あたりまえすぎるから?),
理解としては間違っていないだろう.
-
つまり NN そのものは非線形なモデルを表現するわけだけど,
最後の出力にもっていくところでは線形モデルになっている
(このあたり苫小牧直径成長モデルと同じだ).
つまりこの部分は
線形モデル・一般化線形モデル・一般化線形混合モデル
のたぐいとして扱えばよい.
たぶん,
尤度にもとづく一般化されたバックプロパゲイションなんかも,
誰かがすでに定式化しちゃっているだろうな.
うーむ,
急に目の前がひらけたような気がする.
-
しかし一番簡単そうな事例についてアタマの中で検討してみると
……
これって,
単に尤度関数を Newton 法のたぐいで最大化しました,
という問題とまったく変わるところがないな.
うーむ.
まあ,
私の中でそのあたりの整合性がつけられたのは
良いのかもしれないけど.
-
というようなわき道から論文よみにもどる.
集団動態を扱う生態学モデルでは,
いまだに平衡常態まわりの局所安定性なんぞという
理論的には退屈で
現実の系にはあまり使いものにならん「安定性」なんぞを
うだうだと検討したりする状況がつづいているわけだが
……
むしろシステムの安定性といったものを,
このような確率分布
(ここではべき乗分布 --- power low というやつ)
で表現するほうが,
理論的にも応用的にもご利益が多いような気がする.
-
科研費で購入をもうしこんだ書籍のうち,
とりあえず北大書籍部在庫のものがとどく.

[統計学本がメイン,か]
すでに持っているけれど,
研究室お茶部屋「統計本コーナー」に置くのも買った.
これでそちらに抑留されている自分の本を
連れ戻すことができる.
-
昼飯.
露崎さんによると,
Ecological Research は著者に
「査読して下さい」
メイルを送りつけるそうだ.
-
その Eco.Res. が浦口さんカエデ論文の proof pdf
ファイルを準備したというんで,
私も読んでみる.
意外にも,
というか出版社が変わった効果なのか,
数式まわりがかなり正確だった.
-
また論文よみのつづき.
-
するとこれを送っていただいた
間瀬さん
からメイルいただく.
じつはまだだった御礼を書いたりしてるうちに
……
東工大の研究室で検討されているという名字のべき乗分布 (?)
ってのは,
じつは熱帯多雨林の樹種共存の中立説 (Hubbell)
なんかでも生成できそうで,
しかもモデルとしての対応関係もいいのでは,
と気づいた.
ちょっと面白いかもしれないので,
私のメイルの一部を引用してみる.
名字の分布はごく単純に考えると佐藤・瀬野本 (じつは未読) のごとく
branching process でモデル化してよさそうです.しかし,もし名字の分布が
幾何分布ではなくべき乗分布になるのでしたら,どういう確率論的モデルでこ
れが生成・維持されているのか興味ぶかいところです.日本人を増殖・移動・
死亡する動物個体の集団と考えると,これらの各過程がどうなっていたら,名
字 (動物個体の中立的な遺伝子マーカーのごときものですね) の分布がこうなっ
てしまうのか,まず生態学的にはここが興味ぶかいところです.
突然,森林生態学に話がうつります.Steve Hubbell (「あの」Hubbell です!)
は生態学業界では「熱帯多雨林では樹種間に優劣がない→だからあんなに多数
の樹木種がいるのだ」理論の提唱者として有名です (熱帯多雨林の中立説).
樹種間に優劣がない(中立である) と言うのは,つまり「樹種名」というのは
樹木個体にはりつけられた無益・無害なラベルにすぎない,ということです.
そしてこの樹種 (あるいは樹種名) の分布は (じつは熱帯にかぎらず) 幾何分布には
「ならない」ということが知られています.私のいいかげんな記憶では,たしかべき
乗分布にむしろ近かったはずです.
Hubbell たちはこのような分布を生成する確率モデルを以下のように過程しま
した.
・森林はいくつもの小森林に分割できる.
・各小森林には有限個 (数百ぐらい?) の樹木個体が占拠できる場所がある.
・各小森林内ではときどき樹木が死に空き地が生じる.
・この場所とりに関して,樹種間では能力的な差はない (中立).
・生じた空き地を樹種 x が占める確率はその小森林内での樹種 x の頻度に比
例する (小集団での branching process).
・小森林間では「ときどき」樹木個体の行き来がある
(「空き地」が生じたときに,その小森林の「外」から樹木が侵入する)
といったものです.これで,現実に近い「樹種」分布が生成・維持できる,と
いうのが Hubbell の近著
The Unified Neutral Theory of Biodiversity and Biogeography
Princeton Univ Pr; ISBN: 0691021287 ; (2001/05/01)
で使われているモデルです (じつはこの本も未読なのですが……).ただし,
このモデルと分布の対応関係は,「こういうパラメーターでシミュレイトした
ら,このような分布がでた」ぐらいのことしか調べていないのではないか,と
思います (それで十分なので).しかし,他のべき乗分布を生成するシステム
との対応も知りたいところです.
話を日本人の名字にもどしますと,いくつかの地域に分割できる,地域内の人
口収容力はそれほど大きくない,名前は「中立」 (たとえば久保という名字だ
からといってたくさん子供を産んだりするわけではない),(近ごろはともかく
昔は) 人の行き来はそれほど頻繁ではなかった,というふうに,上の森林モデ
ルと符合している部分があるのかもしれません.あるいは,非常に単純なモデ
ルですから,名字分布モデルに関してもすでに誰かが Hubbell 的なモデルを
提案しているかもしれませんね.
といった勉強だけで一日が終ってしまった
……
1950 研究室発.
2010 帰宅.
体重 73.6kg.
晩飯.
明日の輪読会の予習.
[今日の素読]
-
Reekie, E.G. 2001.
Resource allocation, trade-offs, and
reproductive effort in plants.
in
Life History Evolution in Plants
(Timo Olavi Vuorisalo and Pia Kristina Mutikainen eds).
Kluwer Academic Publishers.
[今日の運動]
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
[今日の食卓]
- 朝 (0950):
シリアル.
- 昼 (1430):
研究室お茶部屋.
米麦 0.8 合.
チンゲンサイ・タマネギ・豆腐の炒めもの.
- 晩 (2130):
米麦 1.0 合.
キャベツ・ダイコン・サバぶしの味噌汁.
さつまあげ.
2004 年 12 月 02 日 (木)
-
0800 起床.
朝飯.
コーヒー.
輪読会予習の続きに没頭してしまう.
0920 自宅発.
曇.
0930 研究室着.
-
1000 より
Life-history evolution in plants
輪読会.
今日の担当は M2 堀端君で第 5 章
Resource allocation, trade-offs, and
reproductive effort in plants
(E.G. Reekie).
なかなか隠匿度の高い紹介だったけど,
隠匿点を指摘したときに師匠たる小菅せんせーのごとき
逃走能力がないので暴露してしまう.
-
で,
こういう本では簡単な数式で表現される概念モデルが
よく出てくるんだけど,
一般に当講座の院生たちはこれがとても苦手である.
というのも,
式を見てもグラフの概形が思いつかないらしくて,
ですね.
本日は,
院生そうがかりで
「y = a + b / x ってどんなグラフだっけ」
と一生懸命に試行錯誤する様子を観察してしまった
……
このあたり個体差は大きいので,
この標本だけで集団全体の傾向については推測できない.
しかしながら,
私は近ごろになって
「理系院生だからといって,
必ずしも中学・高校の数学が身についてるとは限らない」
という現象を現象論的に受け入れつつある.
1330 終了.
-
昼飯.
しかし考えるまでもなく,
院生と「これ,
どういう統計モデルでデータ解析しようかねえ」
などと相談してるときに,
私と先方の間でもしかしたらかなり認識にへだたりがあるかも,
という可能性は常に慎重に検討する必要あり,
ってことだよねえ.
-
「日替わり」北大ネットとらぶる.
12月1日(水)夕刻から、北大外から北大内に送信されたメールが正常に配信されて
いない症例が多数報告されております。現在、原因を調査・復旧作業中です。ご了承
ください。
↓
北大ネットワークシステム内のサーバ不具合により発生していたと思われる上記の症
状は、12月2日(木)12時 15分頃に復旧致しました。昨日の不具合発症以降に北大内
に向けて送信されたメールは随時、配信されておりますが、送信元メールサーバ(北
大外)の配信不達時の再送信実行時間が短く設定されている場合は送信者に向けて不
達通知が送信される場合があります。(メールが消失する等の症状は無いものと思わ
れます)
そして本日午後も統計学勉強だけで終ってしまった.
勉強はススむが,
仕事はススんでいない.
1830 研究室発.
1840 帰宅してから
自宅「うら」の北 12 生協に買い出し.
米 10Kg を運搬するには,
いったんデイパックをからにする必要あるもんで.
いつも 3000 円弱の道産米がなぜか 3700 円超.
茨城県産コシヒカリがそれよりびみょーに安かったので
そちらを.
10% 割引券使用.
晩飯.
[今日の運動]
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
[今日の食卓]
- 朝 (0820):
米麦 0.8 合.
チンゲンサイ・タマネギ・豆腐の炒めもの.
- 昼 (1350):
研究室お茶部屋.
米麦 0.8 合.
チンゲンサイ・タマネギ・豆腐の炒めもの.
- 晩 (2040):
米 1.0 合.
キャベツ・ダイコン・豆腐・サバぶしの味噌汁.
さつまあげ.
2004 年 12 月 03 日 (金)
-
0700 起床.
朝飯.
コーヒー.
朝から空間統計学 &
モンテカルロ法解決な問題の検討に没頭してしまう.
0850 自宅発.
曇.
0900 研究室着.
-
だー
……
パラメーター推定問題に没頭していたので,
ThinkPad の AC アダプターをまた自宅に置き忘れてしまった.
あとで取りに行こう.
とりあえず電池駆動.
-
冬といえば統計学こんさる
……
しかしながら,
良いこともたくさんある.
本日は東北大の
松島さん
に dispmod
package の存在を教えてもらった.
いつもながら,
大学院生たちの
CRAN
探索能力には驚かされる
(私はこのあたり苦手なもんで).
-
これには
glm.binomial.disp()
や
glm.poisson.disp()
といった関数が含まれておりそれぞれベータ二項分布
とガンマポアソン分布
(……って負の二項分布つまり glm.nb()
in MASS package と同じぢゃん! と今ごろ気づいた)
の推定計算をやってくれる.
で,
問題点は glm() の quasi-
family や glm.nb()
と同様にランダム変量の「いれかた」に柔軟性がないこと
(ポアソン分布について言えばこれは glm.nb()
でも同じ).
このあたりの久保コメント.
しかしながら,生物学関係で観察される現象は overdispersion になってる事
例も少なくないので (underdispersion の場合もあります),glm...disp() を
使うのはひとつの方法でしょう (他にもいろいろあります).
じつは私は松島さんに教えていただくまで,この dispmod package の存在を
知りませんでした.ご教示いただきありがとうございます.こういう問題のと
き,これまでどうしていたかというと,擬似尤度法を使う
glm(..., family = quasibinomial(),...)
glm(..., family = quasipoisson(),...)
あるいは glmmPQL() 関数 (in MASS package) を使うか,あるいは混合モデル
の最尤推定 glmmML() 関数 (in glmmML package) を使うか,あるいは自分で
問題にあわせた新しい関数を書いていました.
いろいろな方法を列挙しましたが,dispmod の関数たちの利点は
overdispersion 表現する混合モデルを最尤法でお手軽に計算できること,欠
点は「ポアソン分布や二項分布を超えたばらつき」(ランダム変量と呼んだり
します) の入れかたに柔軟性がないところでしょうかね.
時刻は 1040.
電池残量 40%.
残りの推定稼働時間 1 時間 6 分.
いつまでも仕事をさぼってるわけにもいかんので,
アカマツ作図宿題にとりくむ.
と思ったら電池残量 5% 警告.
時刻は 1123.
加速度的に消耗するのか?
いったん suspend.
それを口実に仕事をさぼり,
また統計学勉強.
ぢつは,
混合モデル → ベイズモデル → MCMC で解決,
ってそんなに見通しがよくないのか?!
などとうろうろしてると,
甲山さんがふらふらと徘徊してきたので,
統計学雑談.
昼飯.
昼飯後にいったん帰宅して AC アダプターを取ってくる.
ThinkPad X31 復活.
suspend してるときの電力消耗は 1 時間に 1% ぐらいか?
うーむ,
簡単な作図問題なんだけど
……
進捗しない.
不調.
……
するとすぐに統計学勉強に逃避してしまう.
今度は R
実践編.
うーむ,
じつは
MCMCpack
なる package があったのか
(cf.
http://mcmcpack.wustl.edu/
).
インストールするには
coda
をあらかじめインストールする必要あり
……
などと R 世界にかまけていると,
いきなりお茶係の女性大学院生から
「お茶代ください」
奇襲攻撃をくらい,
ぼうぜんとしてるうちに現金を持ち去られてしまった.
さーて,
この
MCMCpack
中の
MCMClogit()
だの
MCMCpoisson()
だのといった関数どもだけど
……
これらは何か実用的な関数というより,
MCMCpack
利用するプログラムはこう書け,
というような example の意味あいが強いのではないか?
試運転の結果などはまた明日.
ということで,
本日も統計学文献よみと MCMCpack
とりつきで終わってしまった.
うーむ,
危険だ.
1920 研究室発.
1930 帰宅.
体重 73.2kg.
晩飯.
[今日の運動]
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
[今日の食卓]
- 朝 (0730):
米麦 0.8 合.
キャベツ・ダイコン・豆腐・サバぶしの味噌汁.
- 昼 (1250):
研究室お茶部屋.
米麦 0.8 合.
キャベツ・ダイコン・豆腐・サバぶしの味噌汁.
- 晩 (2030):
米麦 0.8 合.
キャベツ・ダイコン・豆腐・サバぶしの味噌汁.
2004 年 12 月 04 日 (土)
-
0830 起床.
朝飯.
コーヒー.
-
朝から,
昨日のつづき,
MCMCpack
調査にとりくむ.
これも一種の怠業に他ならない.
-
とりあえず,
定数項が正規乱数になってる
normal logit model の推定問題.
乱数生成&推定&作図のプログラムは
これ
(
glms.R).
推定結果などは
これ
(glm.txt).
-
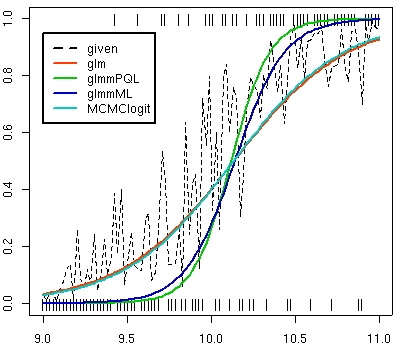
上の図はよくでる推定結果パターンの一例
(これはたまたま
glm()
と
MCMClogit()
の推定結果が良かった場合).
一番単純な一般化線形モデル
glm()
と
一番複雑な MCMC ベイズ推定の
MCMClogit()
の結果がだいたいいっしょで
(glm(..., family = quasibinomial)
は推定値に関しては
glm()
と常にまったく同じ),
罰則つき擬似尤度法
glmmPQL()
は「傾き」のキツすぎる推定結果をだし,
最尤法による一般化線形混合モデル推定
glmmML()
はそこまではキツくない結果になる.
-
他によくでる結果の例としては
-
どれでやっても同じ
(どれも同じように良い,
もしくはどれも同じように悪い).
-
glmmPQL()
だけが異なる
あたりかな.
ただし,
最尤法な
glmmML()
はそもそも収束計算をしくじることが多く,
もっとも不安定な推定計算方法と言える.
-
で,
わざわざ MCMC 法使っていながら,
しかもわざわざパラメーターにばらつき持たせている状況でありながら,
MCMClogit()
の結果はよろしくないような.
何度やっても,
こういったばらつきをまったく考慮しない
glm()
とほとんど同じ推定結果になるんで,
これだったらベイズ推定とかやる御利益とか
何もないぢゃん.
-
まあ,
この例題があまり適切でなかったかも,
という可能性はあるにしても,
だ.
-
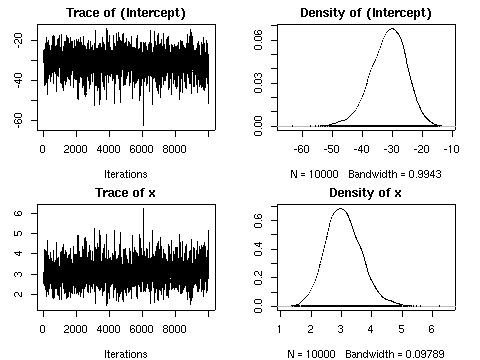
MCMClogit()
の出した事後分布.
この事例ではたまたま推定値の平均はそれっぽい値になっているけれど,
いっぽうで
variance がむちゃくちゃでかいんですけど
……
-
昼飯.
しばらく R でうだうだしてから
1430 自宅発の北大構内走.
曇天.
しかし夜間にふった雨のおかげで雪はかなりとけている.
1530 帰宅.
体重 72.8kg.
-
1630 自宅発.
すでに夜.
曇.
1700 研究室着.
-
動物行動学会大会
でお疲れの
粕谷さん
からご指摘メイルいただく.
昨日のぎょーむ日誌に書いた,
glm.binomial.disp()
(in dispmod)
は擬似尤度 (quasi-likelihood)
最大化でパラメーター推定やってる,
とのこと.
マニュアルよく読むと,
たしかにそう書いてある.
ベータ二項分布に合致するように
variance をややこしく決めて,
これを擬似尤度法で解いているらしい.
ふーむ.
-
しかもまぬけなことに,
今年 8 月末の生態学会釧路大会のときに,
私は粕谷さんからこの
dispmod
のことを教えてもらっていた
……
らしいんだけど,
まるっきり失念していた.
嗚呼.
-
ともあれ,
このあたりのベータ二項分布問題について,
粕谷さんがネット上に何か文書を掲載される予定,
だとか.
-
蛇足ながら,
quasi likelihood は擬似尤度なる訳語が定着しつつあるようだけど,
むしろもっと直訳的に「準尤度」とでもしたほうがよいかも.
理由として一番わかりやすいのは,
pseudo likelihood なるものがまた別にあり,
これも擬似尤度と呼ばれることあるからだ
(ニセもの好きな私としては「にせ尤度」と呼んでいるけど).
じつは pseudo likelihood と呼ばれるものには少なくとも二種類あり,
空間統計学でつかわれるものと,
(私は実際に使われているのを見たことないんだが)
未知の確率分布の平均と分散を定式化して
これを正規分布で計算してしまう方式
(……だったような?)
があって,
ですね.
-
dispmod
ついでに
……
ガンマ混合ポアソン分布を計算する
glm.poisson.disp()
関数のほうは,
昨日かいたとーり,
「ほぼ」負の二項分布モデルと考えてよいようだ
(何か iterative な方法で最尤推定やってると書いてある).
たとえば,
example(glm.poisson.disp)
で
> mod.disp
Call: glm(formula = incid ~ offset(log(pop)) + Age + Cohort, family = poisson(log),
weights = disp.weights)
Coefficients:
(Intercept) Age55-59 Age60-64 Age65-69 Age70-74
-8.645 0.823 1.549 2.128 2.696
Age75-79 Age80-84 Cohort1860-64 Cohort1865-69 Cohort1870-74
3.172 3.474 0.355 0.519 0.774
Cohort1875-79 Cohort1880-84 Cohort1885-89 Cohort1890-94 Cohort1895-99
1.012 1.151 1.299 1.546 1.575
Cohort1900-04 Cohort1905-09 Cohort1910-14 Cohort1915-19
1.628 1.464 1.372 1.256
Degrees of Freedom: 48 Total (i.e. Null); 30 Residual
Null Deviance: 9140
Residual Deviance: 30 AIC: 194
こういう結果でてくるんだけど,
同じデータセットを負の二項分布な一般化線形モデル計算関数
glm.nb() (in MASS pacakge)
で推定させると,
> glm.nb(formula = incid ~ offset(log(pop)) + Age + Cohort)
Call: glm.nb(formula = incid ~ offset(log(pop)) + Age + Cohort, init.theta = 479.389611087294,
link = log)
Coefficients:
(Intercept) Age55-59 Age60-64 Age65-69 Age70-74
-8.642 0.822 1.549 2.128 2.695
Age75-79 Age80-84 Cohort1860-64 Cohort1865-69 Cohort1870-74
3.166 3.472 0.357 0.520 0.775
Cohort1875-79 Cohort1880-84 Cohort1885-89 Cohort1890-94 Cohort1895-99
1.012 1.151 1.301 1.541 1.572
Cohort1900-04 Cohort1905-09 Cohort1910-14 Cohort1915-19
1.623 1.464 1.373 1.253
Degrees of Freedom: 48 Total (i.e. Null); 30 Residual
Null Deviance: 12400
Residual Deviance: 43.7 AIC: 535
……
となる.
推定値がびみょーに違うのは収束計算のやりかたが異なるので,
そのへんが反映されてるのではないか.
-
ただし,
上の計算結果をみると,
deviance とか AIC の値なんかは違うよね.
憶測だけど,
これは
glm.poisson.disp()
ではガンマ分布の部分は連続関数のまま計算してるのが
影響してんのではなかろーか,
と
……
いや,
ちょっとこれは変かな?
きちんと数値積分してれば両者は (だいたい) 一致するはず.
glm.poisson.disp()
で使っているという
Breslow (1984) の計算アルゴリズムとやらを調べんとわからんのかも.
-
急速に空腹になったので撤退準備.
どうも長距離を走ると,
あとになって急に空腹感をおぼえたりするよーな.
本日もぎょーむ進捗せず.
2015 研究室発.
2025 帰宅.
-
いかん.
夜も怠業状態つづく.
-
[今日の運動]
-
北大構内走 1430-1530.
ストレッチング.
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
-
[今日の食卓]
- 朝 (0930):
米麦 0.7 合.
キャベツ・ダイコン・豆腐・サバぶしの味噌汁.
- 昼 (1230):
蕎麦.
- 晩 (2200):
スパゲッティー.
タマネギ・マイタケのトマトソース.
2004 年 12 月 05 日 (日)
-
0900 起床.
あ,
また雪がたくさんつもってる.
朝飯.
コーヒー.
-
どうしてこう怠業状態が継続するのかねぇ
……
-
とりあえず包丁でも研ぐか
……
しかし仕事すすまず.
-
統計解析こんさるメイル書き.
またいろいろと教えていただき,
plot(g, which = n)
(g は glm オブジェクト,
n ∈ c(1:4))
すると q-q plot などができる.
しかし glm オブジェクトの q-q plot
はあまり役にたたん.
-
部屋の中が寒いと怠業につながるような気もする.
低体温症?
どうも寒さに鈍感な気がする.
ためしに暖房でもつけてみるか.
外はあいかわらずの降雪.
-
室温上昇したので,
とりあえず研究室に行ってみる準備には着手できた.
1620 自宅発.
湿雪.
かなり積もってる.
地下鉄北 12 条駅横の
ICI 石井スポーツで靴紐だの防水スプレイだの購入.
1029 円.
とはいえ,
これはしばらくはゴム長で歩いたほうがよいかも.
1640 研究室着.
-
粕谷さんからまたベータ二項分布について教えていただく
……
どうもこのややこしそうな確率分布は,
何やら壷モデル (urn model) で簡単に説明できるそうで.
ふーむ,
また何か
一般化超幾何分布
がらみの予感.
くわしくはまた後日,
ということで楽しみです.
-
で,
また統計学勉強.
しかしここ数日の勉強内容にあまり脈絡がない.
他人が見たら正気を疑うだろうなあ.
MCMC,
ニューラルネットワーク,
EM アルゴリズム,
変分ベイズ法などなど.
-
本日最後はまったくここまでとは関係なく
(そしてやるべき仕事ともまったく関係なく),
群集生態学や植生学で使われてる多変量解析技法の勉強.
The Ordination Web Page
とか
Jari Oksanen
(R の
vegan
package 作者)
のペイジとか面白い.
よく用いられている
DCA なる手法はめまいがするほど統計学的にはヘン,
というのがわかってしまった
……
よくもまぁ,
こんなやりかたを思いつくもんだ.
これにしろ,
あるいは先日の年輪気候学の「標準化」手法にしろ,
1970 年代 (計算機力がすごく限定されてた時代)
に開発された苦しまぎれなデータ解析技法を
いつまでも無批判に使ってんじゃないよ
……
-
なんつーか,
袋小路な進化のことを
「ガラパゴス諸島だ」
とけなすのが一部で流行してるよーですが
……
生物学関係の一部はまさに統計学的手法のがらぱごすと化しているようで.
関与してるヒト以外の誰にもその手法の正当性が理解できん状態.
-
しかし何よりおそろしいのは,
他ならぬ自分自身が新しいがらぱごす諸島を作りかねん,
という可能性で
……
-
ああ,
今日もぎょーむはススまなかった.
2200 研究室発.
ますます積雪がつづく
(最終的にこの 40cm の積雪になったそうだ).
2220 帰宅.
体重 74.0kg.
なぜ急に重くなる.
晩飯.
-
[今日の運動]
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
-
[今日の食卓]
- 朝 (0920):
米麦 0.8 合.
タマネギ・マイタケのトマトソース.
- 昼 (1300):
米麦 0.8 合.
ニラ・エノキダケ・豆腐・卵の炒めもの.
- 晩 (2330):
米麦 1.0 合.
タマネギ・マイタケのトマトソース.
はんぺん.
2004 年 12 月 06 日 (月)
-
0800 起床.
朝飯.
コーヒー.
0920 自宅発.
曇.
北区といえど,
さすが札幌市中央部.
除雪はススんでいる
(このあたり地環研まわりでどんどん新築されてる高層マンションに
入居者需要をみこんでいる理由かもしれない).
札幌市は今年度の除雪予算としてぢつに
153 億円
計上してる.
そして除雪車輌による除雪は車道・歩道をそれぞれ
一航過すればいいんだろうけど,
たいへんな労力だ.
0930 研究室着.
-
地環研まわりでは構内の雪倒木の片づけ作業が.
憶測するに,
9 月の
台風 18 号
で痛めつけられた樹木が,
土日にたくさん降った重い雪に負けてコケてるんではなかろうか
……
とすると苫小牧の調査地なんかでも,
と思って調べてみると,
むこうでは
雪が降ってない
ようで.
-
いつまでも怠業ばかりしてるわけにもいかんので,
アカマツ作図作業にとりくむ.
-
作業つまづく.
今回は R
で日本語文字いり作図をやらねばならんのだけど
……
{xy}lab や legend()
は問題ない.
しかし
expression()
や
mtext()
はダメなんだよね.
うう.
-
いろいろ試行錯誤しただけで昼飯前の仕事は終了.
昼飯.
-
PlotNet なるあやしげプロジェクトのあやしげ予算消化のための
予算計上調査につきあう.
かなりまぬけな状況.
-
1400 気をとりなおして作図作業再開.
R で完結するのはあきらめて LaTeX 併用わざに切りかえる.
-
ひとつめの図はできたが,
ふたつめは perl + gnuplot 作図時代のものだな
……
弱気になって EPS 出力をお茶部屋 iMac の Illustrator
でいじってみる.
-
やはりこういう手動なごまかしは通用せんわけで
……
釧路大会雑用でさんざん苦労したはずなのに,
重要なことをすっかり忘れていた.
EPS ファイルってのは,
Linux → Mac には渡せても,
Mac → Linux には不可能 (日本語文字が含まれる場合は)
ってのを忘れてた.
阿呆だ.
-
気合いいっぱつ perl + gnuplot 作図システムを少し改造する
……
10 分で終了.
最初からこうすればよかった.
しかしフォントまわりに不安は残る.
-
途中で別の雑用したり,
お茶部屋で怠業したり
……
1640 ひとまず終了.
無意味に時間かけてしまった.
不調だ.
-
お茶部屋雑談.
小川群落保護林
が阿武隈山地の一部とゆーのを始めて知った.
また統計学勉強,
など.
-
2030 研究室発.
2040 帰宅.
体重 74.2kg.
晩飯.
-
2316 また地震
(
震度分布).
このへんは震度 3 ぐらい.
-
[今日の運動]
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
-
[今日の食卓]
- 朝 (0830):
米麦 0.7 合.
ハクサイ・チカの味噌汁.
チカ
なる小魚が 20 匹 80 円ぐらいで売ってたんで買ったんだけど,
これってワカサギのたぐいなのか.
- 昼 (1310):
研究室お茶部屋.
米麦 0.8 合.
ニラ・エノキダケ・豆腐・卵の炒めもの.
- 晩 (2130):
米麦 1.0 合.
ハクサイ・チカの味噌汁.
はんぺん.
2004 年 12 月 07 日 (火)
-
0820 起床.
朝飯.
コーヒー.
0920 自宅発.
雨.
なんで,
雨なんだ.
0930 研究室着.
-
とある受験希望者 (外国人)
のため入試関連情報のメイルを送る
……
しかし地環研入試関連の更新はいまだに滞ったままだな.
こんなのでだいじょうぶなのかね.
-
さて,
次のぎょーむだが
……
様子がわからんので,
苫小牧直径モデルの説明の appendix 化作業にでも
取り組んでみるか.
ぼちぼちと.
われながらのんびりしすぎ,
という気もするが.
-
昼飯.
すでに先週の土曜日 (12/4) に,
雪野さんは子供を無事出産,
との朗報に接する.
めでたいめでたい.
-
昼飯後も appendix のつづき.
-
ちょっと R で遊んでみたり.
-
講座セミナーの予習.
今日のは難解そうだ.
-
1500 より
講座セミナー
,
本日は M2 立花さんで,
北海道内の
ミミコウモリ
のたぐいの遺伝的多様性 (アロザイム解析).
やはり難解なものであった
……
というのも,
このテのハナシでは
集団にでてくるパターンを説明するモデルが明示的でないためだ
(あえて言えば,
各分集団は無限集団と仮定,
というような).
集団間の遺伝子組成類似度みたいな量 (共分散みたいな量) ということになる
genetic distance
で系統樹らしきものを描いても,
これはわかりやすいものではない.
……
「集団間の相違はこのように生じる」
を表現する素朴な集団遺伝学モデルと対応がつかないためだ.
-
系統樹といっても「進化速度」とかとは関係ないので,
樹状図 (デンドログラム) というか,
ともかく平均距離法だろうが最近接結合法だろうが,
「枝の長さ」
が何を表現してんのかよくわからんし
……
いや,
まあ,
私自身があれこれすごく不勉強なのは認めますけど.
-
ということで,
セミナー後も集団遺伝学なヒトたちと議論.
-
1850 研究室発.
1900 帰宅.
体重 74.4kg.
いよいよ重い.
晩飯.
-
うーむ
……
粕谷さん出題の統計学難問になやむ.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0840):
米麦 0.7 合.
タマネギ・エノキダケ・豆腐・しらたきの煮物.
- 昼 (1300):
研究室お茶部屋.
米麦 0.7 合.
タマネギ・エノキダケ・豆腐・しらたきの煮物.
- 晩 (2030):
米麦 1.0 合.
ハクサイ・タマネギ・エノキダケ・豆腐・しらたきの煮物.
2004 年 12 月 08 日 (水)
-
0840 起床.
朝飯.
コーヒー.
朝からまた粕谷さん宿題を考える.
うーむ.
回答の腹案ができたので
0950 自宅発.
晴.
1000 研究室着.
-
で,
数時間かかって宿題の回答を試みる.
こういう内容.
いま読んでみると,
「相撃ち検定」
なる名前はあまり実体をうまく表現できていないな.
単純モデルが普通の検定では棄却できない,そして複雑モデルから得られる標
本では単純モデルのあてはまりを説明できないので,複雑モデルは棄却する,
というような「相撃ち検定」とでもいうようなアイデアですね.
たしかに面白いです……しかし,同時にこのような素直なアイデアは「検定」
の長い歴史のうえになんどもあらわれてはそのたびに却下されてきたのでは
(それゆえにモデル選択などが考案されて使われている),という予断というか
偏見もあります.
かかる予断はあるのですが,「相撃ち検定」はよろしくないでしょうという明
解な説明は思いつけない状況です (何か簡単な説明があるようには思うのです
が).とりあえず,「相撃ち検定」がうまくいかない事例は考えたので,それ
を説明してます.
パラメーターセット theta で定義される何かの連続分布 f(x | theta) を単
純モデル M0 とします.x はたとえばプラスマイナス無限大の範囲にあるとし
ます.M0 から得られた標本を {X} とします.ここでなんらかの推定方法で
{X} から複雑モデル M1 が得られるとします.この M1 は f(x | theta) の
「両端」を切断して規格化した切断分布で f(x | theta, min{X}, max{X}) と
いうように標本 {X} の最小値・最大値を「よけいなパラメーター」として含
む複雑モデルです.
これは「相撃ち検定」がうまくいかない可能性を含む事例です.まず,M0 か
ら生成される標本 {X'} を M1 にあてはめる「順方向」検定を検討します.こ
のときに,min{X} <= X' <= max{X} となる確率 (つまり M1 の下限・上限か
らはみださない確率) を q とします.この q が大きいほど M0 を棄却するの
は難しくなります.
いちばん極端には,f(x | theta) が一様分布 (うう,きしょく悪い) だとす
ると,有意水準 1 - q の検定で M0 は棄却できません.
単純モデル M0 が棄却できなかった場合には,つぎに「逆方向」検定をするこ
とになります.複雑モデル M1 から生成された標本 {Y} を M0 にあてはめて
みます.この標本 {Y} は,いわば M0 である確率分布 f(x | theta) から得
られる標本から「両端」を取り除いた (つまり尤度が高くないところを削除し
た) もので,M0 に対するあてはまりが {X} 以上である確率 r も小さくあり
ません.このときに,有意水準 1 - r の「逆方向」検定で M1 は棄却できま
せん.
極端例である一様分布の事例ですと,M1 から生成された {X''} を M0 にあて
はめると常に同じ尤度になります.これはもとデータ {X} から得られた尤度
に等しい値になります.つまり M1 は有意水準 0% で棄却できません.
つまり,「相撃ち検定」では,もとデータ {X} は M0 から生成されたにもか
かわらず,M0 も棄却できなければ M1 も棄却できない可能性があります.
切断分布などというといびつな事例のようですが,おそらく上のようなもどか
しい状況は,もし複雑モデル推定においていわゆる location parameter はう
まく推定しているのに scale parameter (ばらつき) のほうを実際より過小推
定するならば,いつでも発生しうる状況だろう,と思います.
上の「うまくいかなそうな事例」はとりあえずの思いつきなので,間違ってい
るかもしれません.当方でも再検討してみます.
あるいは粕谷さんの構想としては,M0 が棄却できないかつ M1 が棄却できる
ときだけ,この「相撃ち検定」が正当化されていればそれで十分,ということ
なのかもしれませんが……
しかしながら,
なんとも正気ならざる反例を考えつくもんだな.
あとで粕谷さんに指摘していただいて,
ようやく気づいたんだけど,
ここで述べようとしているのは,
どんなに標本数を増やしても M0 が棄却できず M1 も棄却できない
場合がありうる,
ということ.
上の「検定」で標本がどーのこーのと言ってるけど,
(これまた粕谷さんに教えていただいた)
parametric bootstrap な尤度比較検定を念頭においている
(しかし尤度評価のやりかたは何であってもさしつかえない).
つまり M0 から生成した乱数セットで M1 の尤度を評価したり
(「順方向」 --- これがふつうの parametric bootstrap 法),
あるいは M1 で生成された乱数で M0 で M0 の尤度を評価する
(「逆方向」 --- これが粕谷さんによる拡張),
といったものだ.
かなりばてきってしまった.
霜月さん
からアロザイム解析な系統樹に関して,
いろいろと教えていただく.
たいへん勉強になる.
Nested Clade Analysis
とか面白そうだなぁ
(検索するといろいろ出てくる).
しかし,
これは DNA のハプロタイプ樹とかがわかってないと使えないような
……
少なくともアロザイムに適用しようとするとかなり手直しが必要みたいな.
などとまた仕事とは直接関係ないところばかり勉強してみたり.
なんというかですね,
12 月であるにもかかわらず,
現時点で修論したうけがないのでとても気楽な状況なんですよ
……
うん?
なんか忘れてるような気も
……
よゆーありそうだから,
というわけでもないが,
ひどく観念論的な論文原稿の査読ひきうける.
たまには,
こういうのも読んで耐性をつけないとね.
研究費残金 30 万円.
今年はやけに消費してるじゃないか?
先月はじめの
鹿児島往還
が「豪遊」すぎたのかしらん?
粕谷さんから上記宿題回答についていくつかコメントいただく.
しかし本論はこれから,
のようで
……
赤坂君にまた別の
R
教材ペイジおしえてもらう.
札幌学院大の
Jin さん
(中国出身のかたのようで)
によるもので,
いちばん基礎的なところから
nnet()
によるニューラルネットワーク計算まで網羅している.
えー,
これとはまた関係なく,
R
調査.
本日はかなり錯乱しているな.
先日インストールした
Jari Oksanen
の
vegan
package の挙動調査.
これは
CANOCO
なる内容非公開な有料ソフトウェアの独占体制に
一石を投じるものになるかも.
Oksanen が準備した「線形多変量解析のアヤしさ」
デモンストレイションをいろいろひねくってみる.
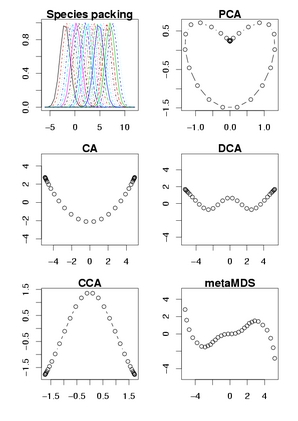
[species → score]
左上にあるように,
ある一次元の環境傾度にそって「等間隔」に植物種が分布している,
という状況
(架空群落).
調査地はこの軸上に一定間隔でならんでいる.
とうぜん解析結果は「植生は一次元の軸で説明できる」
というものになってほしい.
しかしながら
……
PCA は horse shoe 効果が極端にでて二次元上の
♥ 型になり,
CA は arch 効果でひんまがり,
DCA はそれを無理やりまっすぐにするときの恣意的な操作のせいで
ぐねぐねとまがってしまい,
CCA は環境軸を考慮してるのにやはり arch 効果がでてしまい,
arch 効果がないということになってる nonmetric MDS
でもなんだか奇妙なカタチに.
-
いかん,
苫小牧直径モデル appendix とか,
アカマツとかやるべきことをやらないまま一日が終ってしまった.
2020 研究室発.
2030 帰宅.
体重 73.8kg.
運動.
晩飯.
-
で,
なんだかこれまた当面の仕事とは関係ない遺伝学方面の
勉強に没頭してしまって,
ですね.
ひどく無軌道かつ逸脱しているような.
-
[今日の運動]
-
エアロバイク 40 分間.
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
-
[今日の食卓]
- 朝 (0850):
ヨーグルト.
不調ぎみなんで.
- 昼 (1430):
リンゴ.
- 晩 (2200):
米麦 1.0 合.
キャベツ・ダイコン・ブナシメジ・コンニャク・煮干の味噌汁.
2004 年 12 月 09 日 (木)
-
0830 起床.
不調.
生活周期がヘンだ.
朝飯.
コーヒー.
なんか「一日の中で,
アタマから正気でない考えがでる確率は朝がもっとも高い」
という奇妙な思い込みにとりつかれていて,
何かよいアイデアが出そうになるとそれに没頭する,
ということがあってですね
……
1000 自宅発.
晴.
1010 研究室着.
-
なにやらあやしげな書類に拘束されたり.
-
てなことその他あれこれで昼飯前が終ってしまうって,
どういうこと?
われながら,
ひどい.
いや,
そういった雑用するふりをして統計学本とか読んだり,
論文をダウンロードしたりとわき道にそれてしまって,
ますます雑用処理効率を落してしまったのは認めますけど.
昼飯.
-
しかし勉強してアタマをひっかきまわすことで,
新しいアイデアも得られる.
新しいアイデアは役にたたないことが多いんだけど,
アタマは新しいものが好きなので興奮状態になる.
そういうふうに,
これから数時間もアタマの中に居座られてはイヤなので,
ここに記録してアタマの中からは削除したい.
-
またしても集団遺伝学なハナシなんだが
……
ある遺伝子座 X (複数でも良いけどとりあえず単数)
でいくつかの中立なる対立遺伝子があるとする.
それぞれの局所的個体群から得られた有限個の遺伝子 X
の対立遺伝子の個数セットのことを,
遺伝子 X の組成の標本とよぶことにする.
とうぜんながら,
この標本 S が得られる母集団について,
われわれは多くのことを知らない.
-
母集団は確率分布 (N 個の対立遺伝子あるなら N 項分布)
によって近似的に表現されるとする.
すると,
われわれは組成の標本 S が得られる確率つまり尤度 L を計算できる.
-
では,
この母集団なる確率分布 F をどのように構成すればよいか?
ここで局所的個体群はひとつではなく複数あるものとしよう.
局所的個体群間の距離その他が「近い」と遺伝子 X の組成が似ている,
とする.
もしこれが成立するならば,
ある局所的個体群の母集団 F を他の局所的個体群の「合成」によって
構築できるかもしれない.
もちろん「合成」は単純な平均などではなく,
局所的個体群間の距離その他に依存して加重を変える加重平均となる
(この場合は標本を加重平均して合成する).
-
つまり母集団たる確率分布 F が「よその局所的個体群」の標本
・局所的個体群間の「距離」・その他に依存する関数として書いてしまい,
そこから標本 S が得られる尤度 L を最大化するように
未知パラメーター (距離依存性とか)
あれこれを推定してしまえばよい,
というだけのハナシ
(むろん他の局所的個体群についても同様に尤度を計算して,
全体の尤度を最大化する
……
といういつものやり口が今回に関してもホントに良いのかしらん?).
-
問題点は局所的個体群のサイズの効果とかを考えてないところだろうなぁ.
つまりこれでは大個体群 → 小個体群への流れ込みはありがちなのに
逆方向にはなかなか流れない
(正確に言うと,流れたことを検知するのが難しい),
といった当たりまえの現象をうまく表現できていない.
可能な解決策としては
……
困ったときのべいぢあん,
か?
それから「局所的個体群」とか言ってるけど,
これは単に標本あつめをやった場所にすぎない.
調査しなかった場所にも大個体群とかあるかもしれない.
そんなときはどしたらいいの?
-
上の問題一覧をまとめて解決する策のひとつとしては
……
これがいいのかどうかわからんが,
各局所的個体群の「個体群サイズもどき」みたいなパラメーターを仮定して,
それをモデルに組み込んで一緒に推定することだな
(これをランダム効果とすると形式的には経験ベイズモデルと同等になる).
未発見の局所的大個体群はその近くにいる誰かが「代行」してくれるはず,
と.
このアイデアでいくと,
ある場所での局所的個体群の組成の確率分布 F を推定するときに,
他の個体群だけでなくその場所自体も含めるべきかもしれん
……
あ,
それをやると「いっさいよそから影響ナシ」
という推定結果が得られるだろうな.
いやいや,
自分への影響つよければよそにも影響強い,
という効果があれば,
「自分への影響」 vs 「よそに及ぼす影響」
がうまく相殺されるかも
……
しかし標本数の多いところは,
それだけで大集団と見積もられる確率が高くなるな.
これはある意味,
実際にそうなっている可能性たかいわけだが.
-
この方法がどれぐらい正確かを validation するためには,
マルコフ連鎖モンテカルロ (MCMC) 法を援用せんといかんのかもね.
少なくともモンテカルロ法は必要だ.
-
……
というふうに,
逸般的な概要と問題点を列挙すればアタマ内から削除できそーなかんぢですね.
ぎょーむ日誌の重要な機能のひとつなんですよ.
欠点は「つみおろし」作業に時間かかること.
-
いつまでも遊んでばかりはいられないので,
苫小牧モデル appendix 書き作業にもどろうとする.
-
というところで,
粕谷さんから例のベータ二項分布モデルのファイルをいただく.
ふーむ
……
このあたりまた後日.
-
M1 牛原さんの輪読会予習につきあう.
例によってへなちょこな概念モデルが,
院生をわずらわせるわけだが
……
たしかにこの Chapter 10 はちょっと説明が不親切かも.
-
その問題章にでてくるモデルをだいたい解明して終了.
私にとっても予習になった.
腹へった.
2120 研究室発.
2130 帰宅.
体重 73.8kg.
晩飯.
-
[今日の素読]
-
Lehitilä, K. 2001.
Impact of herbivore tolerance and resistance
on plant life histories.
in
Life History Evolution in Plants
(Timo Olavi Vuorisalo and Pia Kristina Mutikainen eds).
Kluwer Academic Publishers.
-
[今日の運動]
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
-
[今日の食卓]
- 朝 (0900):
米麦 0.5 合.
キャベツ・ダイコン・ブナシメジ・コンニャク・煮干の味噌汁.
- 昼 (1350):
研究室お茶部屋.
米麦 0.7 合.
キャベツ・ダイコン・ブナシメジ・コンニャク・煮干の味噌汁.
- 晩 (2230):
米麦 1.0 合.
キャベツ・ダイコン・ブナシメジ・コンニャク・煮干の味噌汁.
2004 年 12 月 10 日 (金)
-
0830 起床.
ねむい.
朝飯.
コーヒー.
0930 自宅発.
曇.
0940 研究室着.
-
1000
Life History Evolution in Plants
輪読会.
本日の担当は M1 牛原さんで Chapter 10
食害に対する tolerance (災害復旧能力というか)
のハナシ.
また概念モデルがいろいろでてくるが,
すでに昨日「予習」したところなので,
ぢりぢりと進捗する.
というか,
まわりの院生たちも徐々に
「ひどく単純化された数式モデル」
の作図,
といったことに慣れてきたかんぢだ.
-
1240 ごろ終了.
ThinkPad X31 がまたまた電源まわりの不調で死んだ.
しばらく放置しておくことに.
同じ IBM 社製とは思えぬほど頑健なる ThinkPad 240Z
を代替機として準備する.
といっても,
例によってバックアップと
rsync
するだけで作業終了なんだが.
-
昼飯.
甲山さんが北アルプス雪山登りをやってたころのハナシうかがう.
なんでもある年の 3 月に
鹿島槍北壁
に登った帰りに
天狗尾根
を下っていたところ,
一人で滑落して
カクネ里
(これは北壁基部の谷底平坦部の通称で,
人間などは住んでいない)
まで落っこちてしまってそこでビバークしてから
登りかえした,
とか.
すごすぎる.
-
壊れ ThinkPad X31,
息をふきかえした.
本体の電源まわりがおかしいのか,
それとも AC アダプターがヘンなのか?
いままで前者ばかりをうたがっていたのだけど,
後者もちょっとおかしいことに気づいた.
なんか,
妙な電子音が聞こえるんだよね.
-
いろいろなメイル書きに時間がかかってしまった
……
-
そしてアヤしげきわまりない PlotNet 予算消化計画立案.
雪野さん計画にそうカタチで数値を操作するだけなんだが
……
ともかく,
環境省がらみはむちゃくちゃかつ,
ここの会計監査は硬直しつつあるので,
なかなかたいへんだ.
1920 研究室発.
1930 帰宅.
体重 74.0kg.
運動.
晩飯.
-
[今日の運動]
-
エアロバイク 45 分間.
-
腹筋運動 30 ×
3 回.
腕立ふせ 5 ×
3 回.
-
[今日の食卓]
- 朝 (0850):
米麦 0.5 合.
キャベツ・ダイコン・ブナシメジ・コンニャク・煮干の味噌汁.
- 昼 (1320):
研究室お茶部屋.
米麦 0.7 合.
キャベツ・ダイコン・ブナシメジ・コンニャク・煮干の味噌汁.
- 晩 (2200):
蕎麦.
キャベツ・エノキダケ・さつまあげの煮物.