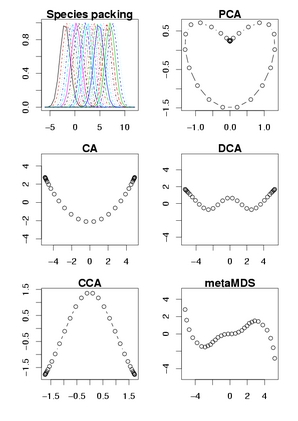
[species → score]
左上にあるように,
ある一次元の環境傾度にそって「等間隔」に植物種が分布している,
という状況
(架空群落).
調査地はこの軸上に一定間隔でならんでいる.
とうぜん解析結果は「植生は一次元の軸で説明できる」
というものになってほしい.
しかしながら
……
PCA は horse shoe 効果が極端にでて二次元上の
♥ 型になり,
CA は arch 効果でひんまがり,
DCA はそれを無理やりまっすぐにするときの恣意的な操作のせいで
ぐねぐねとまがってしまい,
CCA は環境軸を考慮してるのにやはり arch 効果がでてしまい,
arch 効果がないということになってる nonmetric MDS
でもなんだか奇妙なカタチに.