MCMCpack
調査にとりくむ.
これも一種の怠業に他ならない.
glms.R).
推定結果などは
これ
(glm.txt).

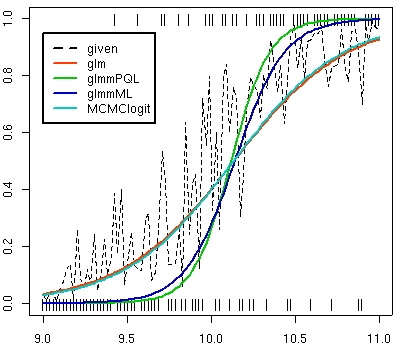
glm()
と
MCMClogit()
の推定結果が良かった場合).
一番単純な一般化線形モデル
glm()
と
一番複雑な MCMC ベイズ推定の
MCMClogit()
の結果がだいたいいっしょで
(glm(..., family = quasibinomial)
は推定値に関しては
glm()
と常にまったく同じ),
罰則つき擬似尤度法
glmmPQL()
は「傾き」のキツすぎる推定結果をだし,
最尤法による一般化線形混合モデル推定
glmmML()
はそこまではキツくない結果になる.
glmmPQL()
だけが異なる
glmmML()
はそもそも収束計算をしくじることが多く,
もっとも不安定な推定計算方法と言える.
MCMClogit()
の結果はよろしくないような.
何度やっても,
こういったばらつきをまったく考慮しない
glm()
とほとんど同じ推定結果になるんで,
これだったらベイズ推定とかやる御利益とか
何もないぢゃん.
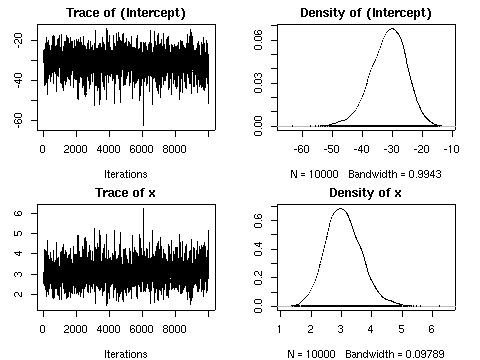
MCMClogit()
の出した事後分布.
この事例ではたまたま推定値の平均はそれっぽい値になっているけれど,
いっぽうで
variance がむちゃくちゃでかいんですけど
……
glm.binomial.disp()
(in dispmod)
は擬似尤度 (quasi-likelihood)
最大化でパラメーター推定やってる,
とのこと.
マニュアルよく読むと,
たしかにそう書いてある.
ベータ二項分布に合致するように
variance をややこしく決めて,
これを擬似尤度法で解いているらしい.
ふーむ.
dispmod
ついでに
……
ガンマ混合ポアソン分布を計算する
glm.poisson.disp()
関数のほうは,
昨日かいたとーり,
「ほぼ」負の二項分布モデルと考えてよいようだ
(何か iterative な方法で最尤推定やってると書いてある).
たとえば,
example(glm.poisson.disp)
で
> mod.disp
Call: glm(formula = incid ~ offset(log(pop)) + Age + Cohort, family = poisson(log),
weights = disp.weights)
Coefficients:
(Intercept) Age55-59 Age60-64 Age65-69 Age70-74
-8.645 0.823 1.549 2.128 2.696
Age75-79 Age80-84 Cohort1860-64 Cohort1865-69 Cohort1870-74
3.172 3.474 0.355 0.519 0.774
Cohort1875-79 Cohort1880-84 Cohort1885-89 Cohort1890-94 Cohort1895-99
1.012 1.151 1.299 1.546 1.575
Cohort1900-04 Cohort1905-09 Cohort1910-14 Cohort1915-19
1.628 1.464 1.372 1.256
Degrees of Freedom: 48 Total (i.e. Null); 30 Residual
Null Deviance: 9140
Residual Deviance: 30 AIC: 194
こういう結果でてくるんだけど,
同じデータセットを負の二項分布な一般化線形モデル計算関数
glm.nb() (in MASS pacakge)
で推定させると,
> glm.nb(formula = incid ~ offset(log(pop)) + Age + Cohort)
Call: glm.nb(formula = incid ~ offset(log(pop)) + Age + Cohort, init.theta = 479.389611087294,
link = log)
Coefficients:
(Intercept) Age55-59 Age60-64 Age65-69 Age70-74
-8.642 0.822 1.549 2.128 2.695
Age75-79 Age80-84 Cohort1860-64 Cohort1865-69 Cohort1870-74
3.166 3.472 0.357 0.520 0.775
Cohort1875-79 Cohort1880-84 Cohort1885-89 Cohort1890-94 Cohort1895-99
1.012 1.151 1.301 1.541 1.572
Cohort1900-04 Cohort1905-09 Cohort1910-14 Cohort1915-19
1.623 1.464 1.373 1.253
Degrees of Freedom: 48 Total (i.e. Null); 30 Residual
Null Deviance: 12400
Residual Deviance: 43.7 AIC: 535
……
となる.
推定値がびみょーに違うのは収束計算のやりかたが異なるので,
そのへんが反映されてるのではないか.
glm.poisson.disp()
ではガンマ分布の部分は連続関数のまま計算してるのが
影響してんのではなかろーか,
と
……
いや,
ちょっとこれは変かな?
きちんと数値積分してれば両者は (だいたい) 一致するはず.
glm.poisson.disp()
で使っているという
Breslow (1984) の計算アルゴリズムとやらを調べんとわからんのかも.