
[いきなりヘンな配置にしてみたり]
おいつめられた人間にありがちな逃避行動です.
あとで,
右のディスプレイの下敷きとして
岩波「生物学辞典」を使っている点に関して,
来室された宮崎さんからご批判を頂戴いたしました
……
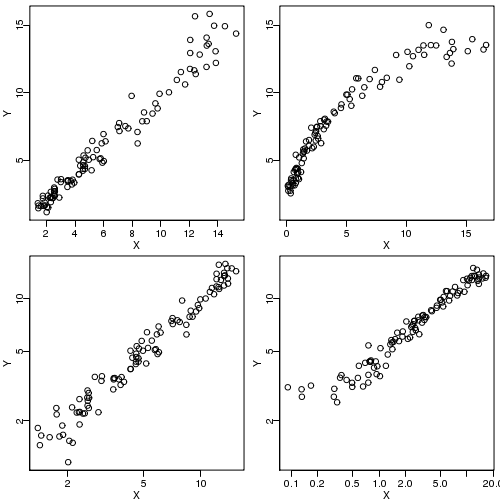
cor(x, y, ...)
なる関数があり,
ふつーは x, y は vector にするモンなんだけど,
これを行列にしてしまうと何だかヘンになります,
か
……
これをやると,各行列の列のくみあわせすべてで相関係数を計算します.
「これで正しいかどうかよくわからない」「結果がどうもおかしい」と思った
ら,以下のように簡単な例を自分で作って,自分の命じた演算がどのようなも
のであったのか,実験によって把握してください.
> (A <- matrix(rnorm(9), 3, 3))
[,1] [,2] [,3]
[1,] 0.33353 1.81914 -0.089742
[2,] -1.16268 -0.19822 2.300776
[3,] 0.14182 1.67105 -1.063475
> (B <- matrix(rnorm(6), 3, 2))
[,1] [,2]
[1,] -0.68314 -1.830202
[2,] 0.37239 -0.067488
[3,] -0.14917 1.186322
> cor(A, B, method = "kendall")
[,1] [,2]
[1,] -1.00000 -0.33333
[2,] -1.00000 -0.33333
[3,] 0.33333 -0.33333



im-change + $HOME/.profile
書きかえで
Anthy + scim
に戻した.




hosho.ees.hokudai.ac.jp
だけが単独で壊れてしまったようだ.
うーむ.
木曜日の夜か金曜日の朝まで
放置するしかないなぁ.
/var/log/messages:
... Mar 15 08:31:52 hosho kernel: lowmem_reserve[]: 0 0 0 0 Mar 15 08:31:52 hosho kernel: DMA: 3*4kB 0*8kB 1*16kB 1*32kB 0*64kB 0*128kB 1*256kB 1*512kB 0*1024kB 0*2048kB 0*4096kB = 828kB Mar 15 08:31:52 hosho kernel: DMA32: empty Mar 15 08:31:52 hosho kernel: Normal: 121*4kB 5*8kB 1*16kB 0*32kB 0*64kB 2*128kB 1*256kB 0*512kB 1*1024kB 0*2048kB 0*4096kB = 2 076kB Mar 15 08:31:52 hosho kernel: HighMem: empty Mar 15 08:31:52 hosho kernel: Swap cache: add 834267, delete 834204, find 10296703/10385219, race 3+611 Mar 15 08:31:52 hosho kernel: Free swap = 0kB Mar 15 08:31:52 hosho kernel: Total swap = 248996kB Mar 15 08:31:52 hosho kernel: Free swap: 0kB ...そもそもこの貧弱なる web server 機, こんなヘンなメモリ容量だったかな? メモリがこわれたかな?
[hosho:kubo]$ free -m
合計 使用済 空き領域 共有領域 バッファ キャッシュ
メモリ: 177 132 44 0 15 41
-/+ バッファ/キャッシュ:
76 100
スワップ: 243 18 224


library(RODBC)
使うか
glm()
したときの「水準間の差」の解釈について.
私の苦手な multiple comparison 系の問題だが
……
とりあえずこのように例題を生成してみる.
v.levels <- c("A", "B", "C")
d <- data.frame(
x = factor(rep(v.levels, 100), levels = v.levels)
)
d$y <- rnorm(nrow(d), as.numeric(d$x), 0.5)
fit1 <- summary(glm(y ~ x, data = d))
d2$x <- factor(d2$x, levels = c("C", "A", "B"))
fit2 <- summary(glm(y ~ x, data = d2))
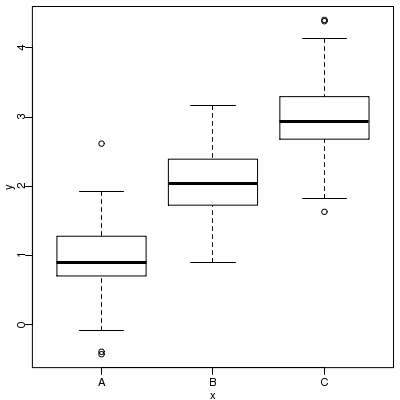
glm(y ~ x, data = d)
するとこうなる.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.93825 0.049526 18.945 5.0048e-53
xB 1.10903 0.070040 15.834 2.2999e-41
xC 2.06157 0.070040 29.434 4.7266e-90
次に水準をこんなふうに変更してみて,
d2 <- d
d2$x < - factor(d2$x, levels = c("C", "A", "B"))
単純に glm(y ~ x, data = d2)
するとこうなる.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.99982 0.049526 60.570 3.4240e-169
xA -2.06157 0.070040 -29.434 4.7266e-90
xB -0.95254 0.070040 -13.600 4.4517e-33
Estimate
の解釈は単純で,
水準をどう並びかえようが
本質的には同等の結果になる.
上記 Estimate
の組み合わせ & 足し算すればわかることだ.
Std. Error
の解釈なんだよね.
これは単純に「確率変数の和 (差) の分散」
を計算しても一致しないんだよね
……
glm(y ~ x - 1, data = d)
と「Intercept なし」モデルを評価してみる.
Coefficients: Estimate Std. Error t value Pr(>|t|) xA 0.9382 0.0495 18.9 <2e-16 xB 2.0473 0.0495 41.3 <2e-16 xC 2.9998 0.0495 60.6 <2e-16…… ふーむ, 0.0495. これは
sqrt(2 * 0.0495^2)
で 0.070004 となる数だよね.
つまり「Intercept あり」モデルの x[ABC]
の Std. Error
(0.07004)
に近い数字だなぁ.
このあたりを整理すると何かうまい説明ができそうな気が
……

