glm()
したときの「水準間の差」の解釈について.
私の苦手な multiple comparison 系の問題だが
……
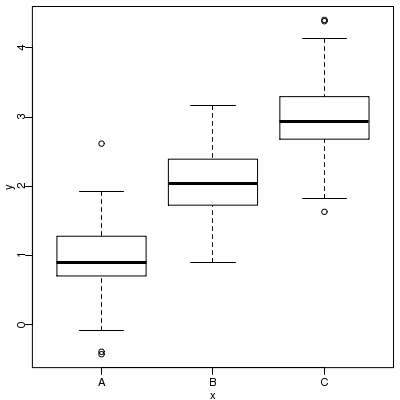
とりあえずこのように例題を生成してみる.
v.levels <- c("A", "B", "C")
d <- data.frame(
x = factor(rep(v.levels, 100), levels = v.levels)
)
d$y <- rnorm(nrow(d), as.numeric(d$x), 0.5)
fit1 <- summary(glm(y ~ x, data = d))
d2$x <- factor(d2$x, levels = c("C", "A", "B"))
fit2 <- summary(glm(y ~ x, data = d2))

glm(y ~ x, data = d)
するとこうなる.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.93825 0.049526 18.945 5.0048e-53
xB 1.10903 0.070040 15.834 2.2999e-41
xC 2.06157 0.070040 29.434 4.7266e-90
次に水準をこんなふうに変更してみて,
d2 <- d
d2$x < - factor(d2$x, levels = c("C", "A", "B"))
単純に glm(y ~ x, data = d2)
するとこうなる.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.99982 0.049526 60.570 3.4240e-169
xA -2.06157 0.070040 -29.434 4.7266e-90
xB -0.95254 0.070040 -13.600 4.4517e-33
Estimate
の解釈は単純で,
水準をどう並びかえようが
本質的には同等の結果になる.
上記 Estimate
の組み合わせ & 足し算すればわかることだ.
Std. Error
の解釈なんだよね.
これは単純に「確率変数の和 (差) の分散」
を計算しても一致しないんだよね
……
glm(y ~ x - 1, data = d)
と「Intercept なし」モデルを評価してみる.
Coefficients: Estimate Std. Error t value Pr(>|t|) xA 0.9382 0.0495 18.9 <2e-16 xB 2.0473 0.0495 41.3 <2e-16 xC 2.9998 0.0495 60.6 <2e-16…… ふーむ, 0.0495. これは
sqrt(2 * 0.0495^2)
で 0.070004 となる数だよね.
つまり「Intercept あり」モデルの x[ABC]
の Std. Error
(0.07004)
に近い数字だなぁ.
このあたりを整理すると何かうまい説明ができそうな気が
……
