optim()
の使いかたとか完全に忘れてて,
50 分も費やしてしまった
……
次にまた同じような問題にすばやく対処できるよーに,
ここに記録しておきますか.
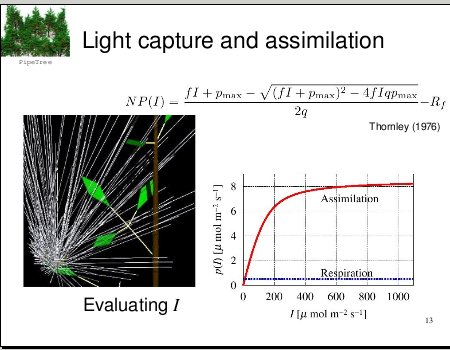
p.rate <-function(L, q)
{
tmp1 <- q[1] * L + q[2]
tmp2 <- tmp1^2 - 4 * q[1] * q[2] * q[3] * L
tmp2 <- ifelse(tmp2 < 0, tmp1^2, tmp2)
(tmp1 - sqrt(tmp2)) * 0.5 / q[3] - q[4]
}
# q[1]: f
# q[2]: p-max
# q[3]: q
# q[4]: R
square.err <- function(log.q, x, y)
{
v <- y - p.rate(x, exp(log.q))
v %*% v
}
estimate.parameters <- function(x, y)
{
fit <- optim(
par = c(log(1), log(10), log(0.0001), log(2)),
fn = square.err,
method = "Nelder-Mead",
x = x,
y = y
)
exp(fit$par)
}
fit <- estimate.parameters(d$light, d$p.rate)
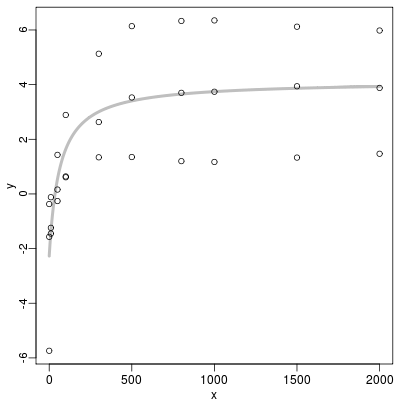
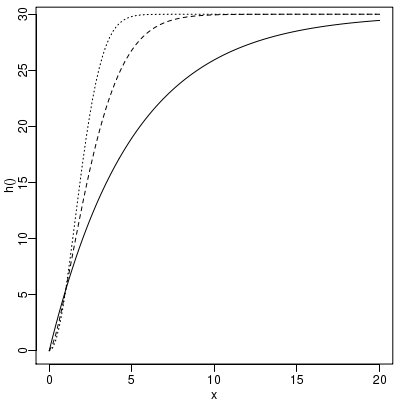
plot(d$light, d$p.rate)
xx <- min(d$light):max(d$light)
lines(xx, p.rate(xx, fit))
ちょっとめんどうなのは,
このイヤらしい光-光合成曲線モデルのパラメーターども,
どれも常に正であるようにするところで
……
上の R コードにあるとおり,
optim()
内では log 変換したパラメーター世界で Nelder-Mead な
試行錯誤ふらふらを実施している.