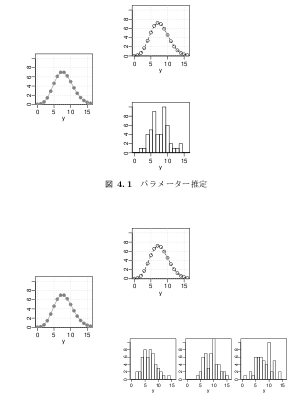
[LaTeX 依存な……]
図の部品は R の library(Cairo)
で PDF ファイルとして生成するんだけど,
そこから先のコマかい作業は
LaTeX の picture 環境でケリをつける方向に
ナガされている
……
R 作図わざ本
役者としては library(grid)
を駆使すべきなんだろうけど
……
うーん,
フォントまわりのめんどうから逃避してるのかな.
左の図はまだ配置などを検討してるだけです.

library(Cairo)
で PDF ファイルとして生成するんだけど,
そこから先のコマかい作業は
LaTeX の picture 環境でケリをつける方向に
ナガされている
……
R 作図わざ本
役者としては library(grid)
を駆使すべきなんだろうけど
……
うーん,
フォントまわりのめんどうから逃避してるのかな.
左の図はまだ配置などを検討してるだけです.
sudo apt-get install vim-latexsuite
してみた.
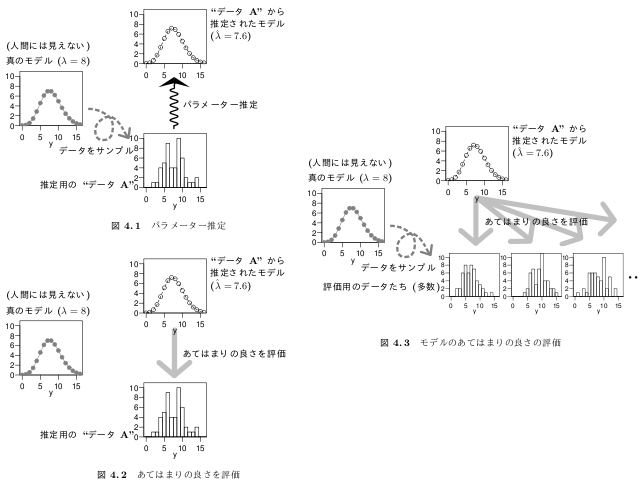
\newcommand
な tempalte 機能) と
R と inkscape
で生成してみた.
ぐねぐね矢印は,
inkscape 波線
わざ (つまり関数プロットわざ).


exp(b1)
exp(b1 + b2 * x)
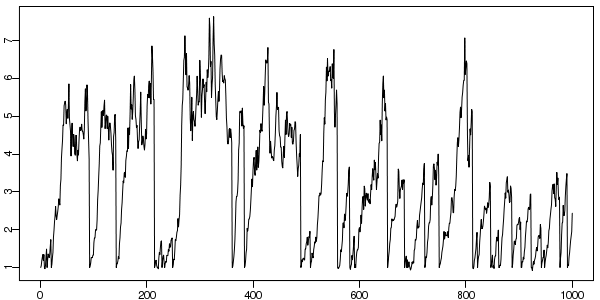
x なる説明変数は,
まったく何の意味もない単なる乱数
> summary(m.fit[4,] - m.fit[5,])
Min. 1st Qu. Median Mean 3rd Qu. Max.
-3.57e+00 -7.09e-01 -2.48e-01 -4.82e-01 -5.07e-02 -6.13e-06
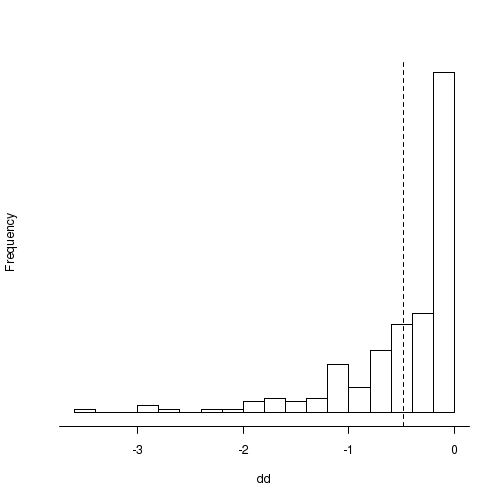
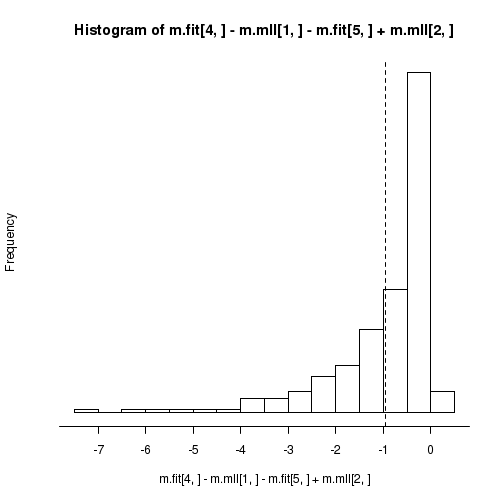
> summary(m.fit[4,] - m.mll[1,] - m.fit[5,] + m.mll[2,])
Min. 1st Qu. Median Mean 3rd Qu. Max.
-7.05000 -1.38000 -0.50100 -0.94800 -0.11500 0.00339
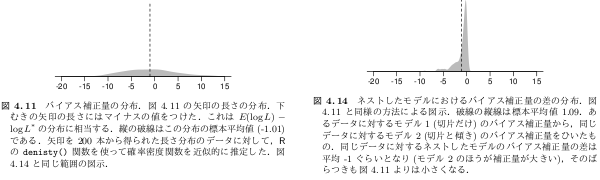
値の範囲がゼロより大きくなっているけど,
これは正しい.
> summary(m.mll[1,] - m.mll[2,]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.0088 0.0533 0.2560 0.4670 0.6650 3.4800
> pchisq(1:2, 1) [1] 0.68269 0.84270



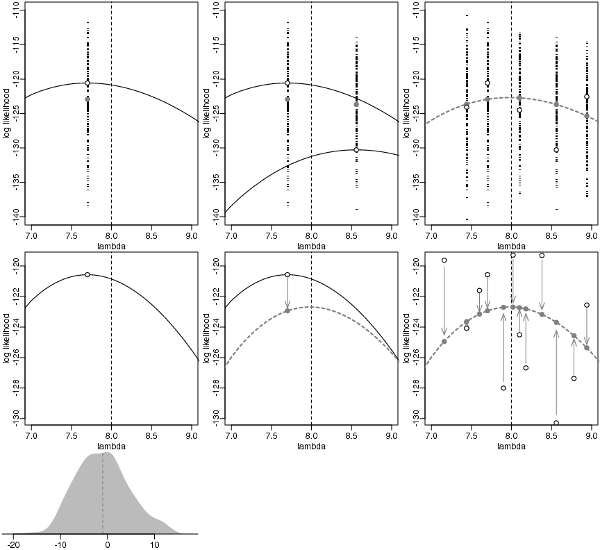
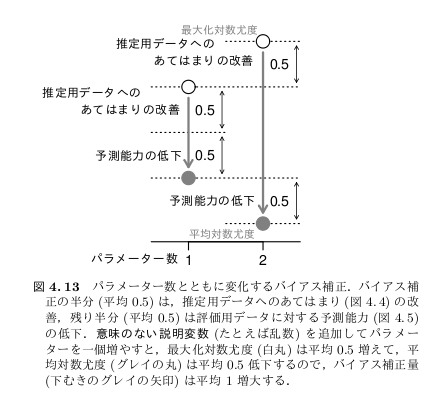
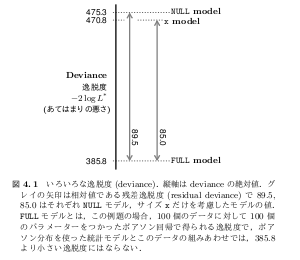
「真のパラメータ」と「推定したパラメータ」 および 「現在ある有限のデータ」と「将来の無限のデータ」で 2X2=4 とおりの組み合わせがある.そのうち1と2の差から1/2, 3と4の差から1/2が期待値として得られ,2と3の差の期待値はゼロ. 問題の揺らぎの項は2と3の差.
で・・ 問題は1,2,3,4がそれぞれ4つのどれかだが(笑) また間違えそうなので演習にする. ちなみに3本の放物線は1,2,3,4の関係を示したもの.で, この 1, 2, 3, 4 は
| 現在の有限個データ | 将来の無限個データ | |
|---|---|---|
| 推定したパラメーター | 1 | 4 |
| 真のパラメーター | 2 | 3 |
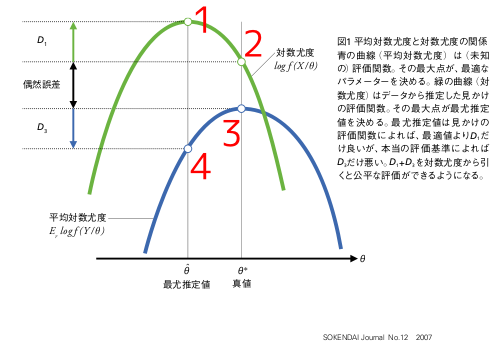
要は,「真のパラメータのモデルの無限データでの評価」と「推定したパラメータの(推定に使った)有限データでの評価」の差がほしいわけじゃないということだ.これでは半分しか出ない.この「差」とは, 上の北川図でいうと 1 - 3 のことで, 「偶然誤差」の期待値はゼロだから, D1 のことになる. 7/24 ぎょーむ日誌とかに図示してるよーに, 2 × D1 は (パラメーター数が 1 の場合) 自由度 1 のカイ二乗分布にしたがうので (という導出はもはやハヤリではないそうなのだが), D1 の平均は 0.5 となる.
必要なのは,「推定したパラメータのモデルの無限データでの評価」と「推定したパラメータの(推定に使った)有限データでの評価」の差.前者がほしいもの.後者が最大対数尤度. これで正しい値になる.これは上の北川図の赤数字でいうと 1 - 4 となる. 岩波統計モデル本の新第 4 章では, こんなかんぢで数値例を示す方針でやってます.
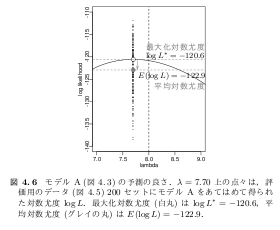
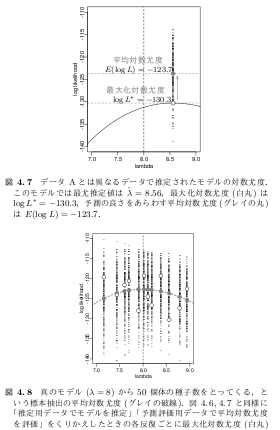
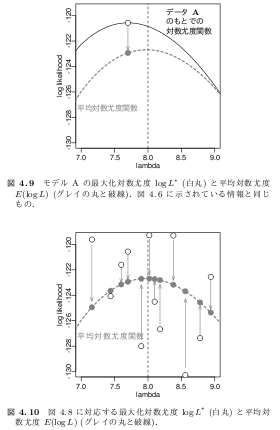

で・・ 問題は1,2,3,4がそれぞれ4つのどれかだが(笑) また間違えそうなので演習にする. ちなみに3本の放物線は1,2,3,4の関係を示したもの.あいかわらず「3 本の放物線」 のナゾがとけない. 距離の評価としては 1 - 2 (北川図の D1 = 平均 0.5), 2 - 3 (偶然誤差 = 平均 0) 3 - 4 (D2 = 平均 0.5) の三つがあるわけだが …… これらの距離は放物線の式ではない …… うーむ?
eigen()
で右固有ヴェクトルもとめて終了,
となるかもしれない.
これで成長速度のばらつきなんかも近似的ながら
きちんと反映させられる.

T
とか
F
といった名前のオブジェクト (vector とか data.frame とか)
はヤバいということ.
理由は R の中の真偽値である
TRUE
と
FALSE
それぞれの省略形が
T と F
だから.
T とか F
といったしょぼい真偽値は使わない」
と言われるかもしれないが
(私だって使わないけど),
問題は R の package なのだ.
R package の中には
T とか F
といった真偽値をつかっているものがあって
(例: library(R2WinBUGS)),
こいつらの動作はテキめんにおかしくなるんだよね.
TRUE
などは下のように「守られて」いるので,
> TRUE <- "abc" 以下にエラー TRUE <- "abc" : 代入の左辺が不正(do_set)です真偽値としてつねに問題なく使用可能.
