

「真のパラメータ」と「推定したパラメータ」 および 「現在ある有限のデータ」と「将来の無限のデータ」で 2X2=4 とおりの組み合わせがある.そのうち1と2の差から1/2, 3と4の差から1/2が期待値として得られ,2と3の差の期待値はゼロ. 問題の揺らぎの項は2と3の差.
で・・ 問題は1,2,3,4がそれぞれ4つのどれかだが(笑) また間違えそうなので演習にする. ちなみに3本の放物線は1,2,3,4の関係を示したもの.で, この 1, 2, 3, 4 は
| 現在の有限個データ | 将来の無限個データ | |
|---|---|---|
| 推定したパラメーター | 1 | 4 |
| 真のパラメーター | 2 | 3 |
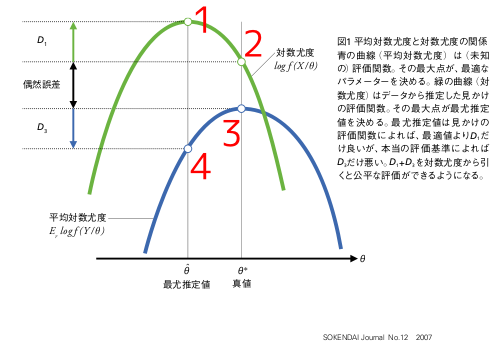
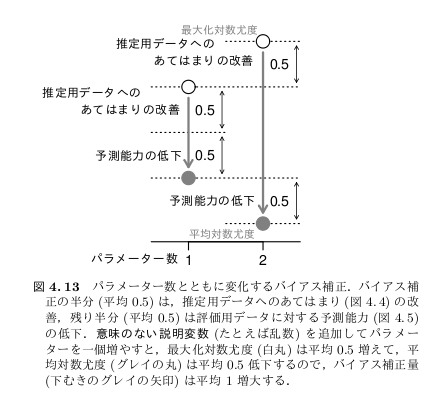
要は,「真のパラメータのモデルの無限データでの評価」と「推定したパラメータの(推定に使った)有限データでの評価」の差がほしいわけじゃないということだ.これでは半分しか出ない.この「差」とは, 上の北川図でいうと 1 - 3 のことで, 「偶然誤差」の期待値はゼロだから, D1 のことになる. 7/24 ぎょーむ日誌とかに図示してるよーに, 2 × D1 は (パラメーター数が 1 の場合) 自由度 1 のカイ二乗分布にしたがうので (という導出はもはやハヤリではないそうなのだが), D1 の平均は 0.5 となる.
必要なのは,「推定したパラメータのモデルの無限データでの評価」と「推定したパラメータの(推定に使った)有限データでの評価」の差.前者がほしいもの.後者が最大対数尤度. これで正しい値になる.これは上の北川図の赤数字でいうと 1 - 4 となる. 岩波統計モデル本の新第 4 章では, こんなかんぢで数値例を示す方針でやってます.
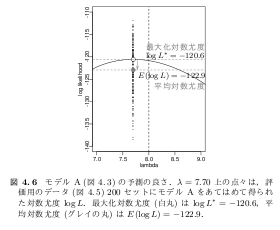
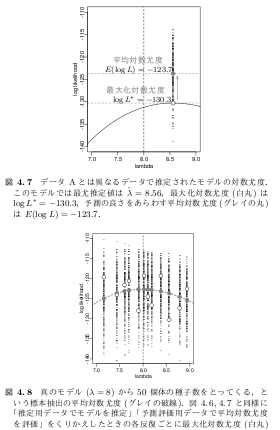
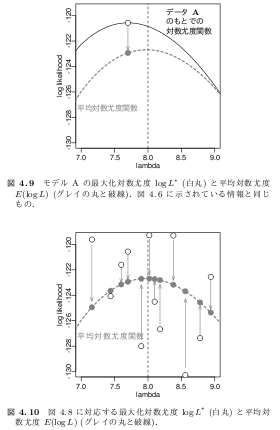
で・・ 問題は1,2,3,4がそれぞれ4つのどれかだが(笑) また間違えそうなので演習にする. ちなみに3本の放物線は1,2,3,4の関係を示したもの.あいかわらず「3 本の放物線」 のナゾがとけない. 距離の評価としては 1 - 2 (北川図の D1 = 平均 0.5), 2 - 3 (偶然誤差 = 平均 0) 3 - 4 (D2 = 平均 0.5) の三つがあるわけだが …… これらの距離は放物線の式ではない …… うーむ?