ぎょーむ日誌 2009-01-(21-31)

2009 年 01 月 21 日 (水)

• 0710 起床． 朝飯． コーヒー． 0900 自宅発． 晴． 電気代しはらう． 1636 円． 暖房はガスのみなので， 電気代は冬でもほとんど上昇しない． 0925 研究室着．
• なんだか朝の一時間ちょいをいきなり航空券手配に使ってしまった …… 生態学会盛岡大会 (3 月) 往復のものなんだけど． いつもはもっとてばやくすませてしまうんだけど， 予算がひっぱくしている， 行きは仙台・帰りはいわて花巻， といっためんどうが多少あってですね． つまりお金をケチろうと特割にしようとするんだけど， ちょうど 3/20 前後で特割ナシ期間が始まったり， 3/20 でとっとと帰ってやろうと思うんだけど， 費用の点を考えると 3/19 夜遅くに仙台から帰ったほうがトクか? いやいや盛岡-仙台の新幹線は高いから …… などなどといったどうでもよい検討に時間を失ってしまったわけですよ． とりあえず手配はすませたけど， まあなんともがっくしな朝に．
• 窓の外はまたいつのまにやら雪．
• もはややけくそで， ハンパに残っている雑用処理． しつこく研究室の備品調査， これは今週金曜日に会計係に廃棄処分を申請する必要あり． その他もろもろ．
• データ解析こんさるメイルかきも二件ほど． まあ， これは雑用ではなく本業ですな．
• 北大の研究者データベイスにあれこれ入力． このデータベイスはなかなかヒドいもので， さらに改悪されてるように思えるのだが …… 一番ひどいのはゐんどーづの IE 以外では挙動がおかしい， proxy error とか server side な JAVA がしくじってるかんじ． とにかくそういった抜本的なところもヒドければ， ユーザーインターフェイス側もひどくて， 大学などのお役所的まる投げ感横溢する …… とにかく外部のヒトの目にふれないところはいよいよヒドいのだ．
• なんとか片づけて昼飯． ふう．
• なぜかしら昼飯後も雑用処理 (データ解析こんさるメイル書きも) がつづいてしまう． 2/23 の統数研 公開講座 のお手伝い (とあるヒトに指摘されて驚いたのだが， 私は伊庭さんの「スタンド」かも，という説があるそーだ)， 謝金がでることになっているので 先方からこちらの事務室に委嘱状を送ってもらったりする必要がある， とわかったのでその連絡．
• ついでに 2/23 まわりの航空券・宿泊の手配． これはまあ旅費は先方もちだし， 東京一泊旅行なので迷う余地もナシ …… と思っていたのだが， 統数研周辺はあいかわらず宿がなく， いろいろ迷ってしまったのだが (とまた時間を浪費) けっきょく以前に泊まった最近傍宿 (これはなんとなく避けたかった) にすることに． うーむ．
• 雑用ばて． ふーむ， Perl 軽量フレイムワーク MENTA …… などと当面のぎょーむには関係ないことなど調べてしまった． うう．
• サル論文の自分のターンを終わらせようとする作業 …… 今日はあまりススまなかった． Discussion 節のおわりかたをもうちょっと改訂する必要がありそう． Introduction のハナシとかみあってない部分があるので．
• 1900 研究室発． 晩飯． 2020 帰宅．
• [今日の運動]
  • うんどう休養日になってしまった ……
• [今日の食卓]
  • 朝 (0810): 米麦 0.8 合． ホウレンソウ・ネギ・ブロッコリー・ブナシメジ・ホタテのトマトカレー．
  • 昼 (1340): 研究室お茶部屋． 米麦 0.8 合． ホウレンソウ・ネギ・ブロッコリー・ブナシメジ・ホタテのトマトカレー．
  • 晩 (1930): カレーつづきの日々 (明日もカレー) なので， 自宅ちかくの卯和で 時鮭 (ときしらず，と読むらしい) を焼いたものを食べた． おいしいなぁ．

2009 年 01 月 22 日 (木)

• 0800 起床． ねむい． また電燈つけっぱなしで寝てしまった …… うう． 朝飯． コーヒー． 0945 自宅発． 晴． 放射冷却その他で気温は低い． 1000 研究室着．
• ちょっとネット下ばたらきぎょーむ． 院生に指示されつつ， 来月末の 研究会 に「日帰り」のご案内追加， とか．
• ふーむ， Suzuki & Suzuki なるまにあっくな枝の論文がでてますな ……
• サル論文修正作業をおわらせたいのだが …… なにかしら圧迫感を感じたので， 宮田さんの論文修正にとりくむ．
• 昼飯後も作業つづく． 鍋嶋さんから総説 「樹高成長の制限とそのメカニズム」 の別刷を送っていただいた． ありがとうございます． ちょうどよいタイミングともうしますか， これは宮田さん論文とかなり関係があるので， 勉強しなくては．
• とりあえず最初の 10 ペイジぶんぐらいみたので (あいかわらず時間かかりますな)， 宮田さんをおよびして修正すべき点について いろいろ説明してみる．
• ひとまず終了したんだけど， すでに夕方．
• メイル書きなどしつつ， サル論文のほうにとりくんでみる．
• しかしあまりススまぬうちに撤退． 来週の月・水曜日の授業の準備ができてないのに， これはまずいなあ． 1850 研究室発． 1905 帰宅． 晩飯の準備． 晩飯．
• [今日の運動]
  • ふけんこうな日々がつづいてしまってイヤになるなぁ ……
• [今日の食卓]
  • 朝 (0800): シリアル． ヨーグルト．
  • 昼 (1220): 研究室お茶部屋． 米麦 0.8 合． ホウレンソウ・ネギ・ブロッコリー・ブナシメジ・ホタテのトマトカレー． リンゴ．
  • 晩 (2000): 米麦 0.8 合． ホウレンソウ・ネギ・ブロッコリー・ブナシメジ・ホタテのトマトカレー．

2009 年 01 月 23 日 (金)

• 0830 起床． 不調だ． 朝飯． コーヒー． 0950 自宅発． 南方から暖気が入ってきたので雨． 気温も高く， 札幌市の除雪費用削減に役たちそう (雪まつり準備のヒトたちには困った状況だけど)． しかし明日はまたすごい寒気がくるらしいんで， 札幌市内はアイススケートリンク状態になりそう． 1010 研究室着．
• また雑用で午前中が終わってしまった． 不調だ．
• いやはや， と昼飯． 外の天気もだんだん荒れてきた．
• テングザル論文修正作業のつづき …… ぢりぢりと進捗させて， 当方のターンを終了させた． ファイルダウロードできるように準備して， マレイシアに「とりあえずできました」 メイル送信．

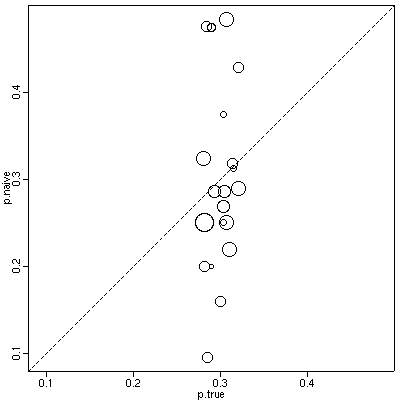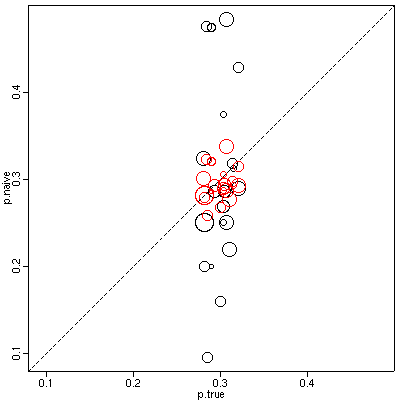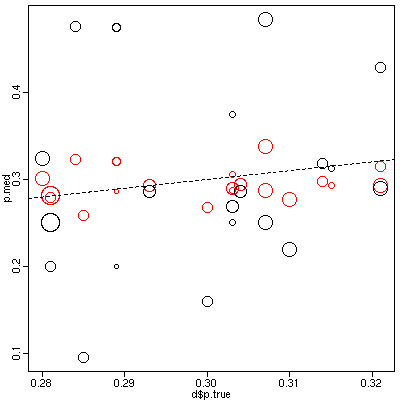
  Introduction なおしてみると，discussion 末尾あたりはまだ改訂が必要かな
  という気もしました．
  
  ・multi-level society (MLS) の構造と機能の定量的な定義は依然あいまいなまま
    (この論文では何も解決しない問題かもしれません)
  ・これと関連して MLS の何を理解したいのかがよくわからない．
    川べりにおける行動中の MLS 的な挙動 (ワニよけ川わたり, Yeager) は
    いかにも MLS 的な行動ですが，集団規模増大による捕食回避なら他の
    動物でもありそう．
  ・日中の森林内での MLS 的な行動……と末尾に書かれているが，森林内で
    band のようなものを形成している，と考えているのだろうか? 草原とは
    異なりそういうことはなさそう，というハナシだったと思います．
  
  このあたり，もうちょい整理してみる必要があるように思います．
  

  時刻はすでに 1630 近い． いやはや．
• ひとやすみ． 私の ThinkPad X31 上では A キーの横の Caps Lock キーを /usr/lib/kbd/keymaps/i386/qwerty/us_Ctrl_CAPS.kmap.gz で

  	keycode  29 = Caps_Lock
  	keycode  58 = Control
  

  というふうに Control と取りかえていたんだけど， 考えてみたら Caps Lock なんてジャマなだけ & 不要ぢゃん， と気づいたので

  	keycode  29 = Control
  	keycode  58 = Control
  

  と設定してみた． すこしすっきり．
• 来週の月・水曜日の 授業 の準備によーやくにしてとりくみはじめてみる ……
• しかしススまないので現実逃避． うーむこの LaTeX seminar な投影資料作りはヤメてしまって， ひょっとしたら OpenOffice.org の Impress (poorpoint みたいなやつ) だったらこの圧迫感のもとでも気軽に作業できるかも， といった錯覚にオチいってしまったので， Impress を起動してみる． しかし R とかで作った PDF ファイルを「画像ファイルとして読みこむ」 ができない …… まあ， そもそも PDF 読みこみができるソフトウェアは世の中にほとんどないわけですが (MacOS X の世界はベツとして) ……
• ひょっとしたら新ヴァージョン OpenOffice.org 3 ならできるかも， という方向に錯覚が悪化してしまったので， Linux 版の 3 の導入にとりくんでみる． すると日本語入力まわりその他でつまづいてしまった (これはおもに Linux 版で生じるとらぶるで， 他の OS 版ではこんなことにはならないだろう)．
  • (おそらく OpenOffice.org 2.4 を残しているため?) そもそも起動しない: libuno_sal.so.3 が見つかりません， といったエラーがでる． 解決策としては (おススめできないものだが) インストール package の RPMS ディレクトリ内で

    sudo rpm -Uvh --force openoffice.org-ure-1.4.0
    

    というふうに手動かつ強制的な操作をすると /opt/openoffice.org/basis3.0/ure-link/lib/ 以下に必要なライブラリがインストールされる．
  • 起動しても文字入力がいっさいできない: こちら を参考にして /opt/openoffice.org3/program/soffice 内を編集， SAL_NO_XINITTHREADS=true; export SAL_NO_XINITTHREADS という行の行頭コメントマーク (#) をはずす． すると Vine Linux 4.2 のもとでも文字入力できるようになる．
  • 環境変数 LANG=C のもとで起動した OpenOffice.org では， SCIM などをつかった日本語入力ができない: まあ， こんなヘンな設定をしているのは私ぐらいでしょうけど．
• さて， かんぢんの PDF ファイルの読みこみだが， OpenOffice.org3 になっても「できない」． しかしながら， 世の中うまくしたもんで， OpenOffice.org 拡張機能サイト で配布されてる Sun PDF Import Extension [Beta] を使うと PDF ファイルを読みこめるようになるみたいだ (beta 版だけど)． pdfimport.oxt なるファイルをダウンロードし， 起動した OpenOffice.org のツール → 拡張機能で「追加」 できる．

• で， やってみたんだけど， たしかに PDF 読みこめるんだが (正確にいうと，「画像ファイルとして読みこみ」 はできないんだけど， ファイルとして「開く」と OpenOffice.org Draw がこれを開いてくれる)， かならずしも正確には読まない． 上下の図で示されているようにタテ軸がびみょーにずれる． これは手動で補正する以外ない (OpenOffice.org オブジェクトに変換されているので 自由に操作できる)． それ以外はわりとうまく変換できているように思う (日本語文字とかどうなるかわからんけど)．

• なお上の図で q みたいなヘンなシンボルがあるけれど， これは OpenOffice.org がわの問題ではなく， おそらく当方の Vine Linux 4.2 ghostscript + IPA font 設定が 原因で生じている呪われ状態． xpdf とかで開くと当該テスト用 PDF ファイルはこんなかんぢなんだけどね．

• …… てな試行錯誤でオワってしまいましたよ． とほほ． 1940 研究室発． 2005 帰宅． 晩飯の準備． 晩飯．
• [今日の運動]
  • ふけんこうな日がつづく ……
• [今日の食卓]
  • 朝 (0910): 米麦 0.8 合． 卵焼． ヨーグルト．
  • 昼 (1330): 研究室お茶部屋． 米麦 0.8 合． レトルトパウチドカレー．
  • 晩 (2130): 米麦 0.8 合． ダイコン・豆イカの煮物．

2009 年 01 月 24 日 (土)

• 0850 起床． すごく寝てしまった． 朝飯． コーヒー． 洗濯． 怠業．
• 現状の整理をしてみますか …… 現時点で圧迫感の主因となってる げんこー・ぢゅぎょー系なあれこれ:
  • 1 月末授業 (1) 1/26 (月) GLM の基礎: これを 3 月の 自由集会 で使いまわせるような内容にしたい …… と思っていたのだが， もはや時間もないのでこういう一石二鳥は「まったくムリ」 だとわかった
  • 1 月末授業 (2) 1/28 (水) 階層ベイズモデルの基礎: これを 2 月の 統数研ベイズ講習会 で使いまわせるような内容にしたい …… と思っていたのだが， やはり M1 あいてに「たくさん教える」のは無理なので， 二回にわけて GLM だけを教えることにする
  • 2 月の 統数研ベイズ講習会: テキストを提出しなければならない (2/5 〆切) …… これを例の工学系学会誌のベイズ解説記事 (3/31 〆切) に使いまわせるようにしたいとは思っているんだけど， はてさてどうなることやら?
  • car.normal() 解説 記事の修正: 今月末まで?
  • 「蟻」解説記事原稿: とりあえずワクと図表は LaTeX 的に準備されて， あとは本文を書いていくばかりなのだが， しばらく中断が続きそうだ …… おそくとも 2 月中になんとかしないといけない
  • 「R の作図わざ」本のほんやく原稿: 共立出版の原稿チェックがぽちぽちと進行中なので， 当方も対応しなければならない …… なんとか日常ぎょーむ化したい
  • 岩波統計学本: 圧力もあることだし ぽちぽちと書きススめなくては …… 上の R 本作業がオワったあとに， なんとか日常ぎょーむ化したい
  したうけ系はしばらく進捗できない状況にある:
  • テングザル論文: 昨日自分のターンをとりあえず終了させた
  • 生態学会発表 & 論文かきにむけたウミガメモデル再計算: とうぶん，むり?
  • 苗場山の樹木のいる・いないデータのベイズ解析したうけ: とりあえず階層ベイズモデリング & MCMC 計算は終了した …… さっさと解説かいて納品しなくては ……
  • 帯広樹木開花モデリングの計算したうけ: とうぶん，むり?
  • 開花制御遺伝子発現時系列データの統計モデリング計算のしたうけ: とうぶん，むり?
  うーむ ……
• えーと， とにかくこれから処理すべき順番を考えると，
  1. 1/26, 1/28 の授業が終了するまで: 他のコトはススまない
  2. 2/5 の公開講座テキスト〆切まで: おそらく， この期間もまた他のコトはススまないでしょう …… いや， car.normal() 解説記事の修正版を生態学会編集部に送る必要あり
  3. 2/23 の公開講座まで: 10-12 日間ぐらいは「蟻」原稿かき (「脱」アリの最終段階) とか， R 作図わざ本， 下うけいくつかに時間を使えそう
  4. 3/17 の生態学会大会まで: 大会にむけて準備すべきことは ウミガメ ポスター発表の準備と GLM 自由集会 の準備， 「脱」ウミガメ (つまり最終的にはウミガメ論文投稿してウミガメから逃げる) をめざしてウミガメ方面をがんばるべきかも
  5. 大会終了以降: 今回は早めに盛岡から撤退するわけだが， 3 月末〆切の階層ベイズ解説 (というより紹介?) 記事を書かねば …… もし時間があればやはり盛岡前にどうにかすべきか?
  基本的にしんぐるたすくなのだが， いくつかのぎょーむは容赦なくわりこんでくる:
  • テングザル論文: あともうちょいで投稿できそう
  • 宮田さん論文: まだまだ
  • 大学院生の急患， とか
  R 作図わざ本ぎょーむなんかは 2-3 日に集中してやってしまうべきなのか …… それとも何とか「日常ぎょーむ」化すべきか?
• ちょっとうんどう． 昼飯 …… くってもなかなか大学に行こうという気にならない． ちょっとクタびれてますよ． ぎょーむボイコットしてますな．
• 蛇足ながら， この語原は Charles Boycott 大尉なる人名だそーで …… なになに， 皆で一致団結した場合のみボイコットとゆーのか? だったら， ぽいこっとでいいや …… いやいや， 私の 全細胞がぎょーむを拒否 しているから， やはりボイコットなのか?
• いやはや． 1500 自宅発． 曇． 今日は寒い． 何もかも凍結． 1520 研究室着．
• 研究室についてもボイコットだかぽいこっと状態が継続する．
• しかし授業の準備は誰も代行してくれないので， 説明に使う例題などまた作ってみる．
• 1940 研究室発． 2000 帰宅． 晩飯の準備． 晩飯．
• [今日の運動]
  • 腹筋運動 30 × 3 回． 背筋運動 30 × 3 回． 腕立ふせ 10 × 3 回． スクワット 100 回． ストレッチ．
• [今日の食卓]
  • 朝 (0940): 米麦 0.8 合． ハクサイ・油揚・すり身ダンゴのスープ． 鶏レバのショウガ煮．
  • 昼 (1330): 米麦 0.8 合． ハクサイ・油揚・すり身ダンゴのスープ． 鶏レバのショウガ煮．
  • 晩 (2100): 米麦 0.8 合． ハクサイ・油揚・すり身ダンゴのスープ． ヨーグルト．

2009 年 01 月 25 日 (日)

• 0855 起床． ずれた生活周期を修復するのは難しい． 体力的には回復しつつあるように思う． 朝飯． コーヒー． 洗濯． 少し怠業． 1100 自宅発． 晴． 気温 -3°C ぐらい． しかも次の寒冷前線が接近中． 買いもの． 1125 研究室着．
• 夜までぢゅぎょー準備つづく． けっきょく， 昨日試行錯誤してみたおうぷんおひすの使用はあきらめて， いつもどーり LaTeX seminar なシステムで． しかし昨日発見した PDF ファイル OpenOffice.org とりこみわざは役にたった ……
• 今回は「説明変数 X が重量などサイズであるときには， log(X) を使った線形予測子 & family = poisson(link = "log") とかで GLM ``アロメトリック'' わざを御伝授しましょう! …… などなどお買いドク感あふるる内容なのだが ……

• …… しかしながら， このような数式をちょっとでも使ってしまった説明ってのは ほとんどの M1 には理解されないものだ (現象 (データ) と数式のあいだに大きすぎる断絶がある)， とゆーのが近ごろの発見でもありますな …… まあ，わかるヒトもいることだろうし， べつに問題ないけど．
• 明日の授業は 1630 からだし， 未完成状態だけど本日は撤退しますか …… 1920 研究室発． 1940 帰宅． 晩飯の準備． 晩飯．
• [今日の運動]
  • 運動休養日になってしまった ……
• [今日の食卓]
  • 朝 (0940): 米麦 0.8 合． ハクサイ・油揚・すり身ダンゴのスープ． 鶏レバのショウガ煮．
  • 昼 (1330): 研究室． 米麦 0.8 合． トマト． リンゴ …… サンふじ (青森産 75 円)， なかなかうまい． 収穫されてからかなり時間たっていると思うんだけど， 保存がうまいのか味がおちてない．
  • 晩 (2100): 米麦 0.8 合． ハクサイ・油揚・すり身ダンゴのスープ． 鶏レバのショウガ煮． ヨーグルト．

2009 年 01 月 26 日 (月)

• 0710 起床． あまりよく眠れなかった． 寒い． 今朝の最低気温は -10°C ぐらいだったそーで． アルミサッシが氷結してるので窓があかない． 朝飯． コーヒー． 0905 自宅発． 晴． 0920 研究室着．
• ぢゅぎょー準備のつづき …… なんだかへろへろしてますなぁ ……
• ひとーとり準備おわった． 講義のーとくばるわけではないので， URL とか書いたチラシを一枚つくって 30 枚こぴー． 紙のムダかなぁ． ああ， 授業サイト から例題関係もダウンロードできるようにしなくては …… で， 終わってみたら時刻はすでに 1520． なんとものろくさい …… うう．
• マレイシアの松田君からテングザル写真などをまた送っていただく …… 今回は キナバタンガン 川ぞいのもの． キャプションによると: テングオス, ちょっと寂しそうなテングオス, テング♀とアカンボウ, クロコダイル (テングの天敵), オランウータン♀．

• しかし写真だけでなくサル論文も送られてきたので， 授業 30 分前まで修正作業しなければならなかった …… うー
• 1630 より C104 で 統計学授業． 参加者 30 名ちょっとあいてに GLM 入門編みたいなハナシを． やはり本日はへろへろぎみだったのか， 説明がいくつか脱落していた (GLM とは何の略かとか， ポアソン分布のくわしい説明とか) …… これはあとから投影資料を修正．
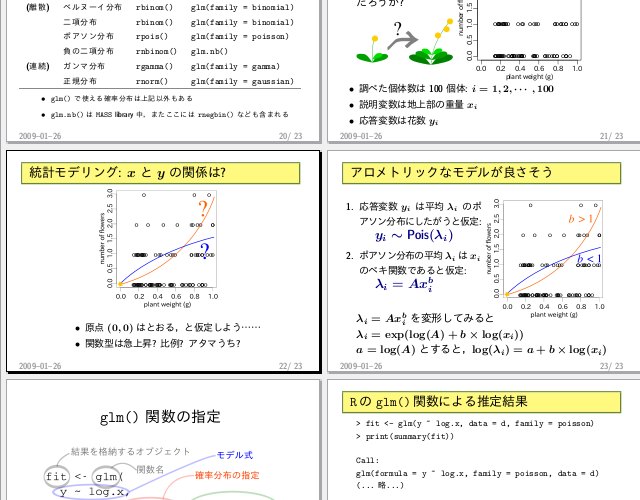
• 授業後の質問としては， glm() の family はどう選んだらよいか， という 1755 授業終了． あとは水曜日にもう一回やればいいだけだ ……
• 晩飯くってから 1900 フィールド科学センターで ベイズカエル本 輪読会． 本日は川森さん・宮田さん担当の第 5 章 Regression and correlation なのだが …… 著者のどくとくのセンスともうしますか， よくまあこんなヘンてこな統計モデリングを思いつくものだ， と感銘うける内容． かなり邪悪というか破戒的な． 善男善女はマネしないほうがよいでしょう．
• 2115 研究室発． 2130 帰宅．
• [今日の運動]
  • またまたうんどう休養日 ……
• [今日の食卓]
  • 朝 (0820): 米麦 0.6 合． ハクサイ・油揚・すり身ダンゴのスープ． 鶏レバのショウガ煮．
  • 昼 (1330): 研究室． 米麦 0.8 合． 鶏レバのショウガ煮．
  • 晩 (1820): 研究室． 米麦 0.8 合． 鶏レバのショウガ煮．

2009 年 01 月 27 日 (火)

• 0730 起床． ねむい． 朝飯． コーヒー． 0845 自宅発． 曇． 0900 研究室着．
• ネット雑用とか． A 棟とりこわしにあたってネットワーク環境をどう疎開させるか， とゆー問題． 以前は， 「あの」北大情報基盤センターに何かしらマトモな対応がひとつでもできるとは思えない， とゆー前提で疎開プランを考えていたのだけど， 他の A 棟さーばー管理者氏たちと相談してるうちに， まあ， 今のうちから時間をかけて交渉してみるか， と試みてみることになった．
• 1030 より井田君の D 論公聴会に出席． 100 周年記念会館． Keynote 使いたおしのイフェクト満載で圧倒する発表 …… とくに D な院生たちは「ここまで演出しなければならないのか」 といった圧力を感じてしまったようだ． 内容的には予備審ですでに聞いたものばかりであったが …… 質問時間があったのでサイズと重量分配の関係とか， 生活史の過程で変化する重量分配と phenological syndrome みたいなものって調べられてるのかしらん， とお尋ねしてみたのだけど， そういう研究はあまりないそーで． 理論的な予測みたいなのは以前からあるんだけど， 皆さんあまり興味が持てないところかな． たぶん予測ほど単純ではない結果が得られると思うのだが．
• 明日夕方のぢゅぎょー準備 ……
• 昼飯後も準備作業つづく．
• ロジスティック回帰に関しては前年のものを使いまわすことにしよう． いろいろ改訂・補足が必要になるけど．
• とりあえず logistic 回帰部分はできた …… 1850 研究室発． 買いもの． 1920 帰宅． 晩飯の準備． 晩飯．
• offset 項例題をひねくる． GLM 自由集会でも使いまわせそうなのが， なんとかできた …… ような気がする．
• [今日の運動]
  • またうんどう休養日になってしまった ……
• [今日の食卓]
  • 朝 (0810): 米麦 0.8 合． ハクサイ・ホッケすり身の味噌汁．
  • 昼 (1320): 研究室お茶部屋． 米麦 0.8 合． ハクサイ・ホッケすり身の味噌汁．
  • 晩 (2100): 米麦 0.8 合． ハクサイ・ホッケすり身の味噌汁． ヨーグルト．

2009 年 01 月 28 日 (水)

• 0825 起床． ふちょー． 朝飯． コーヒー． 1000 自宅発． 晴． 1015 研究室着．
• 夕方までひたすら授業の準備． 時間かかりすぎだよなぁ ……
• 1630 より本年度最後の北大 授業． 今日も 30 人ぐらい相手に， offset 項わざと logistic 回帰の説明． てーまは「脱」割算 …… しかし， ねむそーに聞いてた M1 のたいはんは割算値まみれな 修士論文を書くんでしょうなあ．
• 授業終了後， やや複雑なネット雑用． いわば住人のいない廃屋の裏口を蹴やぶって家宅進入するような ハナシで …… うーむ， GRUB の single user モード はちょっとひと手間かかる， とわかった (いまだに私のまわりは LILO 起動なんで)．
• 1910 研究室発． 1930 帰宅． 晩飯の準備． 晩飯．
• [今日の運動]
  • 不健康な日々がつづく ……
• [今日の食卓]
  • 朝 (0850): 米麦 0.6 合． ハクサイ・ホッケすり身の味噌汁．
  • 昼 (1230): 研究室． 米麦 0.8 合． キムチにぎり飯．
  • 晩 (2130): 米麦 0.8 合． キャベツ・ニンジン・ネギ・シイタケ・ソーセイジのレモン酒蒸し． キムチとワカメのあえもの． 茎ブロッコリーのゴマあえ． ヨーグルト．

2009 年 01 月 29 日 (木)

• 0810 起床． いまいちな日々がつづく． 朝飯． コーヒー． 0930 自宅発． 晴． 今日は気温が高い． しばらくするとまた真冬日がつづくようだ． 0945 研究室着．
• 志水さんから連絡いただき， 地衣類繁殖器管密度の 階層ベイズモデル解析 論文の accept 通知がよーやくとどきました (驚くべきことにメイルで!)， とのこと． めでたい． 地衣類 まにあ業界の有名ぢゃーなる に日本人ペア初登頂， というよくわからぬ記録達成? この研究は 2006 年 10 月ごろに JAGS や WinBUGS の戦力化ともうしますか， 研究に使えないかと試行錯誤していたわけだが， このデータ解析はゐんばぐす適用の第一号となった (2006-10-29 あたり)．
• 昨日とその前の ぢゅぎょー 投影資料の手直し作業． 基本事項のいくつかの説明がぼろぼろと脱落していたので 説明追加 …… われながらヒドいハナシだ． 両方とも修正してアップロード． 今回のふたつのファイルを統合・圧縮すれば， 3 月の GLM 自由集会 で使いまわせそう， という気分になってきた． 苦あれば楽あり， が実現するだろうか?

• 生態学会さーばー雑用．
• 来週金曜日に統数研公開講座の教材を提出しなければならないのだが …… その前に， 生態学会誌の car.normal() 解説記事を修正作業をするか． おっと 1300 から宮崎さんの D 論公聴会だった．
• で， 1300 から百周年記念会館で D 論公聴会を拝聴する． 苫小牧のハクウンボク・ササの研究は以前にうかがったことがあるのだけど， 奈良県ねたのスギについて聞くのは今回が初めて． 毎年繁殖するスギなんかでも前年の繁殖実績の影響をうける， ということで …… マスティング的なハクウンボクとのちがいはどのあたりだろう， と考えてしまった． 繁殖のコストなるものはありがちな考えかたなんだけど， 宮崎さんの発表で紹介されてたシュート間の同化物転流 (ハクウンボクは非繁殖シュートから繁殖シュートに動く) みたいなことが可能な樹木とそうではない樹木があって， といったハナシはないのかな．
• 研究室にもどって昼飯．
• で， まぬけなことに， 解説文改訂とかばーれたー書き， 原稿ファイルダウンロード準備とかで夜になってしまった． まあ， そのあいまにデータ解析こんさるとか， 用事メイルかきとかやったけど ……
• うーむ， とクビをひねりつつ， 1850 研究室発． なんとなくヨワりぎみなかんぢがしたので， 札幌駅のスターバックスによって， Tazo tea Zen (ティーバック 24 個 800 円) を買ってかえった． 1920 帰宅． 晩飯の準備． 晩飯．
• 現状の整理をしてみますか …… M1 あいての授業と car.normal() 解説改訂は終わった． 残された げんこー・ぢゅぎょー系なあれこれ:
  • 2 月の 統数研ベイズ講習会: テキストを提出しなければならない (2/5 〆切) …… これを例の工学系学会誌のベイズ解説記事 (3/31 〆切) に使いまわせるようにしたいとは思っているんだけど， はてさてどうなることやら?
  • 「蟻」解説記事原稿: とりあえずワクと図表は LaTeX 的に準備されて， あとは本文を書いていくばかりなのだが， しばらく中断が続きそうだ …… おそくとも 2 月中になんとかしないといけない
  • 「R の作図わざ」本のほんやく原稿: 共立出版の原稿チェックがぽちぽちと進行中なので， 当方も対応しなければならない …… なんとか日常ぎょーむ化したい
  • 岩波統計学本: 圧力もあることだし ぽちぽちと書きススめなくては …… 上の R 本作業がオワったあとに， なんとか日常ぎょーむ化したい
• したうけ系はしばらく進捗できない状況にある:
  • テングザル論文: 敵国語作文 editing 過程にほうりこまれている． このまま投稿してだいじょうぶなのか? とゆー気がしないでもないけど．
  • 生態学会発表 & 論文かきにむけたウミガメモデル再計算: とうぶん，むり?
  • 苗場山の樹木のいる・いないデータのベイズ解析したうけ: とりあえず階層ベイズモデリング & MCMC 計算は終了した …… さっさと解説かいて納品しなくては ……
  • 帯広樹木開花モデリングの計算したうけ: とうぶん，むり?
  • 開花制御遺伝子発現時系列データの統計モデリング計算のしたうけ: とうぶん，むり?
  うーむ ……
• えーと， とにかくこれから処理すべき順番を考えると，
  1. 2/5 の公開講座テキスト〆切まで: おそらく， この期間も他のコトはススまないでしょう ……
  2. 2/23 の公開講座まで: 10-12 日間ぐらいは「蟻」原稿かき (「脱」アリの最終段階) とか， R 作図わざ本， 下うけいくつかに時間を使えそう
  3. 3/17 の生態学会大会まで: 大会にむけて準備すべきことは ウミガメ ポスター発表の準備と GLM 自由集会 の準備 (これは M1 授業の投影資料を使いまわせそう)， 「脱」ウミガメ (つまり最終的にはウミガメ論文投稿してウミガメから逃げる) をめざしてウミガメ方面をがんばるべきかも
  4. 大会終了以降: 今回は早めに盛岡から撤退するわけだが， 3 月末〆切の階層ベイズ解説 (というより紹介?) 記事を書かねば …… もし時間があればやはり盛岡前にどうにかすべきか?
• [今日の運動]
  • あいかわらずふけんこうな日々 ……
• [今日の食卓]
  • 朝 (0850): 米麦 0.6 合． キャベツ・ニンジン・ネギ・シイタケ・ソーセイジのレモン酒蒸し．
  • 昼 (1410): 研究室お茶部屋． 米麦 0.6 合． キャベツ・ニンジン・ネギ・シイタケ・ソーセイジのレモン酒蒸し．
  • 晩 (2010): 米麦 0.6 合． キャベツ・ニンジン・ネギ・シイタケ・ソーセイジのレモン酒蒸し． ヨーグルト．

2009 年 01 月 30 日 (金)

• 0830 起床． 4 時ごろにいったん起きて， 2 時間ぐらい眠れなかったのだが， また寝てしまって起きたらこの時刻だった …… うーむ， 不調パターンがつづきますな． 朝飯． コーヒー． 0930 自宅発． 晴． 0945 研究室着．
• さっさと公開講座 (私の分担部分はいわば「ゐんばぐす Why & How」) の準備しなければならないのだが …… ぢゅぎょー準備ばかりでイヤになってしまったのか， たまには勉強しなくてはとかつぶやきつつ， 鍋嶋・石井解説文 「樹高成長の制限とそのメカニズム」 を勉強． これはよくまとまっていますな． そして樹高成長なるものは依然としてナゾばかり， というかんぢだ．
• 昼飯．
• …… いかん， イヤな雑用メイルかきに着手しなくては， と考えていたのだけど， なかなか着手できなくて (とうめんの仕事にも雑用にも関係しない) プログラミング言語の最新事情あれこれについて調べてしまった． アタマぼけぎみですな．
• とりあえず B 棟 1F のネットワーク室に現状を偵察にいく．

[ネットワーク室といっても]

こういう巨大な「スイッチ」(手前右) のハコが鎮座してるだけで ……

[動いてない server 機なんかが]

ぞろぞろあるだけ． じつは机の下の一台だけがまともに動いている．

[このへん片づければ]

A 棟の server 機器を疎開させることができるかも． なんだか北大内の地球環境のネットワークに関するはりがみがあったんだけど， A 棟と大計が光ケイブルで直結してるのか， 情報教育棟から B/C 棟と分岐しているのか， よくわからないかきかただった．

• とりあえず情報基盤センターに状況・実現したいこと・要望したいこと を最小限にまとめたメイルを送ってみる． どうなることやら． とにかく交渉あるのみ， だ．
• ついでにもう一件ネット雑用． 研究室の (あまり使われていない) 無線 LAN アンテナの調査 …… うーむ， とくに問題ないように思うけど．
• 統数研公開講座ねたというか架空な例題を考えてみる …… これが思いつかなくて， 準備がとどこおっているんだよね．
• 講義のーとにのってるやつは簡単すぎるような気がするし， かといって複雑な例題は教える側にとっては自滅的というほかないし ……
• そうそう， 昨日 car.normal() 解説文を改訂したんだけど， MCMC とは何かといった説明がわかりにくい， と指摘された． もともとは

  尤度が良くなる、 つまり観測データへのあてはまりが良くなるように パラメーターを変化させていくという目的は ベイズモデルの MCMC 法でも最尤推定法と同じである。 しかしながら、 MCMC 法では「尤度が良くなる方向」にばかり進むのではなく、 何か特定の値を探索するのではなく尤度が良いときの 「モデルの状態」にむしろ興味がある、 というところが異なっている。 この手法を適用することで、 ベイズ統計モデルで定義された事後分布そのものを直接に推定はできないが、 事後分布からの多数のランダムサンプルが得られる (以下、サンプリングとよぶ)。 これによってわれわれは事後分布の性質を知ることになる。

  といったかんぢで， MCMC 計算の中での パラメーターの値の 「動き」みたいなのに着目していたんだけど， たしかに上の説明は「何が何やら?」いまいちなかんぢだ． そこで以下のように改訂してみた．

  (MCMC 計算は) 最尤推定法と同じく尤度 (統計モデルの観測データへのあてはまり) にもとづくものである。 数値的な最尤推定法では試行錯誤によって 尤度最大となるパラメーターの値を推定する。 ベイズモデルの MCMC による推定でも パラメーターの値を試行錯誤で変化させる。 しかしながら、 MCMC 法ではこの試行錯誤 (以下、サンプリングとよぶ) で得られたパラメーターの値のセットが 事後分布からの無作為抽出標本となるような、 巧妙な「値の変化のさせかた」のルールが適用されている。 このようにしてサンプリングされた値のセットによって、 われわれはパラメーターの事後分布の性質 (事後平均値など) を推定できる。

  より抽象的な記述になっているわけだが， まあ中途半端に具体的な「動き」なんかを書くより， 「どういった値が得られるのか」 に焦点をあててみたわけだが …… どうでしょうかね?
• てなことを書いてたら， まさにこの 昨日提出した原稿ファイルに関して， めんどうな指示が …… この作業フェイズさえ終えてしまえば， ほぼすべて完了のはず， とがんばってみる．
• しかし最後までは到達せず撤退． 1920 研究室発． 買いもの． 1950 帰宅． 晩飯の準備． 晩飯．
• [今日の運動]
  • うー ……
• [今日の食卓]
  • 朝 (0900): 米麦 0.8 合． 鶏レバのショウガ煮． キムチ．
  • 昼 (1310): 研究室． 米麦 0.8 合． 鶏レバのショウガ煮． コーンスープ．
  • 晩 (2200): 米麦 0.8 合． ダイコン・ネギ・鶏肉のスープ． 鶏レバのショウガ煮． ヨーグルト． リンゴ．

2009 年 01 月 31 日 (土)

• 0800 起床． よくねた． 朝飯． コーヒー． 洗濯． 怠業．
• ちょっとうんどう． 昼飯． これでさっさと大学に行こうとしたのだが …… なぜかしら Planet Earth の DVD 再観賞に数時間を費してしまった． Planet Earth からよみとれる教訓: キツネは地球上のあちこちにあらわれる成功した哺乳類捕食者? まあ， ネコ・クマのたぐいも適応放散がんばってはいるけれど．
• 1630 自宅発． 曇． 1645 研究室着．
• うーん， 統数研 公開講座 であつかう例題， 生態学ねたはヤメにして 「野球の打者の打率」 とかどうかな?

[割算推定値のアヤしさ]

といって悪ければ， 難しさ． 横軸が「ホントの打率」なるアヤしい量で， タテ軸が 20 打者の 10-50 打数から安打数 / 打数 で推定された値． マルの大きさが打席数をあらわす． 「ホント」はすべての打者の打率は 0.3 ぐらいなんだけど， これぐらいの打数だと一割から五割打者までばらつく． とゆーことで， 規定打席 なるキマリがあるわけだが …… ま， それはともかく．

[階層ベイズモデルによる「補正」?]

赤マルは階層ベイズによって「補正」された打率． たいしたことないぢゃん， と思われるかもしれないが， 私からみるとけっこうウマく「補正」してるような気がする ……

[横軸を拡大表示]

ま， こんなかんぢでもっともらしく「補正」してるように見える …… 面白いのは「改悪」されてる点があることで， 割算推定値のほうが「ホント」の値に近かったのに， ベイズ推定では集団平均の方向に牽引されてしまっている ……

• どうもばててきたので (風邪ぎみか?)， 2010 研究室発． 2030 帰宅． 晩飯の準備． 晩飯．
• [今日の運動]
  • 腹筋運動 30 × 3 回． 背筋運動 30 × 3 回． 腕立ふせ 10 × 3 回． スクワット 100 回． ストレッチ．
• [今日の食卓]
  • 朝 (0830): 米麦 0.6 合． ダイコン・ネギ・鶏肉のスープ．
  • 昼 (1230): イソップベイカリーのクロワッサン．
  • 晩 (2120): 米麦 0.8 合． ダイコン・ネギ・鶏肉のスープ．