更新: 2018-01-16 12:26:08
生態学のデータ解析 - R で JAGS (rjags 編)
- R から JAGS を使う
library(rjags)について説明します- CRAN: http://cran.r-project.org/web/packages/rjags/index.html
- library(runjags) という package もあります → R で JAGS (runjags 編)
- JAGS 雑, library(help = rjags), ベイズ統計 & MCMC も参照

library(rjags) とは
- JAGS (JAGS 雑 も参照) を R から便利に使うための package です
- と言いますか,JAGS を使おうと思ったらこの
library(rjags)経由から使うのがもっとも便利でしょう -
library(rjags)のインストール方法: R を起動して-
update.packages() -
install.packages("rjags")
-
例題で動かしてみる library(rjags)
- 必要なファイル
- 架空データファイル: dummydata.csv
- 列: 細菌密度, log(細菌密度), 食中毒回数, 合計実験回数
- 行: 一被験者 (これは 50 年ぐらい前のアメリカでの人体実験データ)
- BUGS ファイル: infection.bug.txt
- R ファイル: runjags.R
- 架空データファイル: dummydata.csv
架空データをちょっと見る
- 図示するとこんなデータです
- 横軸: log(細菌密度)
- 縦軸: 不本意な割残値 各被験者の食中毒回数 / 合計実験回数
- 不本意さを糊塗するべく
cexで合計実験回数を示している
plot(d$Logdose, d$Positive / d$Total, cex = (d$Total / 6)^2)
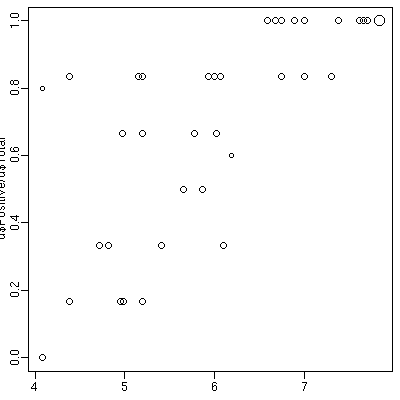
BUGS ファイルの準備
- BUGS 言語でベイズモデルを定義しているファイルを準備する
- WinBUGS とのちがい
- 行末にはセミコロン (;) が必要 (ゐんばぐすではつけてもつけなくてもよい)
- 他は JAGS のマニュアルを参照
- 簡単な例:
infection.bug.txt,random effect 「切片」をもつ混合 logistic 回帰
model
{
Tau.noninformative <- 1.0E-3;
P.gamma <- 1.0E-3;
for (i in 1:N) {
Positive[i] ~ dbin(p[i], Total[i]);
logit(p[i]) <- logit.p[i];
logit.p[i] ~ dnorm(m[i], tau);
m[i] <- beta[1] + beta[2] * Logdose[i];
}
beta[1] ~ dnorm(0.0, Tau.noninformative);
beta[2] ~ dnorm(0.0, Tau.noninformative);
tau ~ dgamma(P.gamma, P.gamma);
}
R のスクリプトを準備する
- R から JAGS をよびだして MCMC 計算をやらせて,その推定結果をうけとる
-
library(rjags)をよみこむ - データとパラメーター 初期値の list を作る
- JAGS に計算を命じる
- 結果をうけとる
-
- 例: 上の
infection.bug.txtを実行する R コード
# データファイルのよみこみ
d <- read.csv("dummydata.csv")
library(rjags) # rjags package のよみこみ
# データ list の準備
list.data <- list(
Positive = d$Positive,
Total = d$Total,
Logdose = d$Logdose,
N = nrow(d)
)
# 初期値 list の準備
inits <- list(
beta = c(0, 0),
tau = 1,
logit.p = rep(0, list.data$N)
)
# R 内でのモデルの定義
m <- jags.model(
file = "infection.bug.txt",
data = list.data,
inits = list(inits, inits, inits),
n.chain = 3
)
# burn-in のためのカラまわし MCMC 計算
update(m, 1000)
# MCMC 計算で事後分布からサンプリング,その結果をうけとる
x <- coda.samples(
m,
c("beta", "tau"),
thin = 100, n.iter = 20000
)
注意
- 実行環境によっては
jags.model()のinits指定がうまくいかない場合もあるようなので,そのような場合はこの行を削除してください (2012-04-02 飯島勇人さんからのご指摘)
R から実行する
-
runjags.Rを R で実行するとこのように表示される
> source("runjags.R")
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 259
Adapting 1000
-------------------------------------------------| 1000
++++++++++++++++++++++++++++++++++++++++++++++++++ 100%
Updating 1000
-------------------------------------------------| 1000
************************************************** 100%
Updating 20000
-------------------------------------------------| 20000
************************************************** 100%
MCMC 計算の結果を調べる
- R の
library(coda)を使う- これは
library(rjags)すると自動的によみこまれる - MCMC 計算の結果処理に便利な
library(coda)については coda 雑 を参照
- これは
- 上の推定計算結果の概要を示してみる
- この架空データを生成するときに使った「真の」パラメーターは下のとおりなので,あまりうまく推定できてないのかもしれない
-
beta[1]= -5.0 -
beta[2]= 1.0 -
tau= 1.0 (事後分布の平均値ではなく中央値と比較せよ)
-
- この架空データを生成するときに使った「真の」パラメーターは下のとおりなので,あまりうまく推定できてないのかもしれない
> summary(x)
Iterations = 2100:22000
Thinning interval = 100
Number of chains = 3
Sample size per chain = 200
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
beta[1] -7.50 1.629 0.0665 0.1085
beta[2] 1.48 0.289 0.0118 0.0197
tau 29.58 245.887 10.0383 12.2574
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
beta[1] -11.065 -8.58 -7.37 -6.31 -4.85
beta[2] 1.008 1.27 1.44 1.66 2.12
tau 0.395 0.81 1.26 2.47 205.84
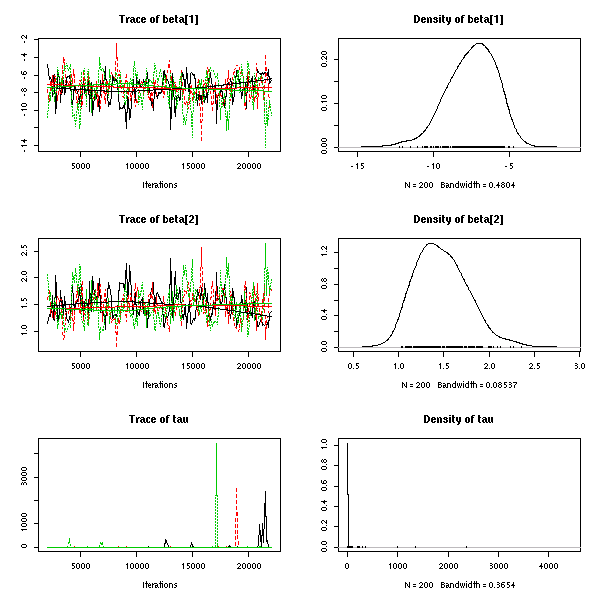
- 図示
> plot(x)
JAGS を直接使う (古いやりかた)
- JAGS を直接つかうには次のファイルが必要である
- cmd ファイル (実行手順指示) : 下記のファイルを指定し,さらに計算ステップ数や出力すべき計算結果を指定するファイル
- bug ファイル (モデルの定義): BUGS 言語で書かれた統計モデルなどの定義
- data.R ファイル: R で書かれた入力データファイル
- init.R ファイル: R で書かれたパラメーター初期値ファイル (必ずしも必要ではない?)
-
jags *.cmd
でcmdファイルを実行する