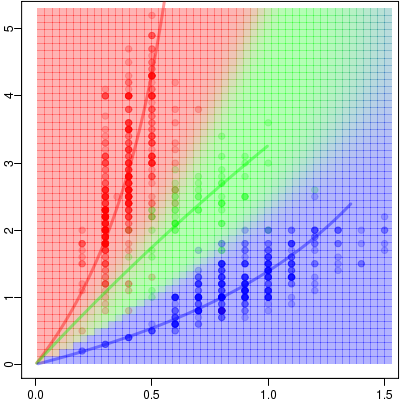
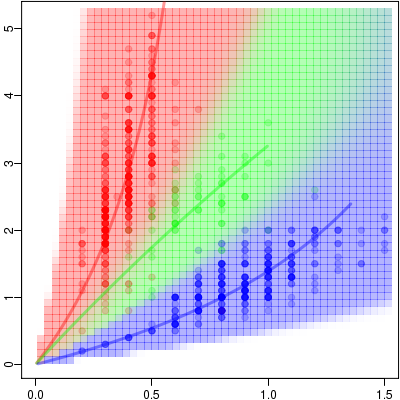
glm()
や
glmmML()
だと「ニセの施肥処理効果」
を発見してしまうけれど,
個体差 + ブロック差の階層ベイズモデルにすると,
「それって単なるブロック差にすぎないんでは」
と指摘する例題を作ってみた.
ようするに,
ブロック差のばらつきが大きいと,
glm()
とかは勝手に「傾向」みたいなものだと錯覚するわけで.
MCMCglmm()
とか私がすきではない
lmer()
とかでも,
個体差 + ブロック差モデルを指定すれば,
ほとんど同じ推定結果を示してくれるわけだが.


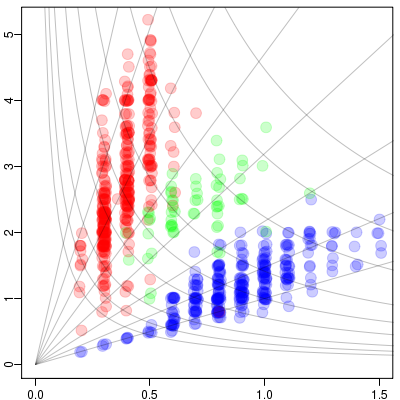
jitter()
とか半透過色指定とかで,
「とびとびの測定値」
の濃度みたいなものがわかる.
そしてこれはタテ・ヨコ比みたいなもので,
葉を分類しましょうという問題なので,
グレイで示してるような座標を考えると妥当なのかも.
原点をとおる直線群は「相似線」といったものであるのにたいして,
双曲線たちは「等面積線」なんだよね.
葉は等形状線にのって成長しているわけではないのだろうから,
そのあたりを考慮する必要あるんだけど.
sqrt(a) 倍・1 / sqrt(a) 倍
すればいいだけ.
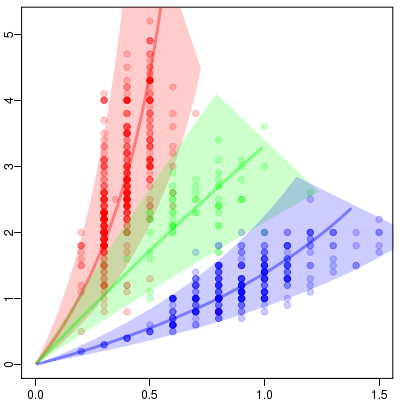
Y[i] ~ dnorm(y[i], Tau.err)
X[i] ~ dnorm(x[i], Tau.err)
y[i] <- unit.length[i] * sqrt(rxy[i])
x[i] <- unit.length[i] / sqrt(rxy[i])
rxy[i] <- exp(log.rxy[i])
log.rxy[i] ~ dnorm(mean.log.rxy[i], tau[Spc[i]])
mean.log.rxy[i] <- (
bs[1, Spc[i]]
+ bs[2, Spc[i]] * (unit.length[i] - Mean.ul)
)
unit.length[i] <- exp(log.unit.length[i])
log.unit.length[i] ~ dnorm(0, Tau.noninformative)
Y[i] ~ dnorm(y[i], Tau.err)
X[i] ~ dnorm(x[i], Tau.err)
y[i] <- unit.length[i] * sqrt(rxy[i])
x[i] <- unit.length[i] / sqrt(rxy[i])
rxy[i] <- exp(log.rxy[i])
log.rxy[i] ~ dnorm(mean.log.rxy[i, spc[i]], tau[spc[i]])
for (s in 1:N.spc) {
mean.log.rxy[i, s] <- (
bs[1, s]
+ bs[2, s] * (unit.length[i] - Mean.ul)
)
}
unit.length[i] <- exp(log.unit.length[i])
log.unit.length[i] ~ dnorm(0, Tau.noninformative)
# spc
spc[i] ~ dcat(q[i,])
Spc[i] ~ dcat(q[i,])
q[i, 1] <- v[i, 1] * w[1] / total.v[i]
q[i, 2] <- v[i, 2] * w[2] / total.v[i]
q[i, 3] <- v[i, 3] / total.v[i]
total.v[i] <- v[i, 1] * w[1] + v[i, 2] * w[2] + v[i, 3]
for (s in 1:N.spc) {
v[i, s] <- exp(
-pow(log.rxy[i] - mean.log.rxy[i, s], 2) * tau[s] * 0.5
) / sigma[s]
}