ぎょーむ日誌 2009-03-(21-31)
2009 年 03 月 21 日 (土)
-
0820 起床.
朝飯.
コーヒー.
洗濯.
怠業.
-
11 時ごろに家をでて,
地下鉄東西線の西 11 丁目駅ちかくの道立近代美術館で
「 セザンヌ主義
父と呼ばれる画家への礼讃
ピカソ・ゴーギャン・マティス・モディリアーニ」
みてきた.
19 世紀
ポスト印象派の画家である
セザンヌ
と,
同時代以降に
彼の方法
をとりいれようとした画家たちの絵を並べた展示.
-
私は
(以下を読めばわかるよーに)
「絵を見る目」みたいなのないし,
美術史にもぜんぜんくわしくないんだけど,
わりとおもしろく見ることできた.
絵についてる解説と実物をながめているうちに,
「あ,この画家たちは人間のアタマの中の
(いわばベイズ統計学的な)
画像処理を検討してるんだ」
といったハナシを思いついてしまったので.
セザンヌたちは賛成しないかもしれないけど.
-
以下,
いつものごとくてきとーなコトを書きますが,
いつものごとくマにうけないように.
まず,
19 世紀以降の画家にとって写真機の技術的発展は
「絵画って何だろな」
と再考させるものだったのではないか,
と.
三次元空間内に配置されたさまざまな光学特性をもつ物体たちに
ある光源からあてた光を反射させて,
どこかの平面上に投影する,
といった変換は写真のほうが精確にみえるからだ.
-
美術史の歴史はよく知らないんだけど,
だったら現物なんかを描くのはヤメて,
宗教画とかにもどります,
とゆーふうにはならなかった.
理由はよくわかんないけど,
ルネッサンス以来の人間中心主義の伝統というか,
画家たちは「人間の認知できる世界」
を描くことに興味あったのかもしれない.
-
さてさて,
写真機と 19 世紀後半に台頭してきた印象派の関係が
いまいちわかんないんだけど,
点描なヒトたちがやってることは絵画の画素 (ピクセル)
化と画素集合に対する
(いわば画像処理ソフトウェアで画素の部分集合の特性値を操作するような)
色変換,
のように見える.
彩色点々の集まりをみた人間は,
アタマの中の画像処理で三次元世界を再構成しうる,
といった絵をみるヒトの
「アタマの中の画像補間機能」
を明示的に援用する方法が欧州近代美術にとりこまれる.
-
で,
写真のようでもなく,
印象派のようでもない方法,
ってのがセザンヌたちの追求した方法ではないでしょーか,
と.
それは平面上に画素化された画像情報が
さらにアタマの中でどう処理されているかを表現したい,
たとえば輪郭抽出とか幾何学的なモデル
(三角形・円筒形など)
あてはめによる構成の把握とか
事前情報にもとづく「二次元→三次元」モデル化とか.
-
妥当な例なのかよくわからんけど
……
点描なヒトたちと比較すると,
肖像画なんかで顔の輪郭線を明示的に示しているように見える.
写真
(これも画素化された二次元上の投影図)
でヒトの顔をみても黒くて太い輪郭線は存在しない.
しかし,
アタマの中では顔のまわりなんかの輪郭線を自動的に抽出・補間してるのではないか
(じつはアタマの中までいかなくても視細胞・視神経系の段階で
エッジ検出を助けるような構造&機能がある……んじゃなかったっけ?).
そういう処理能力があるからこそ,
輪郭線だけで描かれた平板な
(あるいは目なんかを描いていない)
似顔絵とか見ても
「あ,これは誰それの顔だ」
とわかるんでしょーな.
-
同じように,
対象の把握においても幾何学的な遠近法計算
(射影変換つまり座標変換)
は,
アタマの中ではくずされてしまって
「興味がある部分のまわりをまた別の方法で座標変換して拡大」
みたいに処理してるのかも
……
といったあたりを表現したいのが,
セザンヌとかの座標変換してるとしか思えない構図
(人間の顔のパーツの配置とか静物画のモノや台の配置とか)
じゃないのか,
その採用理由の説明のひとつになってないか,
と.
-
このあたりがのちの
キュビズム
と関連してるのかな,
と考えてみたり.
つまりヒトの横顔の片方の目を見てるときも,
われわれは事前情報にもとづいて
「見えてない」もう一方の目がむこう側のこのあたりにある,
とアタマの中の三次元モデル
(三次元なのかな?)
を (いわばベイズ統計モデリング的に) 補間している.
だからこそ,
その横顔が回転してこちらを見たときに
「わっ,このヒトにもやっぱり目がふたつあって,
左右が同じ高さについてたのか」
とかいちいち驚いたりしない.
ピカソとかの横顔なのに二つの目が描かれている絵,
ってのはそういう脳内画像処理をあらわしているのではないのかしらん?
-
その他の仕事はすすまなかった.
うーむ,
一年後ぐらいにこのへんのぎょーむ日誌とか見て
「あらら,盛岡のあとも学会ばてしてたのか」
と思うんだろうな.
今回はそういうへろへろ感はないんですけど.
-
[今日の運動]
-
とはいえ,
うんどう休養日だし
……
天気よかったんで,
札幌市内あちこちかなり歩いたんだけど.
-
[今日の食卓]
- 朝 (0900):
米麦 0.6 合.
キャベツ・ミズナ・ネギ・ハムのサラダ.
- 昼 (1310):
美術館すぐそばのレストランである
プロヴァンサルキムラで美術館展示と連動
セザンヌゆかりの地プロヴァンス地方 19 世紀末レシピを再現する
特別メニュー
を楽しみました.
おいしかった.
- 晩 (2030):
米麦 0.8 合.
ダイコンの味噌汁.
キャベツ・タマネギ・ブナシメジ・豚肉の炒めもの.
2009 年 03 月 22 日 (日)
-
0700 起床.
朝飯.
コーヒー.
洗濯.
怠業.
うー
-
1110 自宅発.
曇.
1130 研究室着.
-
やはり,
どーにもこーにもやるきがないなぁ
……
-
1800 てったい.
買いもの.
1830 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0900):
米麦 0.8 合.
卵焼き.
- 昼 (1230):
研究室お茶部屋.
食パン.
- 晩 (2020):
米麦 0.8 合.
サバの味噌煮.
チンゲンサイ・ジャガイモのスープ.
2009 年 03 月 23 日 (月)
-
0730 起床.
いまいちねむい.
朝飯.
コーヒー.
0840 自宅発.
雪.
さむい.
0855 研究室着.
-
事務室から書類さっさと出してくれ
……
との督促.
しかしぎょーむ日誌によるとすでに 2 週間前に提出ずみ.
で,
先方に調べなおしてもらったら,
やはり提出ずみだった.
ぎょーむ日誌もたまには役にたつ.
-
来週火曜日〆切の「電子情報通信学会誌」の
「講座」の「最近のベイズ理論の進展と応用 (I)」
の久保担当部分「階層ベイズモデルの基礎」
の準備によーやく
とりくんでみる
……
土日はぼーっとしすぎていた.
-
で,
今までみた学会誌投稿規定の中で一番わずらわしい投稿規定を
今さらながらに読んでみる
……
さすがわ,
会員数 4 万名のちょー巨大学会
(蛇足ながら生態学会は 3000 名ぐらい).
いろいろうるさい指示をしてくれる.
何を漢字にして何をひらがなにするか,
とかね.
-
原稿作成技術的な側面でいろいろめんどう
……
とりあえず,
「学会誌」の LaTeX クラスファイルがないんで,
「論文誌」用
のやつでもつかってみるか.
レイアウトが似てるので,
分量みつもりに使えそうだ.
-
といったコマかいごたごたにとりくむ.
-
甲山さんの車の中で半年ほどひそんでいた私の荷物あれこれがでてきた
……
冬用の帽子,手帳,印鑑
……
やっぱりそこにあったのか.
いっぺんお尋ねしてみたのだが.
昨年 10 月
に大雪山北面に登ろうとしたときの荷物.
愛山渓温泉にいろいろ問い合わせたりもしてたんだけど
……
-
さてさて,
電子な通信の学会誌の「講座」記事なのだが
……
2 月の統数研
公開講座
の使いまわしでてきとーにかたづけちまおう,
といった都合のよろしい計画だったんだけど
……
やっぱり文は全部かきなおし,
図も全部つくりなおしが必要,
とゆーかんぢだ.
使いまわせるのは例題だけ.
世の中,
つごーのよろしいハナシってなかなかないもんですね.
-
あまりススまぬまま,
1840 研究室発.
テングザルの松田君がもうすぐ札幌を離れる,
ということで何かごちそうしましょう,
ということでスープカレーになった.
2030 帰宅.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0800):
シリアル.
ヨーグルト.
- 昼 (1200):
研究室.
食パン.
- 晩 (1910):
ピカンティ
の貝カレー.
ここはいつも混んでますな.
2009 年 03 月 24 日 (火)
-
0820 起床.
不調だ.
朝飯.
コーヒー.
空間統計学質問いただいたので,
ちょっとそのあたりを調べてしまった.
-
0945 自宅発.
曇.
今日も寒い.
1000 研究室着.
-
空間統計学
まわりを更新.
-
粕谷さんから連絡いただいたので,
自由集会
ペイジから粕谷さんの
統計学ペイジ
内の投影資料ファイルへのリンクをつける.
線形モデルの交互作用項の解説.
-
昼飯.
お茶部屋の蛍光灯がキレている
……
何やら雑用係に対する圧迫感がわいてきたので,
蛍光灯を取り外して地環研ウラの蛍光灯ごみ捨て場に運び,
事務室会計係で新しいのもらってきた.
-
窓の外は冬のような雪.
-
また別のこんさるメイルかき.
-
そして階層ベイズモデル解説かきが進捗せぬまま撤退.
1910 研究室発.
北海道,
寒気におおわれている.
買いもの.
1930 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
生活周期,
なかなか思うようにコントロールできない
……
-
[今日の食卓]
- 朝 (0900):
米麦 0.6 合.
ピーマン・豚肉の炒めもの.
- 昼 (1320):
研究室お茶部屋.
米麦 0.6 合.
ピーマン・豚肉の炒めもの.
- 晩 (2040):
米麦 0.8 合.
ブロッコリー・ニンジン・タマネギ・シイタケ・干しエビ・鶏肉のスープ.
キャベツ・ネギ・ミズナ・ハムのサラダ.
2009 年 03 月 25 日 (水)
-
0720 起床.
いまいち.
朝飯.
コーヒー.
盛岡からの帰路検討していた,
粕谷さん論文原稿のコメントに関して,
少しアタマが整理されてきたように思えたので,
もうちょっと考えてみる.
0920 自宅発.
晴.
0935 研究室着.
-
午前中はそのコメントメイルかきで終わってしまった.
要点は「確率変数の差 D = X - Y」に関して,
-
D の確率分布 F(D) が「非対称」とは
F(D) の期待値と中央値が一致してないこと
(これはどんな確率分布でもそう言ってよいのでしょう,
たぶん)
-
F(D) が非対称なとき,
F(X) もしくは F(Y) の少なくとも一方は非対称
ということだけです.
以下,
その議論の部分.
(追記:
じつはこの「平均値 != 中央値」の議論は不充分.
3/30のハナシも参照)
さて,本題ですが,D = X - Y と定義される D の確率分布が非対称である状況
を問題にしているわけですが,読者としては「どういう状況で D が左右非対称
になるか」といったことも知りたいのではないかと思います.このあたりの検
討も必要ではないでしょうか.
で,考えてみますと,「非対称」の定義を明確にすべきでしょう.統計学本を
きちんとあたっていないのですが,おそらく非対称の定義は「中央値と平均値
が等しくない」としてよいだろうと思います.
つぎに D の確率分布が非対称になる状況を考えます.ここで D の確率分布(以
下,分布は F(D) のように書きます) の中央値はゼロとおきます (以下の議論
に関しては一般性を失うことなくゼロとおいて良いはずです).このときに,
F(D) が非対称であるためには,F(X) と F(Y) の少なくとも一方が非対称でな
ければならない,といった条件があるのではないでしょうか.
厳密な証明はしていませんが,たぶん以下のように考えればよいように思いま
した.まず F(D) の中央値がゼロであるとき F(X) と F(Y) の中央値は等しい,
といったことが成立しているはずです.
次に F(D) が非対称であることから,F(D) の期待値 (E(D) とします) はゼロ
ではありません.すると E(D) = E(X - Y) = E(X) - E(Y) != 0 から E(X) と
E(Y) の期待値は等しくありません.つまり,F(X) と F(Y) は中央値は同じで
あるにもかかわらず,期待値は等しくないので,F(X) と F(Y) の少なくともど
ちらか一方において,
・中央値と期待値が等しくない
・つまり非対称
ということになります.逆に F(X) と F(Y) の中央値も等しくかつ期待値も等
しければ,E(D) = E(X) - E(Y) = 0 となり,F(D) の中央値・期待値がゼロと
なり F(D) は対称な分布となります.
このことから,「F(D) が非対称となるのはどういう状況か?」と聞かれたとき
に「F(X) もしくは F(Y) のどちらかあるいは両方が非対称なとき (中央値と平
均値が等しくない)」と回答してよいのでしょう.
また F(D) が非対称かどうかを調べるときには F(X) と F(Y) それぞれで中央
値と平均値が等しいかどうかを調べる,といった方法がより有効ではないでしょ
うか (ただし中央値==平均値を調べるのもそれなりにめんどうな気もします).
粕谷さんは F(D) が非対称かどうかを調べたらどうか,と書かれていました.
これはちょっと問題になる場合があるかもしれません.というのも F(X) と
F(Y) が両方とも対称であるにもかかわらず (中央値が等しければ F(D) は対称
となる),中央値が等しくない (帰無仮説が正しくない) 場合には F(D) は非対
称となるからです.
ハナシは少し横にそれますが,上のようなことを書いているうちに,平均値を
使った検定ができないから中央値の検定で代用するといった発想 (が多いんで
しょうかね?) といった考えかた自体が問題になる場合もあるかも,という気
もしてきました.
・中央値が等しいけれど,平均値は等しくない
・平均値が等しいけれど,中央値は等しくない
それぞれ結果に関する生物学的な考察はずいぶんとちがってくる場合もありそ
うですね.
昼飯たべにちょっと帰宅.
午後は 3 時間ほど Pieter Zuidema さん (ユトレヒト大)
あいてに統計モデリングとかの話.
Mark Rees の Integral projection 計算ってそんなにいいもんですかね
(2007-11-13 でも何やら言及してるな).
階層ベイズモデルで対処すべき問題だ.
電子情報通信学会誌の階層ベイズモデル解説かき
にもどろうとしたんだけど,
なかなか
……
そして院生から Zuidema さんを晩飯につれだせ命令が.
皆さんいそがしいので,
一番ヒマそうな私にまわした,
とのことのよーで.
1910 研究室発.
Zuidema さんと JR 札幌駅ビルで晩飯.
2030 帰宅.
[今日の運動]
[今日の食卓]
- 朝 (0830):
米麦 0.6 合.
ブロッコリー・ニンジン・タマネギ・シイタケ・干しエビ・鶏肉のスープ.
- 昼 (1300):
米麦 0.6 合.
ブロッコリー・ニンジン・タマネギ・シイタケ・干しエビ・鶏肉のスープ.
- 晩 (1940):
駅ビルの食堂フロアのひとつ,
ステラプレイス 6F の回転寿司に
(ややウケねらいで)
行こうとしたんだけど,
平日 19 時すぎでも店の外まで「待ち」のヒトたちがびっしり.
皆さん,
ホントに回転寿司すきだよね.
とゆーことで,
スープカレー.
2009 年 03 月 26 日 (木)
-
0740 起床.
ねむい.
ややしんどい.
朝飯.
コーヒー.
0840 自宅発.
曇.
0855 研究室着.
-
Trendy セミナー
の予習.
-
で,0930 よりセミナー.
最初に重定さんで,
拡散係数が場所によって変わる場合
(といっても「一次元のストライプ」的な地形なのだが)
の periodic traveling wave の速度について.
このあたり,
理論的にツメようとすると意外と手間で
(かなり単純化してるのに),
まず空間 vs 局所密度の空間上で envelope なる
front をあらわす曲線を定義し,
さらにある接線の法線 vector をやはり
空間 vs 局所密度空間上に描くとこれはやや単純な
「波形」になるので,
そこから heuristic に定式化した,
と.
で,
近年になってとある応用数学者のヒトが
その heuristic 式が正しいと証明してくれました,
といった次第で.
あと,
拡散係数を正確に推定するためには局所密度の時間変化データが必要,
といったかんぢだ.
-
次は Pieter Zuidemer さんで,
樹木の個体群動態モデル.
「個体差」が重要な個体群動態なんだけど,
階層ベイズモデルを「使わず」になんとかならんか,
といった方向性で.
たとえばサイズ・樹齢を同時に考えたモデルとか.
あるいは Mark Rees (最近は Steve Ellner も参加している)
integral projection matrix (IPA) のハナシとか.
IPA って本質的には階層ベイズモデルだけど,
パラメーター推定のやりかたに問題ありますよ
(多段推定だから),
といったことを指摘せざるをえなかった.
-
電子情報通信学会誌の階層ベイズモデル解説かき,
さすがに時間がなくなってきたのでぢりぢりとススめる.
-
夕方にまた Pieter Zuidemer さんとベイズモデリング相談.
-
1950 研究室発.
買いもの.
2020 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0800):
米麦 0.8 合.
キャベツ・ネギ・ミズナ・ハムのサラダ.
- 昼 (1250):
研究室.
食パン.
- 晩 (2130):
米麦 0.8 合.
チンゲンサイ・ショウガ・ニンジン・ホタテのスープ.
ダイコン・鶏肉の煮もの.
2009 年 03 月 27 日 (金)
-
0800 起床.
朝飯.
コーヒー.
0900 自宅発.
曇.
0915 研究室着.
-
朝から晩まで
電子情報通信学会誌の階層ベイズモデル解説かき,
-
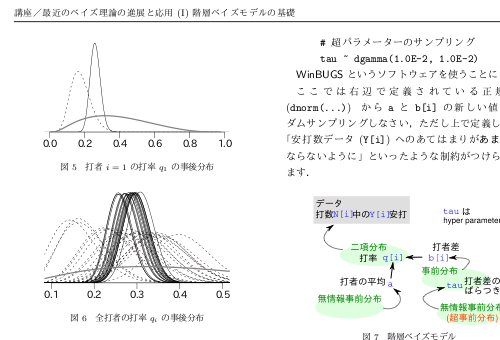
こんなかんぢで進行中.
蛇足ながら,
下の図はまちがい,
と気づいたのであとで修正した.
-
昼飯.
-
4/2 (木) の会議の通知がきたので,
そっこーで「欠席します」と連絡.
-
R の
median() はどうやって
中央値を計算してるんだろう,
というのを調べる必要があって
……
中間さんサイトで
検索
して読解してみたところ,
たとえば
c(-1.5, -1.5, 1, 2)
といったデータの場合,
真中のふたつ -1.5 と 1 の平均値である-0.25
を median としている,とわかった.
-
ベイズ解説かき,
主観的には 7-8 割おわったかな,
とゆー状況で撤退.
2115 研究室発.
2130 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
来月・来年度からはけんこうな日々になるのだろうか
……
-
[今日の食卓]
- 朝 (0830):
米麦 0.6 合.
チンゲンサイ・ショウガ・ニンジン・ホタテのスープ.
- 昼 (1310):
研究室お茶部屋.
米麦 0.6 合.
ダイコン・鶏肉の煮もの.
- 晩 (2210):
米麦 0.6 合.
チンゲンサイ・ショウガ・ニンジン・ホタテのスープ.
ヨーグルト.
リンゴ.
2009 年 03 月 28 日 (土)
-
0750 起床.
うー.
朝飯.
コーヒー.
洗濯.
怠業.
-
さっさと原稿かきのつづきを
……
しかしなんとも書く気が
……
けっきょく昼飯くって
1315 自宅発.
曇.
1400 研究室着.
-
電子情報通信学会誌の階層ベイズモデル解説かき
……
-
1745 文章の部分はひととーりかけた,
よーに思える.
-
図とかの細かい修正.
-
まー,
今回は合計 5 ペイジなんで,
「何を削るか」
が重要なんだよね.
けっきょく MCMC についてはほとんど説明できなかった.
ゐんばぐすについても.
そこでこの解説記事のサポートペイジなんかを作ってみた.
-
作文の推敲はまだまだ必要,
という気がするけど
……
〆切である次の火曜日まで少し放置して,
この作文との距離をおいたほうが良さそうだ.
撤退.
2000 研究室発.
買いもの.
2030 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
げんこーもひとまずオワったことだし,
明日こそはうんどうを
……
!
-
[今日の食卓]
- 朝 (0900):
米麦 0.8 合.
ニラ・卵の炒めもの.
- 昼 (1300):
米麦 0.8 合.
ニラ・卵の炒めもの.
- 晩 (2130):
米麦 0.6 合.
ニラ・キャベツ・タマネギ・シイタケ・ブナシメジ・鶏肉の
キムチスープ.
2009 年 03 月 29 日 (日)
-
0830 起床.
今朝もねむいです.
朝飯.
コーヒー.
怠業.
-
電子情報通信学会誌の階層ベイズモデル解説かき
は昨日,
ひととーり何とかオワったわけだし
(まだ推敲が必要だけど),
今日はなんとしてもうんどうしなくては
……
-
しかしあまりにも長きうんどう不足な日々で,
うんどうにふみきる心理的障壁はあまりにも高く
……
-
ちょっとうんどうしてから,
ひさびさの北大構内走にでてみる.
時刻は 1155.
天気はよい.

[北大構内メインストリート]
は雪がほとんど残っていないわけだが.
ところで,
やはりひさしぶりに走るのは危ない.
自宅をでてちょっと走って信号まちのために
立ち止まったら 1-2 秒ほど立ちくらみ状態になってしまった.
ゆっくり走る.

[低温研-獣医学部前]
このエルムトンネル上の
軟舗装歩道はまだ雪におおわれてますな.
この近くの建物で応動昆の大会が開催されてるので,
昆虫生態学者に見つからぬように注意しなくては
……
いやいや,
ヒトを見たらこんさるくらいあんとと思え,
といった被害妄想にとりつかれてるな.

[さらにその先]
つまりトンネル上部の西側はこんなかんぢで.
数日前にも雪ふったもんなぁ.

[北大の陸上競技場]
そこで,
歩道からちょっとそれて北大の
400 m トラック (アメフト競技場でもあるのだが)
を三周ばかりてけてけ走ることに.
ここの土の上を走るのはいいかんぢ.
-
1235 帰宅.
40 分間ほど走った.
けっこうばてばて.
まあ,
ゆっくり「りはびり」していくほかあるまい.
シャワー & 昼飯.
1350 自宅発.
晴.
1405 研究室着.
-
研究室にきてはみたものの,
何だかぽーっとしてしまって,
何ごとも進捗せづ.
-
とりあえず現状をまとめてみよう.
まずは論文まわり系:
-
宮田さん論文:
これが最優先.
放置しとくと危険,
とゆー気がする.
-
アリけんか論文の再投稿:
いらん discussion を削って
全体を短くし,
石狩浜問題 (がそんなに重要かどうかはともかく)
に専念.
行動連鎖らしきものはあえて軽くあつかう.
こないだ大統領に廊下でばったりあったら
「Animal Behavior にでもだせば」
といったご意見のよーで.
-
ウミガメ論文:
現時点ではまだカゲもかたちもない.
生態学会盛岡大会でポスター発表したときの感触から,
これはやはり統計モデリング手法の論文
(ウミガメは単なる材料のひとつ)
という方向でまとめたほうがよさそう.
ちかごろ階層ベイズモデル特集をやった
Ecological Applications とか,
手法の論文がとおりやすい Ecology Letters
あたり,
やや高めに目標を設定するつもり.
-
お花見おサル論文:
まあ,
これは霊長研にうつった松田君におまかせ.
-
屋久島葉寿命論文:
これの再解析はちょー難問,
の可能性あり.
かなりしんどそう.
難しいのはかまわないんだけど,
問題は「時間かかりそう」な
(& 督促者がキビしくない)
仕事がついついあとまわしになりがちで,
いつまでたっても着手されない現状だ.
-
次にもの書き・計算したうけ系:
-
R 作図わざ本: 編集者コメントを反映させる作業をいっきに
やってしまいたいところだが
……
これは「毎日ぽちぽち作業」でどうにかならないだろうか,
という私にとっては実験的な方法で処理してみる予定.
うまくいくのだろうか?
-
岩波統計学本: R 作図わざ本のつぎに着手.
-
上の二件が片づくまでは日本語作文ぎょーむは
もうやりたくありません状態.
-
あ,しかし例の電子情報通信学会誌のベイズ解説の
原稿は推敲して,
ごちゃごちゃ
うっとうしい書類その他もつけて,
次の火曜日〆切に提出しなくては.
これまた,
いろいろ修正しろと言われるんだろうな
……
-
帯広樹木開花の時系列解析: これはいったん着手すると,
終了するまでにいったい何日かかるのか不明なので,
こわくて着手できないといった状況.
-
Cao さんデータ解析: この国際救助隊活動も
「どんだけ時間かかるの?」
不安は上と同様なのだが,
いちおう 4 月には着手すると言ってしまったので,
着手せざるをえない.
帯広したうけとは異なり,
さいわいにもデータ構造は簡単そう.
結果はどうなるのかわからんけど.
-
ともかく 2009 年度は計算したうけを増やすと危ない,
自滅的,
と考えるべきだろう.
-
最後に雑用系:
-
査読ぎょーむ.
4/6 (月) しめきり.
-
生態学会さーばー移行作業.
これは私が主導的にやらねばならないネット雑用.
かなり気をつけて慎重にやる必要あり.
しかもさっさと終了させねばならない.
気がおもい.
-
ネット雑用といえば,
ここ A 棟耐震工事期間のさーばー退避問題があった.
5 月ぐらいに着手,
でまにあうかな?
-
耐震工事疎開生活の準備といえば,
ゴミすて作業がまだある.
まあ,
これはぽちぽちと
……
-
これだけ?
まあ,
新年度になったら研究室まわりの細かいネット雑用はあるだろうけど
……
書き出してみると雑用系が意外と少なく,
少しだけ気がラクになった.
-
しかし生態学会さーばー移転雑用はしんどい.
-
ほかにも
「やらなくてもダメになるわけではないんだけど,
やったほうが良い」
ネットまわりの用件いろいろあるのだが
……
まあ,
当面はムリそう.
-
で,
さっさと何かにとりかかればよいのに,
(やはり原稿提出〆切日がちかい)
斎藤君とお茶部屋でとりとめもない外来種雑談,
けっこう長時間.
-
ということで,
本日は何も進捗しなかった.
1820 研究室発.
1850 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
腹筋運動 30 ×
3 回.
背筋運動 30 ×
3 回.
腕立ふせ 10 ×
3 回.
北大構内走 40 分間.
ストレッチ.
-
[今日の食卓]
- 朝 (0900):
シリアル.
ヨーグルト.
- 昼 (1320):
研究室お茶部屋.
米麦 0.8 合.
- 晩 (2020):
米麦 0.8 合.
タマネギ・ジャガイモ・油揚の味噌汁.
ホッケのショウガ味噌煮.
2009 年 03 月 30 日 (月)
-
0800 起床.
朝飯.
コーヒー.
0910 自宅発.
曇.
0925 研究室着.
-
いろいろ雑用めいる書き.
昨日の日曜日のうちにやっておけばよかった.
-
たとえば,
電子情報通信学会誌から
「写真貼れ」書類を郵送しろと命令されてるんだけど,
これってどうにかなりませんかね
……
とお尋ねしてみたところ,
画像ファイルでもヨシとの連絡いただいた.
やれやれ.
だったら最初からそう連絡してくださいよ.

[「写真貼れ」書類]
「著者自己紹介」とやらで,
おそらく手書きで原稿用紙ふうマス目に自己紹介をうめ,
写真をとって現像して適切な大きさに裁断して,
書類左下にぴったり貼りつけなさい,
といった趣旨の書類.
電子情報通信
学会がコレではいかんのではないでしょうか
……
あるいは「電子情報通信学」
の限界に絶望しているから,
紙にこだわっているのかなぁ
……
-
さっさといろいろなぎょーむ
3/25
のギロンのつづきの検討に時間を使ってしまった.
-
かなり時間かかったけど,
なかなか (ふつーの統計学の教科書にはいちいち記載してない)
ちょっと面白いことがわかった.
確率変数 X, Y の差の D (= X - Y) の確率分布が「対称」
になるかどーか,
といったハナシ.
3/25
のときには「非対称なら中央値 != 平均値」でしょ」
と決めつけてハナシをしてたんだけど,
これではダメとわかったので
(中央値 == 平均値であっても非対称な場合がある),
もう少し別の方向から考えてみた.
-
結論としては,
-
X, Y の確率分布が同じ (もしくは「同じ分布がヨコにずれた」関係)
であるときには,
D はつねに対称な確率分布となる
-
上の条件を満たさないときには,
X と Y の確率分布がどちらも対称であるときにしか,
D は対称な分布にならない
これだけのことを述べるのに,
下のごときぐだぐだとした検討が必要とされる.
といっても,
「D の分布ってたたみこみ (convolution)
で書いてみて,ひねくったらどうなんでしょ」
といった高校数学 + αなハナシだけなんだが.
えーい,
しかしながら,
正確な数学的証明としてはまだまだ不充分なんだろうな
……
(後記:
やはり下はまちがっていて,
そもそも「h(D) の中央値がゼロなら,f(X) と g(Y) の中央値が等しい」
といったハナシも正しくない
……
4/3)
ともあれ,「平均値 != 中央値」の方向から D = X - Y の分布の非対称性に
ついて議論するのはまずい方策らしい,とわかってきました.
そこでちょっと別の方法を考えてみました.
まず,議論のそもそもの出発点として D の非対称性を事前に調べて,というの
はまずいだろう,という考えがありました.これは標本 X と標本 Y の母集団
がどちらも対称な分布であったとしても,母集団の中央値が異なっていれば,
D は非対称になるからです.いま調べたいのは D の中央値がゼロである場合
です.
D の確率分布の中央値がゼロであるためには X, Y それぞれの確率分布の中央
値が等しくなければなりません.そこでいま,これらが共通の中央値 c をもつ
とします.
「対称な確率分布」は次のように定義します.D, X, Y それぞれの確率密度関
数を h(D), f(X), g(Y) とします.それぞれの中央値は 0, c, c なので,こ
れらが対称であるときにだけ,
h(Δ) = h(-Δ)
f(c + Δ) = f(c - Δ)
g(c + Δ) = g(c - Δ)
が成立している,と定義します.
さて h(Δ) と f(X), g(Y) の関係を考えてみると,X = Δ + Y であることから,
h(Δ) = ∫f(Δ + y) g(y) dy
h(-Δ) = ∫f(-Δ + y) g(y) dy
と畳みこみのかたちで定義されます.
まずは f(X) と g(Y) が同じ確率分布であるとき (g(Y) = f(Y)) について考え
ます.h(-Δ) の式において y = z + Δ とおくと,
h(-Δ) = ∫f(z) f(z + Δ) dz
となり
h(Δ) = ∫f(Δ + y) f(y) dy
と同じなので,h(Δ) = h(-Δ) となります.つまり f(X) と g(Y) が同じ確率
分布であるときには h(D) は常に対称である,ということがわかります.
また g(Y) は f(X) を「ずらした」確率分布であるとき,つまり
g(Y) = f(Y + 定数)
であるときにも上と同じ論法で h(D) は対称な確率分布となります.この場合
は当然ながら f(X) と g(Y) の中央値は等しくありませんし,h(D) の中央値は
ゼロではありません.
つまり一般には,f(X) と g(Y) が「同じ確率分布をずらした (あるいはずら
さない) 関係」にあるときには,つねに h(D) は対称となります.
次に f(X) と g(Y) が「同じ確率分布をずらした関係」ではない場合について
考えます.
h(Δ) = ∫f(Δ + y) g(y) dy
において,y を「ずらして」 y = c + z とおくと,
h(Δ) = ∫f(c + (z + Δ)) g(c + z) dz
となります.また -Δ = X - Y のときには
h(-Δ) = ∫f(-Δ + y) g(y) dy
となり,今度は y = c - z とおいて書き変えると
h(-Δ) = ∫f(c - (z + Δ)) g(c - z) dz
となります.
f(X) と g(Y) が同じ確率分布ではないときに,h(Δ) = h(-Δ) であるために
は,
f(c + (z + Δ)) = f(c - (z + Δ))
かつ
g(c + z) = g(c - z)
が必要とされ,これが成立するのは f(X) と g(Y) がどちらも対称である場合
なので,
h(D) が対称 ⇔ f(X) と g(Y) のどちらも対称
と言えるのではないかと思います (必要十分性の確認がいいかげんですが).
まとめますと,f(X) と g(Y) の中央値が等しい (どちらも c) ときに,
中央値ゼロの確率分布 h(D) が対称であるためには,f(X) と g(Y) が対称であ
るかどうかを確認すればよい,そして f(X) と f(Y) の対称性はそれぞれの中
央値とは関係なくチェックできます.
ただし f(X) と g(Y) が同じ確率分布である (中央値が等しい),もしくは
g(Y) = f(Y + 定数) といった関係にある (中央値が等しくない) ときには,
f(X) と g(Y) が非対称であっても h(D) は対称となります.
ということで,h(D) がどういうときに対称になるのか,をひととおり整理で
きているのではないかと思います.
昼飯.
時刻はすでに 14 時すぎ.
窓の外は雪.
電子情報通信学会誌の階層ベイズモデル解説,
みなおし.
甲山さんまわりのメイルアカウントうんぬん問題あれこれ
に一時間ばかりふりまわされる.

[3 月末の降雪]
窓の外の雪,
いつのまにかどんどん大雪に.
-
解説みなおし終了.
なんだかばかばかしい書類一式をととのえて,
原稿できました連絡.
あとはダウンロードしてください,
ってことで.
-
1820 研究室発.
雪.
買いもの.
1850 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0830):
米麦 0.6 合.
キャベツ・鶏肉の炒めもの.
- 昼 (1410):
研究室お茶部屋.
米麦 0.8 合.
キャベツ・鶏肉の炒めもの.
- 晩 (2100):
米麦 0.6 合.
ダイコン・ナメコの味噌汁.
キャベツ・ネギ・ハムのサラダ.
2009 年 03 月 31 日 (火)
-
0750 起床.
朝飯.
コーヒー.
0850 自宅発.
ちょっと雪.
0905 研究室着.
-
メイルかきに時間とられた.
また電子情報通信学会誌方面から
ヘンなわーど書類だせとか言ってくるし
……
-
で,
今日は夜まで生態学会さーばー移行問題にとりくんでいた.
しかも本日は「新さーばーで遊んだ」
「さーばー屋さんにいろいろおしえてもらった」
「せいたい学会事務局と竹中さんにたくさんメイルをかいた」
でオワった
……
-
新さーばーの管理ゆーざーインターフェイスは
Plesk,
まあ以前の
TLAS
よりはかっちょいいし,
高機能だし (必要な機能かどうかはともかく)
……
しかし,
あいかわらずシバりが多いね.
-
ユーザー (Plesk ではなぜかクライアントと呼称)
とかメイリングリストとか作ったりぶっ壊したりして遊んでるうちに,
だいたいのしくみがわかってきた
……
-
さーばー移行の手順,
現時点の腹案.
-
www.esj.ne.jp
こんてんつの移行.
Plesk は使わないで adduser
とかでドロくさくやったほうがよいかも.
Plesk 使わない利点は自由自在にできる,
というあたり.
欠点は他人に引きつぐのがめんどうになる,
というあたり.
さーて,
どうしたもんだか.
-
なんだか趣旨不明な
www.e-eafes.org
の移行.
まあ,
これは単純作業になるはず.
-
mail.esj.ne.jp
の移行.
これはかなり苦闘するかも.
-
ぢつはどの作業においても DNS server の設定が重要になる.
過去の苦闘
記録
にあるように,
これって旧さーばー上の DNS server にあれこれ設定されてしまってるんだよね.
これをさーばー屋さんの DNS server に移行しなければならない,
と.
-
えーと,
旧さーばーの DNS 設定おき場は
/var/lib/named/etc/named/
以下,
か.
-
さーばー雑用ばっかりやってると,
なんともすさむので,
ときどきお茶部屋に逃げる.
ブナ林データ解析雑談,
とか.
-
2020 研究室発.
2035 帰宅.
晩飯.
ぐったり.
-
[今日の運動]
-
うーむ,
いともたやすく
うんどう不足状態におちいるな
……
-
[今日の食卓]
- 朝 (0830):
米麦 0.8 合.
ダイコン・ナメコの味噌汁.
キャベツ・ネギ・ハムのサラダ.
- 昼 (1330):
研究室お茶部屋.
食パン.
キャベツ・ネギ・ハムのサラダ.
- 晩 (2130):
米麦 0.8 合.
ダイコン・ナメコの味噌汁.
キャベツ・ネギ・ハムのサラダ.