-
0820 起床.
ちょっと寒くて
寒くて 0600 ごろいったん目ざめてしまった.
朝飯.
コーヒー.
洗濯.
うんどう.
-
青木さんの
統計学関連なんでもあり
掲示板で「0項の切れた分布」のパラメーター推定に関する質問があって,
どうなることやらと見てたんだが
……
library(VGAM)
使えばいいんでは,
という提案があった.
この策にはまったく気づかなかったので
(私は
optim() で最尤推定すればいいぢゃん,
などと考えてた),
さっそく自分の手もとで試してみた.
-
そもそも「0 項の切れた (ポアソン) 分布」
とはこういうデータのことである.
> v.sample <- rpois(1000, exp(-1))
> y <- v.sample[v.sample > 0]
> cat("# length(y) =", length(y), ", mean(y) = ", mean(y), "\n")
# length(y) = 303 , mean(y) = 1.1650
ポアソン乱数なんだけど,
ゼロを含んでいない.
もともとの (ゼロをふくむ) ポアソン分布の平均値は
exp(-1) ∼ 0.368
なんだけど,
ポアソン分布のゼロぬき条件つき期待値は
exp(-1) / (1 - exp(-exp(-1))) ∼ 1.20
となる
(上で示しているように標本平均は 1.17
……
VGAM の Pospois
記述も参照).
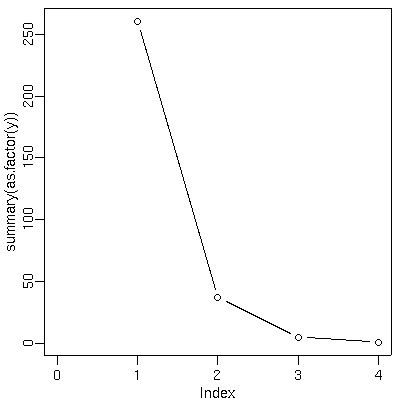
# 正確には xy <- as.factor(y); plot(as.numeric(names(xy), xy, ...)
# とすべきなんだろうけど……
> plot(summary(as.factor(y)), type = "b", xlim = range(0, y))
ここから GLM
的な推定をやって (log link 関数内の)
intercept = -1 を推定できるかどうか,
という問題.
-
言うまでもなく,
この平均値が大きいポアソン分布では「データがゼロを含まない」
という条件はあまり重要ではない.
そもそもゼロという値が出現する確率は小さいのだから.
「0 がない」という条件つきポアソン分布を考慮しなければならないのは,
分布の平均が (この例題のように) 小さい場合である.
-
推定じたいは簡単で,
ふつーの
glm()
的にやればよい.
> library(VGAM)
> fit1 <- vglm(y ~ 1, family = pospoisson())
family = pospoisson()
で「つねに正値をとるポアソン分布」をばらつきの分布関数にしている.
-
推定結果を
summary(fit1)
するとこうなってた.
Call:
vglm(formula = y ~ 1, family = pospoisson())
Pearson Residuals:
Min 1Q Median 3Q Max
log(lambda) -0.396 -0.396 -0.396 -0.396 6.81
Coefficients:
Value Std. Error t value
(Intercept) -1.16 0.138 -8.4
Number of linear predictors: 1
Name of linear predictor: log(lambda)
Dispersion Parameter for pospoisson family: 1
Log-likelihood: -106.73 on 302 degrees of freedom
Number of Iterations: 5
推定値は -1.16
でまあまあ正確には推定できてる.
AIC は自動的に算出できないので,
こいうふうに計算するしかなさそう.
> -2 * logLik(fit1) + 2 * fit1@rank
[1] 215.47
vglm()
の出力は S4 class なので @
を使って slot の値を取りだす必要がある.
slotNames(fit1)
参照.
-
ついでにふつーの 0 も含むポアソン分布による推定と比較してみよう.
fit2 <- vglm(y ~ 1, family = poissonff())
fit3 <- glm(y ~ 1, family = poisson())
えーと,
上の fit2 が vglm() によるもので
Call:
vglm(formula = y ~ 1, family = poissonff())
Pearson Residuals:
Min 1Q Median 3Q Max
log(mu) -0.153 -0.153 -0.153 -0.153 2.63
Coefficients:
Value Std. Error t value
(Intercept) 0.153 0.0532 2.87
Number of linear predictors: 1
Name of linear predictor: log(mu)
(Default) Dispersion Parameter for poissonff family: 1
Residual Deviance: 38.803 on 302 degrees of freedom
Log-likelihood: -336.87 on 302 degrees of freedom
Number of Iterations: 4
fit3 はふつーの glm()
によるもの.
Call:
glm(formula = y ~ 1, family = poisson())
Deviance Residuals:
Min 1Q Median 3Q Max
-0.157 -0.157 -0.157 -0.157 2.049
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.1527 0.0532 2.87 0.0041
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 38.803 on 302 degrees of freedom
Residual deviance: 38.803 on 302 degrees of freedom
AIC: 675.7
Number of Fisher Scoring iterations: 4
fit2
と
fit3
の推定結果は一致している
(推定値だけでなく,
調べてみるとわかるんだけど最大化対数尤度も).
やはり「0 が見えないカウントデータ」
でふつーのポアソン分布を使った推定はまずくて
(特に平均値が小さいとき),
vglm(..., family = pospoisson())
する必要がある,
ということだ.
-
昼飯.
1340 自宅発.
晴.
寒い.
1400 研究室着.
-
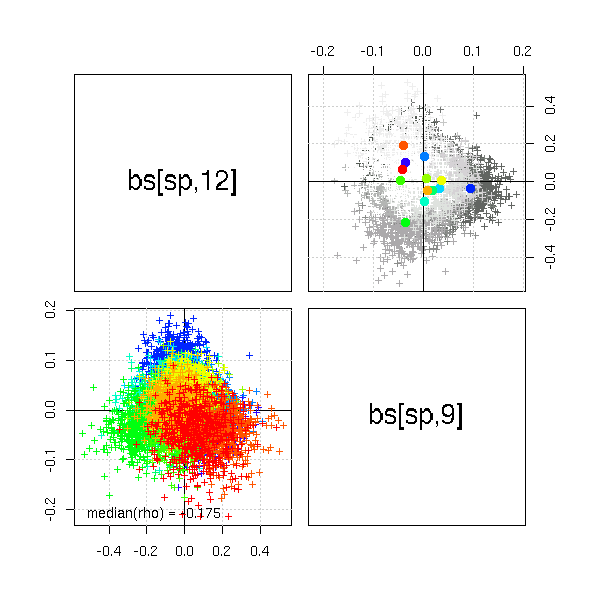
5.6 時間ついやして 12000 MCMC step の熱帯林再計算が終了してた.
-
ウミガメモデルの説明を
……
書こうとする努力.
-
12000 MCMC step の熱帯林再計算のまた再計算.
-
とりあえず,
ウミガメモデルの図.