群集生態学 (community ecology) の多変量解析本．
入手方法は
online
がもっとも無難でしょう．
最悪の多変量解析というべき DCA (を濫用してるのはもはや日本人だけか?)
の難点を示し，
NMDS をススめるもの．
これに近い和書としては，
生物群集の多変量解析
(小林四郎 1995)
だろーけど (NMDS は登場しない)，
出版社である蒼樹書房ごと消えてしまった．
群集生態学 (community ecology) の多変量解析本．
入手方法は
online
がもっとも無難でしょう．
最悪の多変量解析というべき DCA (を濫用してるのはもはや日本人だけか?)
の難点を示し，
NMDS をススめるもの．
これに近い和書としては，
生物群集の多変量解析
(小林四郎 1995)
だろーけど (NMDS は登場しない)，
出版社である蒼樹書房ごと消えてしまった．
library(MCMCglmm)
を使った GLMM のパラメーターの MCMC サンプリングを複数回
(3 回とか)
を独立にやる
library(R2WinBUGS)
が定義する bugs
オブジェクトに変換する
bugs オブジェクトに変換すれば，
Gelman-Rubin の R-hat の計算とか，
あるいはいろいろな図示がラクになる
……
といったもくろみ．
lmer() なんかは使うのヤメて，
MCMCglmm() を!」
とススめているんだけど
(皆さん WinBUGS とか JAGS なんかを使用すると，
なぜかしら健康をいささか損なうおそれがある
……
といった迷信にとりつかれているようなので)
……
いつものごとく「あーいえば，こーいう」といいますか，
「これってどうやってサンプリング数とか決めたらいいんですか?!」
といかにも院生じみた質問・詰問ばかりが返ってくる日々に，
はなはだしく疲労困憊してしまったため．
library(MCMCglmm)
burnin <- 1000
thin <- 50
nitt <- 1000 * thin + burnin
n.chain <- 3
list.MCMCglmm <- lapply( # ここは並列化したほうが良い
1:n.chain,
function(chain) MCMCglmm(
cbind(peak_no, flower_no - peak_no) ~ log(stem_Do) * sex,
random =~ stem_id + ind_id,
data = d, family = "multinomial2",
pr = TRUE, # !!! これはめんどうのもと (後述) !!!
nitt = nitt, thin = thin, burnin = burnin
)
)
source("merge.MCMCglmm.R") # 関数定義ファイルのよみこみ
post.bugs <- merge.MCMCglmm( # 変換
list.MCMCglmm,
n.iter = nitt, n.burnin = burnin, n.thin = thin
)
以上のように R 内で実行して，
いつものごとく plot(post.bugs)
などとやると，
以下のように図示されたりする．
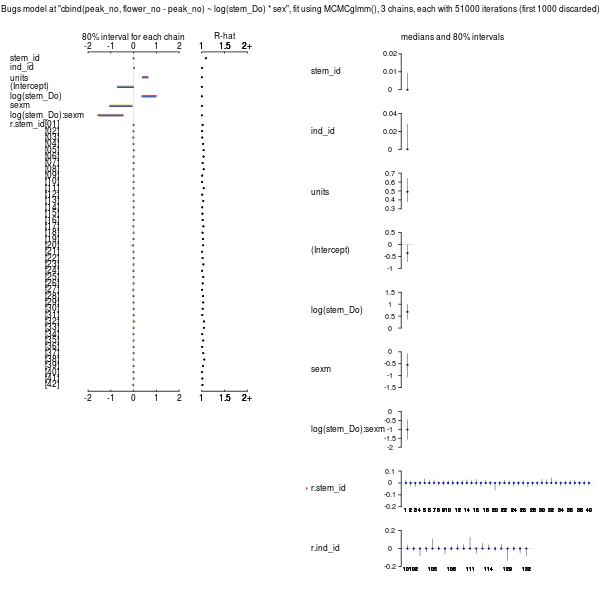
print(post.bugs, digits.summary = 3)
すると以下のように出力される．
Inference for Bugs model at "cbind(peak_no, flower_no - peak_no) ~ log(stem_Do) * sex", fit using MCMCglmm(),
3 chains, each with 51000 iterations (first 1000 discarded), n.thin = 50
n.sims = 3000 iterations saved
mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff
stem_id 0.005 0.019 0.000 0.000 0.000 0.000 0.063 1.089 28
ind_id 0.012 0.042 0.000 0.000 0.000 0.000 0.139 1.008 280
units 0.502 0.102 0.332 0.429 0.491 0.565 0.727 1.001 3000
(Intercept) -0.357 0.288 -0.930 -0.549 -0.350 -0.164 0.203 1.001 3000
log(stem_Do) 0.680 0.257 0.161 0.508 0.678 0.853 1.188 1.001 2600
sexm -0.551 0.386 -1.310 -0.810 -0.549 -0.300 0.201 1.001 3000
log(stem_Do):sexm -1.012 0.438 -1.862 -1.303 -1.008 -0.710 -0.167 1.001 3000
r.stem_id[01] 0.007 0.077 -0.105 0.000 0.000 0.001 0.193 1.018 3000
r.stem_id[02] -0.003 0.070 -0.149 -0.001 0.000 0.000 0.118 1.006 3000
r.stem_id[03] -0.010 0.079 -0.217 -0.001 0.000 0.000 0.086 1.010 2800
r.stem_id[04] -0.004 0.064 -0.143 -0.001 0.000 0.000 0.106 1.029 1500
r.stem_id[05] 0.010 0.074 -0.091 0.000 0.000 0.001 0.213 1.041 470
r.stem_id[06] 0.003 0.067 -0.122 0.000 0.000 0.001 0.174 1.038 1200
r.stem_id[07] 0.009 0.074 -0.079 0.000 0.000 0.001 0.172 1.018 3000
r.stem_id[08] -0.004 0.066 -0.168 -0.001 0.000 0.000 0.114 1.042 1400
r.stem_id[09] 0.000 0.067 -0.124 0.000 0.000 0.000 0.128 1.010 2600
r.stem_id[10] 0.003 0.070 -0.109 0.000 0.000 0.000 0.145 1.007 3000
r.stem_id[11] 0.004 0.079 -0.118 0.000 0.000 0.001 0.154 1.041 670
r.stem_id[12] -0.004 0.071 -0.162 -0.001 0.000 0.000 0.114 1.011 3000
r.stem_id[13] 0.002 0.069 -0.126 0.000 0.000 0.001 0.142 1.033 1700
(略)
MCMCglmm → bugs
オブジェクト変換で面倒なのは，
pr = TRUE と指定したときに MCMC サンプリングされる，
いわゆる random effects なパラメーターの名前を書き換えねばならぬところ．
MCMCglmm オブジェクト
(注: pr = TRUE と指定して生成したもの)
が x であるとすると，
x$Sol という行列には
"stem_id.i01",
"stem_id.i02",
"stem_id.i03", ...
といった列名 (colnames)
で MCMC サンプルが格納されているので，
これを
sub("(.+_id)(\\.)([A-Za-z_]*)([0-9]+)", "r.\\1[\\4]", ...)
といったかんじの
呪術的
というしかない R 正規表現で置換した．
r. という文字列をつけたのは，
これをやっとかなないと plot(post.bugs)
がエラーになるため
……
さらに，
これらの添字が 1 から始まる通し番号でないときには，
plot(post.bugs) の左パネルには正しく図示されないみたいだ．
上の図でも ind_id は示されていない
(右パネル一番下には図示されているが)．
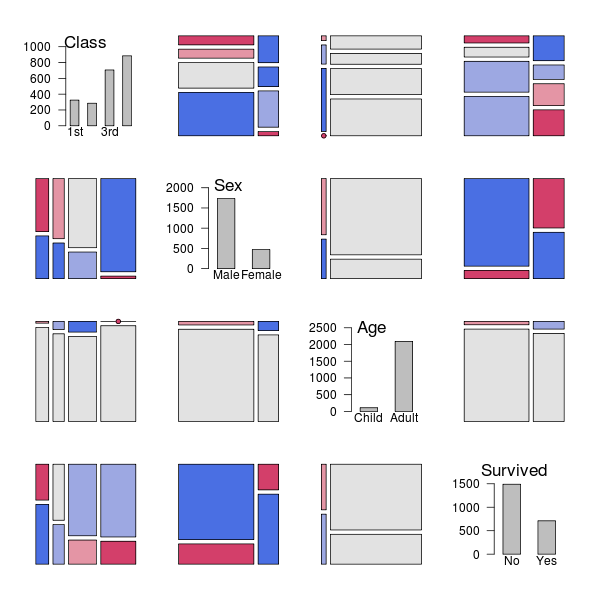
mosaicplot()
とか
plot.table(),
spineplot() とかかな．
library(lattice)
で 検索
すると barchart.table()
(総称関数 barchart)
……
まだインストールしてないけど，
library(vcd)
にはいろいろな関数が用意されてるみたいだ．
vcd とは visualizing categorical data とのこと．
demo(package = "vcd")
もいろいろ準備されてるな．
これはタイタニック号遭難事件時の，
客室等級・男女別・年齢ごとの生死．
library(bipartite)
の plotweb()
とか．
これはすごい．
以前，
苫小牧にいた平尾君も同様の関数を作ってはいたのだが
(ぎょーむ日誌 2005-03-17)．
統計モデルの利用に関してはこれまでは推定ばかりが重視 される傾向にありました．その根底にあるのは，なんでもい いから，とにかく手元のデータにあてはまりが良いモデルを 探し出せばそれでよい，という発想です．統計ユーザーのほ とんどはこう考えているのではないでしょうか． これに対して，モデル選択は予測を重視する発想にもとづい ています．予測とは， 同じサンプリングをやったときに，つぎに出現するデータ へのあてはまりが良いデータを作る ということです．このときの制約条件としては，「たまたま 手元にある」観測データにもとづいて，予測のためにモデル を作りなさい……というややしんどいものです． したがって，モデル選択の目的は真のモデルを構築すること ではありません．真のモデルと同等のモデルを作るためには 無限のデータが必要になります．手元にある限定的な情報だ けをくみあわせて，予測のための統計モデルを作るので，こ れは真のモデルより簡単なものになります． この難しいモデル選択を簡便にすませてしまおうというのが AIC や DIC といったモデル選択規準の利用です．しかし，ど ちらも数学的な前提や導出はややこしく，あまり簡単ではあり ません．とくに DIC は「DIC はこのようにおかしい」といった 論文が今でもいろいろと公表されています． できあいのモデル選択基準を使わないモデル選択の方法はいろ いろあります．交叉検証法 (cross validation) などはその代 表といって良いでしょう．
