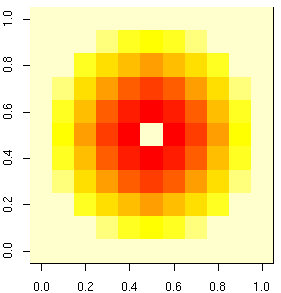
[離散化カーネル]
ここにあげたのは,
その一例.
生態学なんかで使うぶんには,
ちょー精密カーネルなんか必要ないのである
(理由: 阿呆らしいだけだから)
……
しかし,
このように離散化すると,
ますます計算速度が低下するかも.
アルゴリズムに何か工夫が必要だ.

matrix
として表現されてる距離カーネルを,
切り取って,
規格化して,
はりつけるだけだ.
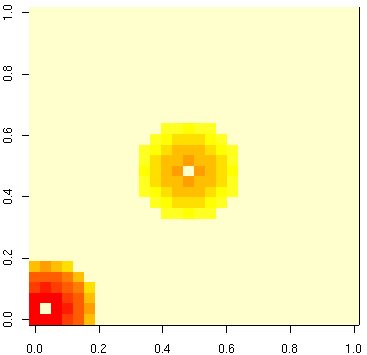
x == 0.0
ぴったりなやつがあった.
これの座標の離散化でしくじっている.
いやはや.
修正.
再転送.
再実行.
時刻は 2045.
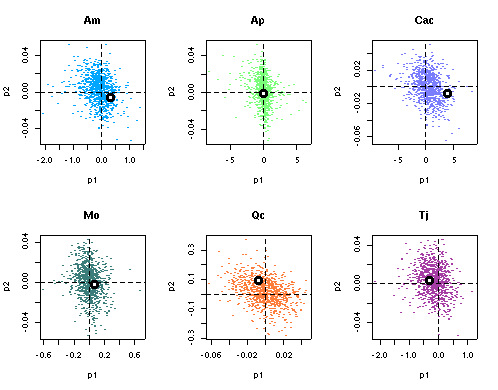
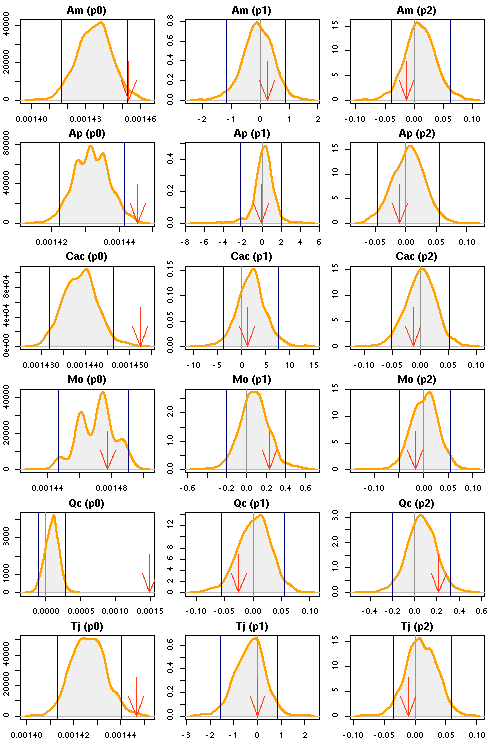

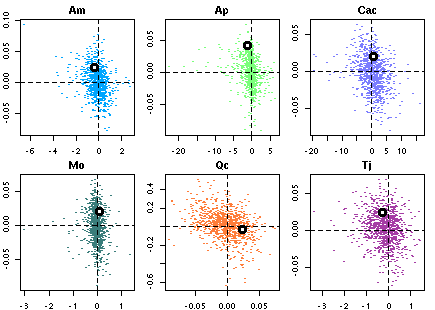
> tapply(d$DBH.cm, d$Sp, function(x) sum(x * x * pi * 0.25)) Am Ap Cac Mk Mo Qc Tj 3426.14 1220.24 942.21 601.10 837.45 38863.24 3959.88ほかならぬミズナラのことだ. こいつだけは「同樹種の大木」に parasitoid を「吸いとられる」 ような推定結果になっている.
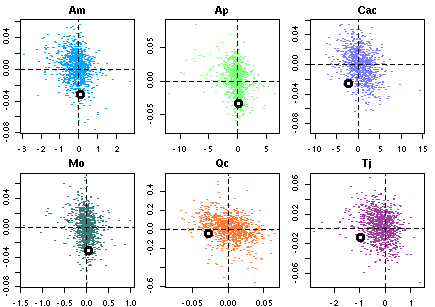
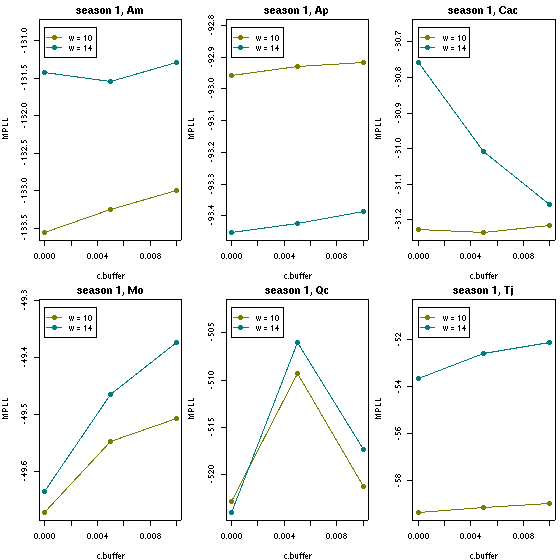
exp(-0.01 * density)
から
exp(-0.02 * density)
と変更してみる.
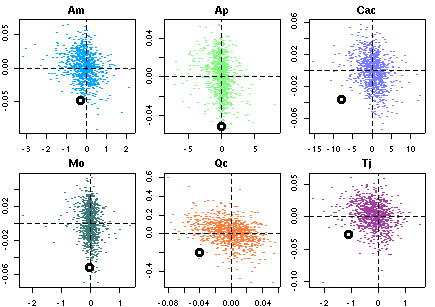
これの具体的な関数型としては f(d) = exp(-0.02 * d) というような密度の減少関数です…… と書いたところで, ちょい失敗をやったことに気づきました. d は現在のところ寄生された host 密度 (樹冠全体推定数) にしてますが, おそらくこれは host 全体にしたほうがマシかもしれません.なる修正の計算結果だが …… 結果がひっくりかえってしまった (しかしこの数時間後にさらにひどい状況になる, それを知るものはまだ人類のだれもが知らないことであった). こんどは apparent competition アリ, の方向ではないか (しかもミズナラ以外は同樹種間の影響が少ない) ……
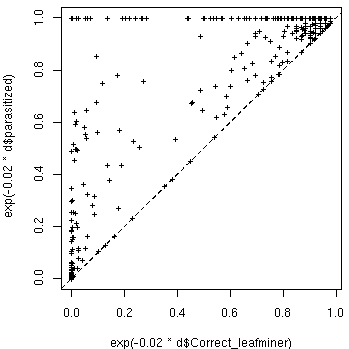
> summary(d$Sp) Am Ap Cac Mk Mo Qc Tj 94 70 68 15 40 163 57が反映されてない, というのが発見の発端だったんだけど. うーむ. 一週間以上きづかなかった. ただちに修正. 計算はゼロからやりなおし …… といっても今まで使いものになりそうな結果が得られていないのは, まあ不幸中のさいわい, とでも理解すればいいのかもしれんが.
try()
で強引に計算してた理由はコレか
……
unless
がない.
しかしながら無限るーぷ repeat
はある.
ということで,
repeat {
density.randomized <- randomization(...)
fit <- glm(...) # MPLE 計算
if (fit$converged == TRUE) break # 終了
cat("ERROR: failure in conversion; retrying ...\n") # やりなおし
}
としてみる.

fit <- glm(...)
として得られた計算結果の fit$iter
すなわち「収束」に必要とした計算回数である.
劣悪なパターンでは (当然のことながら)
fit$iter
が大きい.
fit$iter
の大小をどういう規準で判定すべきか?
これは観測された空間配置で推定させたときの計算回数
fit.obs$iter
を参考にすればよいだろう.
今回はとりあえず
fit.obs$iter + 2
より大であれば,
「収束がおそすぎる」
と判定することにした
(ちょっとキビしすぎるかも).
R
の glm() では
iteratively reweighted least squares (IWLS)
なるよくわからん収束計算方法を使ってるんだけど,
名前から憶測するにおそらくこれは二次収束するからだ.
fit.obs
がうまくできない,
とか.
reject の規準も
fit.obs$iter + 3
より大,
にしてみる.
あまりにも reject 数が多い場合には,
その randomization はヤメということにしたほうがよいのか?
glm()
の計算がうまくいかなかった場合,
converged)
iter)
NA になる
(coefficients)
c.buffer = 0.0).
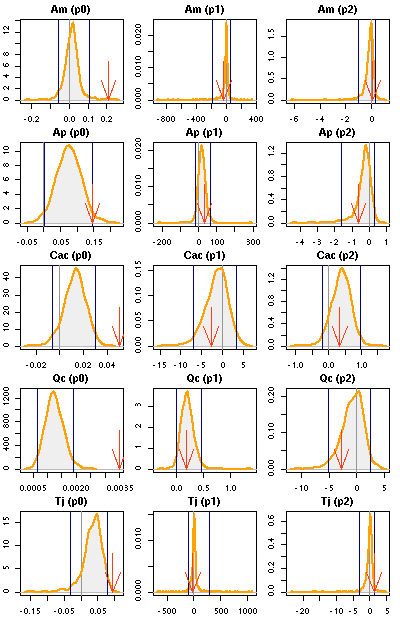
> load("cb0.005/output1.RData")
[1] "results"
> sapply(names(results), function(spc) nrow(results[[spc]]$mple$data))
Am Ap Cac Mo Qc Tj
94 70 68 40 163 57
stepAIC()
なんかはある意味やくにたたん,
というべきか何というか.
まあ,
stepAIC()
は線形モデルの「内部」を探索してくれるもんだからねぇ.
あたりまえのことだけど,
いままで気づいていなかった.
glm()
とかで得られた結果での,
「絶対的な」 (と言っていいのか?)
あてはまりの良さとは residual deviance
であります
(ただし null deviance との比較も必要だろう).

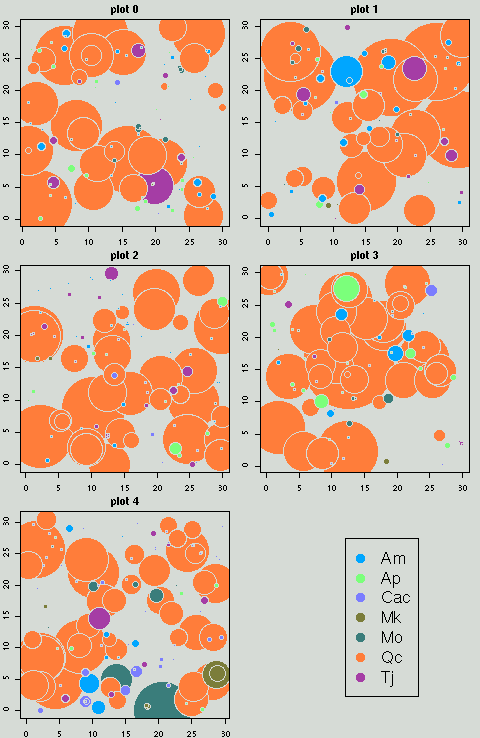
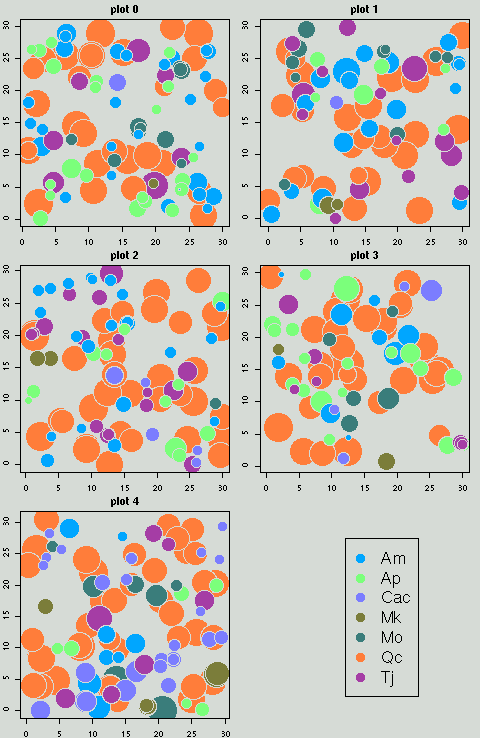
data.frame
化はできた.
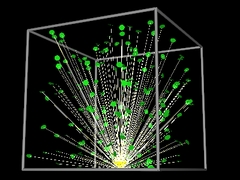
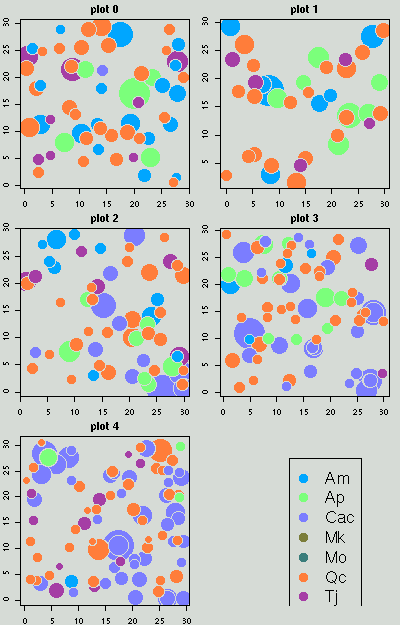
数の増減を視覚化するプログラムを作る.
season3 → 4
は下のよーなかんぢで
(全 season はこちら).
seek.the.nearest <- function(id, x, y)
{
if (length(id) != length(x) | length(x) != length(y))
stop("ERROR: unbalanced vectors of id, x and y")
n <- length(id)
dm <- as.matrix(dist(matrix(c(x, y), n, 2))) # distance matrix
diag(dm) <- NA # to discount self
sapply(1:n, function(i)
id[rank(dm[i,], ties.method = "random") == 1] # RANDOM!
)
}
しかし,
簡潔にかけるからといって読みやすいわけでもない,
と.
計算コストもよくわからん.
実行例:
> seek.the.nearest(c("a", "b", "c"), c(1, 1, 1), c(1, 2, 4))
[1] "b" "a" "b"
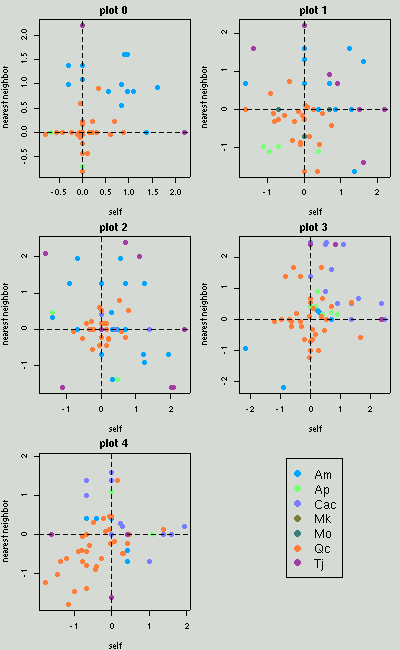
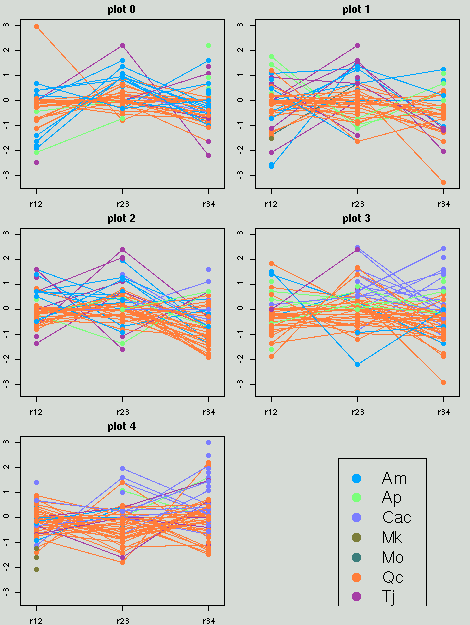
seek.the.nearest()
なる関数を使って,
ある樹木とその最近傍樹木 (同種のみ,または全樹種が選択可能)
における leafminer 数季節変化の「類似性」を図にしてみる.
下の図は
season2 → 3
の同種最近傍との関係である
(全 season はこちら).