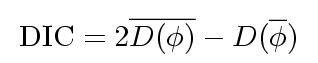
Clark, J.S, Mohan, J., Dietze, M., and Ibanezb, I. 2003. Coexistence: how to identify trophic trade-offs. Ecology 84: 17-31.``Trophic trade-offs'' とかいってるけど, これは Acer rubrum (アメリカハナノキ,カエデのたぐい) と Liriodendron (モクレン科ユリノキ属のたぐい) の局所明るさ vs 高さ成長競争みたいなハナシのようだが.
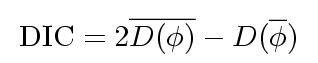
D(φ)
と尤度 L(φ)
の関係を D(φ) = -2 ln(L(φ)) とする.
右辺の第一項は「deviance の事後分布」の平均値を二倍したもの,
第二項はパラメーターの事後分布の平均値を使って計算した deviance
……
まあ,
つまりパラメーター平均値ふきんでのあてはまりがよくても,
周辺尤度の分布があてはまりの悪いところを含んでるモデルはダメ,
ということか.
platex dic.tex
dvips -E -x 3000 -y 3000 dic.dvi -o dic.eps
epsffit ワザ使って
文字を拡大してたんだけど,
それはヤメた)
convert dic.eps dic.png
perl -MDate::Calc -de 0
で interactive interface (debugger) ひらいて,
DB<1> print Date::Calc::Day_of_Year(2005, 3, 27) - Date::Calc::Day_of_Year(2005, 2, 22) 33とすればよいし (あるいは
Date::Calc::Delta_Days() でもよい),
R
で同じようなことをやろうとすれば
> library(chron) # chron package の読みこみ > julian(3, 27, 2005) - julian(2, 22, 2005) [1] 33となる (後期:
difftime(),翌々日に記載).
ということで,
大阪大会
まであと 33 日とわかったので,
私をいつのまにか発表の共著者として登録した
寄生師弟
(これは俗世を捨て人里はなれた山奥で
parasitoid 研究の道にふみこんでる出家とその弟子,
という意味である)
にメイルなど書いてみる.
来週あたり苫小牧出張か?
fitdistr()
を使って,
> x <- c(1, 2, 3, 4)
> fitdistr(x, "normal")
mean sd
2.50000 1.11803
(0.55902) (0.39528)
といったあたりだろう.
さて,
これをもしこういうふうに推定してたら,
> f <- lm(x ~ 1)
> f
Call:
lm(formula = x ~ 1)
Coefficients:
(Intercept)
2.5
「いかがわしいやつ」
と怪しまれることだろう.
しかしながら,
このやりかたにも多少の利点はある.
> logLik(f) `log Lik.' -6.122 (df=2)このようにお手軽に最大化対数尤度を得られる, ということだ.
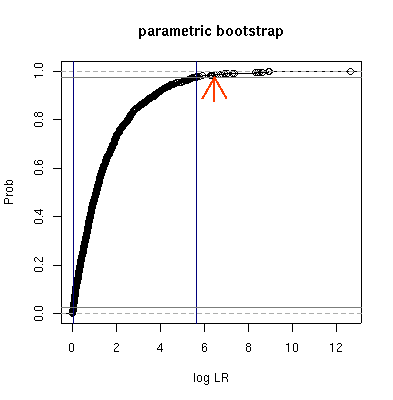
> source("pb.R")
> pb <- pb.lrt.normal(c(1, 1, 2, 2), c(3, 3, 4, 4))
> plot.pb(pb, main = "parametric bootstrap", xlab = "log LR", ylab = "Prob")
difftime("2005-3-27","2005-2-22")
でよい,
とのこと.
うーむ,
知らなかった
……
sa-learn --spam dir
(dir は spam の入ったディレクトリ)
とすればよさそーで.
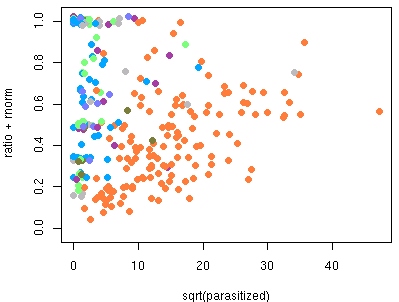
> tapply(d$Samplesize, d$Sp, sum) Am Ap Cac Mk Mo Qc Tj 345 225 123 81 139 3000 180 > tapply(d$N.P, d$Sp, sum) # parasitoid 発生件数 Am Ap Cac Mk Mo Qc Tj 148 91 29 26 57 1072 59わりざん値図など作ってながめてみる.
> M <- sapply(1:3, function(i) c(i, i, i))
> M # 行列
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 1 2 3
[3,] 1 2 3
> v <- c(1, 2, 3) # ヴェクトル
> v * M # ヴェクトルの各要素を各行にかける
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 2 4 6
[3,] 3 6 9
> M * v # 上と同じ
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 2 4 6
[3,] 3 6 9
> t(v * t(M)) # 各列にかけたければ……
[,1] [,2] [,3]
[1,] 1 4 9
[2,] 1 4 9
[3,] 1 4 9
> M %*% v # 内積 (結果は行列に格納されている)
[,1]
[1,] 14
[2,] 14
[3,] 14
> v %*% M # v と列ヴェクトルの内積を並べたもの,というか
[,1] [,2] [,3]
[1,] 6 12 18
t(s * t(W)) %*% d
とすればよい,
とわかった.
ここで
s は species identity vector,
W は距離荷重行列,
d は 宿主 (host) の密度 vector.
> system.time(r <- randomization.tree("Am", d, ldm, n.trial = 1000))
[1] 160.63 0.01 160.64 0.00 0.00
345 個体の 1000 回試行で 160 秒か.
全樹種 100 回試行だと
……
> system.time(sapply(unique(d$Sp), function(spc) randomization.tree(spc, d, ldm, n.trial = 100))) [1] 117.75 0.02 118.01 0.00 0.00二分ぐらいか. ということは 1000 回試行だと 20 分ぐらいだな. これが 4 season で 1.33 時間の, さらに host いれかえ randomization も必要だから …… 必要な予想合計計算時間は 3 時間弱, ぐらいかな. それほど高速化されてない. せいぜい二倍ぐらいのもんか.
> system.time(sapply(unique(d$Sp), function(spc) randomization.host(spc, d, ldm, n.trial = 100))) [1] 166.58 0.00 167.27 0.00 0.00うーむ, やはり試行回数は同じでもこちらのほうが時間かかってしまう. データやりとりを削って overhead を軽くしてみる (が, ぢつは R 内部処理がどうなってるのか, いまいちわからん).
> system.time(sapply(unique(d$Sp), function(spc) randomization.host(spc, d, ldm, n.trial = 100))) [1] 153.01 0.06 153.82 0.00 0.00…… ほんの少しだけ速くなったか. うう.
> system.time(sapply(unique(d$Sp), function(spc) randomization.tree(spc, d, ldm, n.trial = 100))) # trial Ap: [0][100] # trial Qc: [0][100] # trial Am: [0][100] # trial Tj: [0][100] # trial Mo: [0][100] # trial Cac: [0][100] # trial Mk: [0][100] [1] 127.06 0.77 128.02 0.00 0.00ふーむ, さすがに ThinkPad X31 (PentiumM 1.6MHz) よかは速いよね (2.5 分 → 2 分).
save(..., compress = TRUE)
を指定,
少しはちぢんだ.