ぎょーむ日誌 2005-02-23
2005 年 02 月 23 日 (水)
-
0750 起床.
朝飯.
コーヒー.
0930 自宅発.
雪.
0940 研究室着.
-
アカマツりすとらのつづき.
小林さんから光合成論文のほうの Table
作りなおしが提案されてきたんでそっちに取り組んでんだけど,
「ゆーい差」だせとかで鬱々たる気分である.
ゆーい差って,
さかさに振っても全 8 個体しかいないんだが
……
ところで,
人間の
「ごまかし」「いんちき」「邪道な方法」
を創作する能力はまさにこういう瞬間に発動されたりするもので,
私もこの「あまりにも少ない標本数」
というのを逆に悪用できる可能性に気づいた.
つらつらとそのアカマツ観測データ表をみなおしてるうちに,
「8 個体を 4 vs 4 に分割するやりかた」
は 8! / (4! 4!) = 70 とーりしかない.
それだけしかないのであれば,
-
不等分散な状況のもとで
-
「検定統計量」に関する分布を仮定しない
-
最尤推定法
が使えるんでは,
と気づいた.
-
要するに尤度比検定なんだけど,
尤度比の分布に関してなんちゃら近似を導入するのではなく,
70 とーりの尤度比をことごとく算出し,
厳密なる
(そう,無意味に厳密なる)
p-値とやらをつきつけてやろう,
という試みだ.
Fisher の正確確率検定 (FET) の尤度比検定版,
というところだろうか
(ま,
いつものごとくどこかの誰かがすでに考えだしているんだろうけど).
-
さて,
少し冷静に再検討すると
……
このような状況
(標本数がぜつぼー的にたりん)
での尤度比検定わざとして,
parametric bootstrap (PB) 法というのがある,
と以前に粕谷さんから教えていただいたことがある.
PB 法は帰無仮説として推定された確率分布に
標本点集団を生成させる (bootstrap する)
というやりくちである.
ふーむ,
ここらに相違点あるわけで
……
-
FET 的な尤度比検定,
なる考案は
「標本の可能なすべての組みあわせこそが『母集団』である」
という FET 的な発想にもとづいている.
いっぽうで,
PB 尤度比検定は
「帰無仮説 H0 として指定された確率分布が母集団で,
そこから得られる乱数セットが H0 の無作為標本である
(たまたま観測された標本点の組みあわせごときには左右されない)」
ということだよな
……
両者は大標本のもとでは一致するよーな気もするんだが
(ホントか?),
それはともかく,
うーむ
……
現代的な統計モデルの世界では PB の仮定のほうが妥当な気もする.
とくに,
いまの場合,
カウントデータではないんで状態は無限にとりうるわけだし.
-
とゆーことで,
あっさり方針転換して parametric bootstrap でいくことに.
これってやっぱり
R
でやるほうがラクだよな.
しかしアカマツデータは,
Perl でかなり念いりに作ってしまった
(つまり他システムとの協調性をあまり考えてない)
データ管理システムの中に隔離されちゃってるんだよね.
さて.
-
……
と思ったら,
すでに自分で「データとりだし用 Perl スクリプト」
は構築していた
……
しかも一年以上前に!
これをさらに
昨年 5 月 17 日ごろ
にも改良してるよーだ.
いやはや,
こんなに長びかせてはいけませんなぁ.
-
昼飯.
けっこう雪ふってる.
-
アカマツりすとらの続き.
さて,
データとりだしスクリプトが見つかったのはいいんだが
……
さて,
parametric bootstrap 尤度比検定と自動作表をどう融合させればいいのか?
-
といったムズかしい問題に懊悩するのはヤメて,
とりあえずあとさき考えずに PB 問題に取り組むことに.
-
あるデータがあったときに,
R を使ってこれに正規分布 (あるいはいろいろな確率分布)
をあてはめるにはどうしたらよいか?
たぶんまっとうな答えは,
MASS package の
fitdistr()
を使って,
> x <- c(1, 2, 3, 4)
> fitdistr(x, "normal")
mean sd
2.50000 1.11803
(0.55902) (0.39528)
といったあたりだろう.
さて,
これをもしこういうふうに推定してたら,
> f <- lm(x ~ 1)
> f
Call:
lm(formula = x ~ 1)
Coefficients:
(Intercept)
2.5
「いかがわしいやつ」
と怪しまれることだろう.
しかしながら,
このやりかたにも多少の利点はある.
> logLik(f)
`log Lik.' -6.122 (df=2)
このようにお手軽に最大化対数尤度を得られる,
ということだ.
-
「にわか Unix server 管理者」
を押しつけられた小林さんより緊急お電話 help
が.
苦闘しておられるよーで
……
-
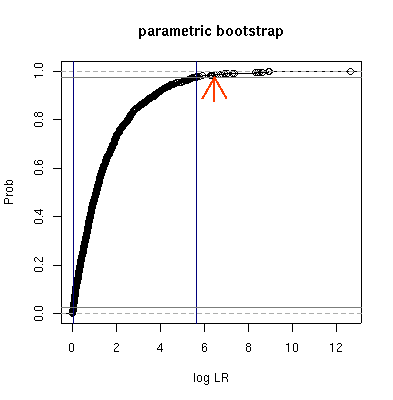
セミナー前にひととーり parametric bootstrap
尤度比検定の関数定義ファイル
pb.R
かけた
(後記: このプログラムではまだ十分に
「不等分散」な状況をあつかえていない).
動作はこういうかんぢで
(計算時間: 試行回数 1000 で 12-13 秒ぐらい, ThinkPad X31):
> source("pb.R")
> pb <- pb.lrt.normal(c(1, 1, 2, 2), c(3, 3, 4, 4))
> plot.pb(pb, main = "parametric bootstrap", xlab = "log LR", ylab = "Prob")
-
1630 より本年度最後の
Trendy セミナー,
本日は道立林試の真坂さん,
シラカンバとか風媒花の性配分について.
現象はすごくおもしろいが,
こういう
「もってる資源量ことなる個体たち」
の正面激突闘争のゲイム理論的なとりあつかいは難しい
(金もちが勝つにきまってるから).
で,
それを計算できるよーにしようとすると,
いろいろとヘンなことになる,
とわかった.
-
お茶部屋でいろいろ話してから
1930 研究室発.
吹雪.
JR 札幌駅北口で本日の講演者を囲む懇親会.
大学院生たちと道立林試のハナシなどなどいろいろとうかがう.
2250 帰宅.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0830):
米麦 0.7 合.
ジャガイモ・タマネギ・ニンジン・海藻・煮干の味噌汁.
- 昼 (1310):
研究室お茶部屋.
米麦 0.8 合.
ジャガイモ・タマネギ・ニンジン・海藻・煮干の味噌汁.
- 晩 (1940):
JR 札幌駅北口の居酒屋
「うみぼうず」
でいろいろと.