ぎょーむ日誌 2006-10-29

2006 年 10 月 29 日 (日)

• 0730 起床． 朝飯． コーヒー． 怠業．
• 昨日から， というかここしばらくひっかかっているのは， 10/20 にやった「明るさ」なる計算なんだよね (下の図はそのときに志水さんデータをつかって R で作図したもの)． これは夏至の日の南中時刻のひあたりを相対値化したものである．

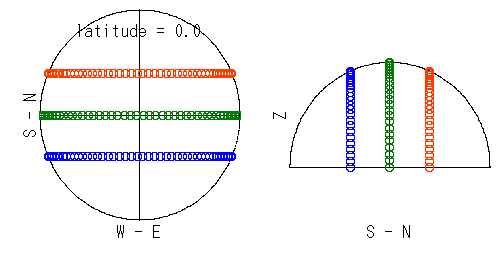
[大雪山主稜線上の地衣類]

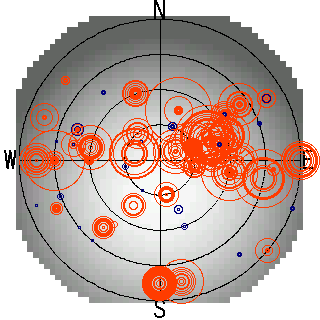
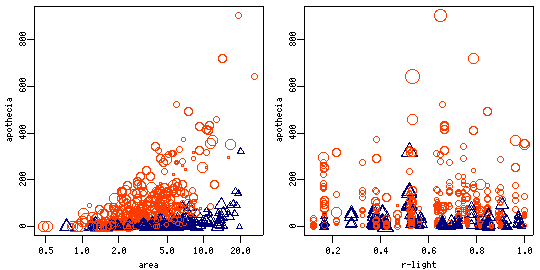
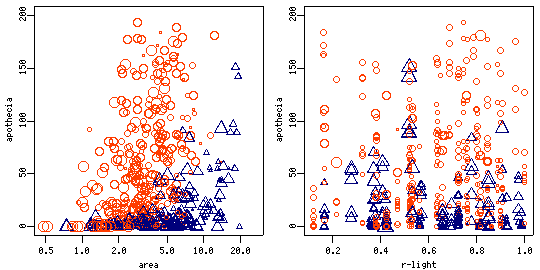
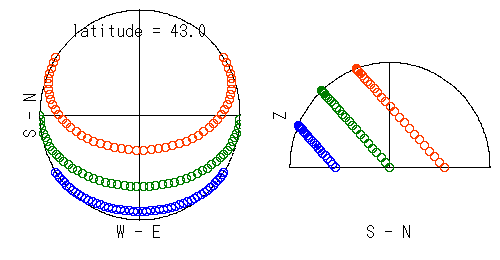
…… が好む岩面? 志水さんデータを使った作図． 北緯 43° において日当たりが悪いところはダメそう． しかしながら， 日当たり良すぎるところもやはり ……

• まあ， これで太陽をくるくるまわしたところで， あまり上の図は変わらないだろう， とは思うわけだが ……
• で， この「明るさ」と呪われ割り算値で表現されてる繁殖努力の関係はこう， と．

[呪われ割り算値]

ディスプレイ上で作図してすぐに消去する場合は 「うん? ユルい相関?」 とかいいかげんな感想もつばかりだけど， こうやってじっくり見ていると， 次第にいろいろ気になってくるわけで ……

• やっぱりこういうカウントデータを割り算値化するのは ぢつにバカげた所業ですね， ということで志水さんの元データを使って図を作りなおす． やはりこちらのほうがずっと安心感がある．

• 上の図でわかることは， 私がてきとーに三次元計算してみせた 「明るさ」とやらは繁殖努力とあまり関係なく， やはり個体サイズそのもののほうがよっぽど支配的である， ということだ． そしてこの overdispersion は random effects の大きさを表現している．
• apothecia 数 200 以下の部分だけを図にすると， こうなる． そうすると今度はナリはでかくてもあまり繁殖してないやつがいるわけで …… これは何か「明るさ」とやらで説明できるのか? それとも「人間の知ることができる限界」こと random effects の嵐の中にかき消されてしまうのか?

• 1020 自宅発北大構内走． 使うかどうかはともかく， 走りつつアタマの中で球面座標系を設定して， そこで太陽を動かしてみる． 「夏至の日の日の出から日没まで何時間か?」 といった問題を考えるときは， 「天動説」的に不動の大地から見あげた 天球上に太陽の軌道を設定してやると考えやすい …… 「地球は自転してるから」 とか考えるとわけわからなくなりがちである． そしてその世界の「外側」の 「東/西」にたってながめ， 次に「北」からながめれば， どうやって昼間時間を計算すればよいかわかる， と．

[天動説世界]

ぎょーむ日誌 2001-01-15 から． これは「外側」の「西」から見た図．

• 1120 帰宅． 体重 72.2kg． 昼飯．
• 1315 自宅発． 晴． 1330 研究室着．
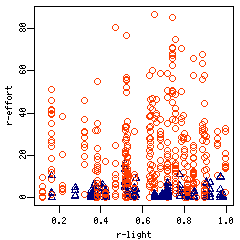
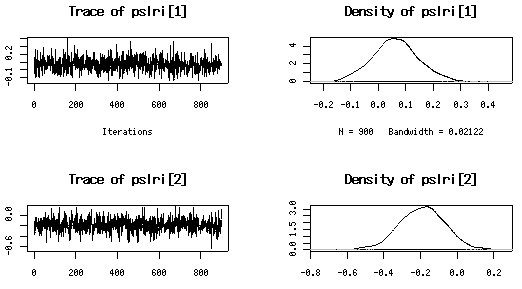
• 昨晩帰るまえに R2WinBUGS に命じておいた， n.burnin = 30000, n.iter = 60000 のトリプル MCMC 計算はとっくにオワってるわけで …… 計算時間はおよそ 5000 秒だったか． きれいに収束している． そして fixed な「明るさ」 (今回は logit 変換) のパラメーターの事後分布に関しては， まあゼロにひっかかる「妥当な」結果ともうしますか．

• 「モデルの改善にはならんだろうなあ」 と思いつつも， 太陽問題をひねくってみる． 休日の娯楽， ということで． R で度数法から弧度法 (ラディアン) に変換する関数を準備しといて，

  	rad <- function(a) a / 180 * pi
  

  下のように計算すれば昼間の長さがわかる．

  	(1.0 - acos(tan(rad(A)) * tan(rad(N))) / pi) * 24
  

  たとえば， 札幌あたり (N <- 43) の夏至のころ (A <- 23.4) だとこの計算だと「昼間」の長さ 15 時間 10 分になる (これは太陽の「中心」が地平線からでて沈むまで)． ただし， 実際の日の出・日のいりの定義は 「太陽のはしが出入りする時刻」 になるからこれとは異なり， 国立天文台のペイジ とかでわかるんだけど， 15 時間 23 分である (同様に， ここでみると春分・秋分の日の昼間の長さも 12 時間ではなく， 12 時間 11 分ぐらいである)．
• …… と思ったら， Wikipedia の 解説 (あるいは国立天文台の FAQ 3-3) によると， 太陽の大きさによるずれはそれほどでもなくて， むしろ大気の屈折とかによるずれのほうが大きいようで． で， そのずれは場所 (緯度) によって異なるわけね．
• そして日曜日のお茶部屋も「食」をめぐるキビしい闘争が …… 私など何の関係もない傍観者なのに可及的すみやかに逃げださざるをえなかった．
• 夜までかかって天球上の太陽軌道を描く R プログラムかく． てこずったのは， (北海道における植物生態学研究にはほとんど役にたたぬ) 秋分 - 冬至 - 春分の軌道の計算で …… 「回転」させるべき角度の計算をいろいろかんちがいしてたもんで． 北緯 43 度はこのあたりの緯度．

• 上の軌道とこの下の図をみくらべると， 意外と夏至の日ってのは北側からも ……

• 本日は (娯楽的な) 太陽軌道の計算だけ． 「明るさ」計算の再検討はまた明日以降， とゆーことで． 2000 研究室発． 2015 帰宅． 晩飯．
• 輪読会の予習．
• [今日の運動]
  • 北大構内走 60 分間．
• [今日の食卓]
  • 朝 (0800): バゲット．
  • 昼 (1200): うどん． ニラ卵．
  • 晩 (2110): 米麦 0.7 合． チンゲンサイ・ネギ・ショウガ・エノキダケ・豆腐のスープ．