ぎょーむ日誌 2005-05-15

2005 年 05 月 15 日 (日)

• 1010 起床． 朝飯． コーヒー． 洗濯． 怠業．
• かなりの雨降り． 北大構内走やめとくか．
• 1610 自宅発． 雨． 1630 研究室着．
• またしても「カクレ」状態問題の検討に没頭してしまう …… というか， 先月末からこの問題の周辺に アタマがとらわれてしまっているんだけど． いやはや， ぢつはこれもまた一種の怠業の形態にほかならないのかも ……

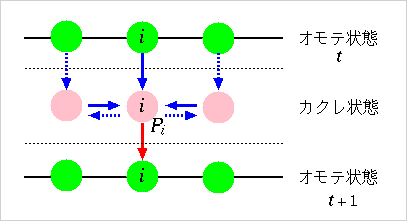
• 先日， auto-logistic model と Ising model の対応がよーやくにして理解できてしまった． この対応づけについて考えていくと， 今度はカクレ状態を生成する Gibbs sampler の定式化が気になってくるわけで …… これまでは， 上の図に実線矢印 (青) でしめされてる効果を勘案して 線形予測子 (linear predictor) を構成し， それでもってカクレ状態 i をきめればよい， と考えていた．
• Gibbs 分布からの標本を生成するためだけのシミュレイション (forward 過程の Gibbs sampler とでもいうべきか) ならば， おそらくそれでいいんだろう， という気がする．
• しかしながら， パラメーター推定 (inverse 過程) に関してはどうか? Gibbs sampler はオモテ状態 (t) とカクレ状態だけでなく， オモテ状態 (t+1) も考慮すべきではなかろうか， というあたりでつまずいているわけで ……
• 同じモデルに関して， forward/inverse 二種類の Gibbs sampler が必要なのかしらん? だとすると面倒だな， などとアヤしみつつ検討をすすめてみる．
• そしてここで興味ぶかいのは， 「オモテ状態 (t+1) も影響するはず」 という考えが正しいとすると， カクレ状態 i を決める状態遷移確率は オモテ状態 (t+1) の i の関数ではなく， むしろ「i の近傍」のオモテ状態 (t+1) だと考えるべきなんだよね． 上の図の水平な破線矢印 (青) が示すようにカクレ状態 i はその「近傍」に影響をおよぼすからだ (というのも， カクレ状態 i がオモテ状態 (t+1) の i には影響しない， と考えないと尤度方程式が構成ができないだろう， というのがこの推定の重要な部分なんで)．
• なんだかよくわからぬまま撤退． 2035 研究室発． 2050 帰宅． 晩飯．
• カクレなハナシのつづき．
  • 推定のための Gibbs sampler はオモテ状態 (t+1) からも影響をうける
  • そのときに場所 i に影響をおよぼすオモテ状態 (t+1) は「i の近傍」の状態である
  という考えが正しければ， カクレ状態 i の状態遷移確率はどう書けるのだろうか? これは先日あきらかになった Ising model との対応から導出できるはずで …… やってみると， どうも形式的には logistic 的な関数となっているなぁ．
• これって正しいのか?
• どういう Gibbs sampler が必要か， という問題は推定方式に依存するのか?
  • EM アルゴリズムで期待対数尤度最大化するなら 素朴な Gibbs sampler でよい
  • Bayesian inference の場合は オモテ状態 (t+1) まで考慮した Gibbs sampler が必要である
  …… うーん， どうなんでしょね．
• [今日の運動]
  • いやはや運動休養日
• [今日の食卓]
  • 朝 (1040): 米麦 0.6 合． キュウリ． サケの電磁波蒸し． 炊飯器はいぜんとしてコワれているので， 鍋炊飯生活が続いている．
  • 昼 (1410): 米麦 0.6 合． ニンニクの茎・卵の炒めもの． ワカメスープ．
  • 晩 (2200): 米麦 0.8 合． キュウリ． キャベツ・ブナシメジのシチュー．