ぎょーむ日誌 2009-12-12

2009 年 12 月 12 日 (土)

• 0830 起床． 朝飯． コーヒー． 怠業．
• 昼飯． 1340 自宅発． 曇． 1400 研究室着．
• 岩波本作業， GLM あれこれをつめこむ第 3 章， 今日は family = Gamma の例題づくり．
• R の glm(y ~ x, family = Gamma(link = "log")) な GLM は今までよく理解してない面があったんだけど， 今回よーやくにして分散まわりのあつかいがわかった．
• glm(y ~ x, family = Gamma...) の場合， link = "log" が使いやすい． カノニカル link 関数 μ = -1 / z はなんとも理解しにくいので． link = "log" の場合， 平均値は exp(線形予測子) となる． 他の glm() と同じく， 線形予測子の係数が最尤推定される．
• さて， ここがややこしいのだけど， もいっこパラメーターが推定されて， これは dispersion parameter というものだ (glm(y ~ x, family = gaussian) の場合も同じパラメーターが推定される)． summary(glm(...)) すると算出される．

Call:
glm(formula = y ~ log(x), family = Gamma(link = "log"), data = d)
(略)
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.04032    0.11877  -8.759 1.61e-11
log(x)       0.68325    0.06838   9.992 2.60e-13
---

(Dispersion parameter for Gamma family taken to be 0.3250858)
(略)

• この dispersion parameter を θ とすると， 推定されたガンマ分布は
  • 平均 = exp(線形予測子)
  • 分散 = θ × 平均²
  となる． R の glm(y ~ x, family = Gamma...) の分散関数は mu^2 である， ってのはこーゆー意味だったんだね ……
• さてさて …… いっぽうで， R のガンマ分布 のパラメーター指定は， たとえば密度関数だと dgamma(x, shape, rate, ...) なので平均は shape / rate 分散は shape / rate / rate となる．
• したがって， さきほどのように平均・分散が推定できたら， shape と rate は以下のように算出できます， と．
  • rate = 平均 / 分散 × θ
  • shape = 平均 × rate
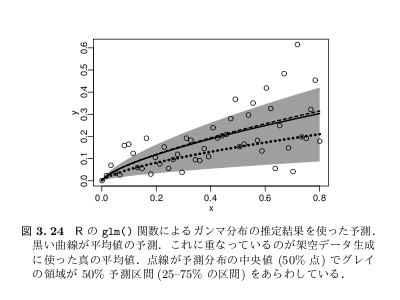
  …… といったことを理解しておけば， 以下のような作図ができます， と．

• このようなことを説明できる 例題 & 作図とかはできたけど文章のほうはあまり進捗しないまま終了 …… 2000 研究室発． 2020 帰宅． 晩飯．
• [今日の運動]
  • うんどう休養日， つづく．
• [今日の食卓]
  • 朝 (0900): イソップベイカリーのクロワッサンとか．
  • 昼 (1300): スパゲッティー． ボロネーゼ．
  • 晩 (2100): 米麦 0.8 合． 油揚・タマネギの味噌汁． チンゲンサイ・豚肉の炒めもの． ヨーグルト．