ぎょーむ日誌 2007-07-24

2007 年 07 月 24 日 (火)

• 0700 起床． コーヒー． 朝飯． う， 朝からカウントデータ解析こんさる …… 1035 自宅発． 自宅発． 1050 研究室着．
• えーと昨日かいてたアリ neural network で 炭化水素濃度を対数変換して使うことの正当化のひとつは， 「感覚の強さは刺激の強さの対数に比例する」 という フェヒナーの法則 (wikipedia: Weber-Fechner law) の悪用， ということで．
• 今のデータにはゼロデータは含まれていないけど …… もし (もとデータもっておられる) 城所さんからゼロを含むデータ (つまり「ゼロぬき処理」する前のデータ) を渡された場合は， そうだなあ， 測定誤差とかを考慮した Bayesian なあつかいが必要になるのかな? まあ， 最終的には (ある刺激閾値をこえる入力にしか応答しない) 非線形な neural network に「食わせる」わけだから， 濃度 0.0000001 μmol (?) とかてきとーな値をおしこんでもいいわけだが …… そうか， 線形判別法とかと比較したときのニューラルネット判別の強みのひとつは， こういう問題をうまくあつかえる， ということだな．
• 昨日の library(nnet) による炭化水素データ解析のつづき， じつは同 package の multinom() (多項 logistic 回帰) でも同様に推定できるとわかった．

> fit0 <- multinom(colony ~ ., data = dlog)
> fit0
all:
multinom(formula = colony ~ ., data = dlog)

Coefficients:
         (Intercept)       A       B         C        D         E        F        G
Hoshioki    -160.787  93.495  155.25 -347.8654  -22.081 -194.3546   74.185 -169.080
Ishikari     -20.039 -63.042 -244.37 -403.2446 -371.311  -77.1832  526.722  279.371
Jozankei    -133.633 168.490 -200.43   68.1970 -314.438 -261.4539 -167.454  -42.431
Oshoro       193.391 -16.787 -116.28    6.6953   21.332 -254.0034 -313.117   88.331
Shinkawa     -25.612 120.607  173.06 -110.2501   57.424    3.5852 -263.726  -57.633
Tarukawa    -146.064 -23.492 -267.25  -82.8609  249.269  -61.7068  214.712 -147.946
                H         I        J        K          L        M       N       O
Hoshioki    7.670  388.5743  -3.9029 -304.827 -233.90818  616.454 192.311 -12.395
Ishikari -151.814 -491.3550 301.3444  -41.869  345.57834  126.962 -58.226 115.736
Jozankei  447.592    3.2086  60.5417  -74.409 -148.12248   89.806 258.123 131.966
Oshoro    -98.285  223.2290 159.5395  187.517   -0.19016  329.265 166.029  78.323
Shinkawa -205.379   74.1548 -19.9271  184.362  276.70534 -101.728  29.297 -67.805
Tarukawa  -85.172 -256.0845  40.4551  328.460  -50.73650   48.469 138.853 -79.403
                P         Q        R        S         T       U         V         W
Hoshioki  186.531  116.7819  -13.252 -203.153  -90.1263  125.86 -252.2161 -111.3959
Ishikari  216.796    1.2474  111.223  216.794  104.7930 -229.66  147.5471   -4.2782
Jozankei   43.812 -181.9078 -118.064  216.945  336.6963 -162.95   67.4382   40.3054
Oshoro   -185.117   50.8535   36.150 -200.943 -135.1985  224.57 -155.1527 -198.7463
Shinkawa -104.847    9.7351  378.913   22.425   62.7400  293.75 -308.1354   -9.0895
Tarukawa    4.112  308.4419  311.307 -175.804    9.7507 -172.23    3.0234  -91.7194
                X        Y
Hoshioki   58.695  -47.898
Ishikari -187.447 -213.472
Jozankei  -60.082 -128.031
Oshoro     15.324  -16.013
Shinkawa -415.227  -11.925
Tarukawa   21.964 -204.938

Residual Deviance: 2.7726 
AIC: 314.77 

• しかも (なンと!) stepAIC() によるモデル選択までできる， と． 25 箇所のガスクロマトグラフィーによる ピークのうち判別に使える部分を 「選んで」いる， という ……

> stepAIC(fit0)
...
Call:
multinom(formula = colony ~ D + G + K + M + N + O + P + Q + R + 
    S + U + V + W, data = dlog)

Coefficients:
         (Intercept)        D        G        K     M     N        O         P        Q
Hoshioki    -35802.0   4378.6 -20031.6 -30456.7 58773 20507  -1527.9  -4944.70   9888.7
Ishikari     -5264.0 -59267.7  51292.0 -17213.2 15649 33978  10244.8   -282.82 -15747.8
Jozankei      1298.8 -48528.5  28208.0  -5714.3 33506 32659   6243.7 -19584.80 -18697.0
Oshoro       30241.9  -9374.9  -5951.1 -10068.7 31545 26913   9651.4 -11372.27   4636.0
Shinkawa    -25116.1   9907.5  -7978.4  -7677.5 19680 14561 -12884.9  -4997.35  17466.9
Tarukawa    -15535.1  20752.2 -40435.8   7213.4 13204 13532 -16695.3   8848.42  23986.5
               R        S          U         V      W
Hoshioki 22094.6 -19065.5  34809.459 -48162.57 -24981
Ishikari -3067.5  12265.3     94.521  -7033.05 -15551
Jozankei  8837.3  -2067.4   7410.352  -3107.35 -15260
Oshoro    1107.5 -16335.5   2408.336  -5926.06 -19343
Shinkawa 49170.6 -36876.6  32909.337 -58468.25 -16706
Tarukawa 23580.8 -22431.6 -12271.873   -489.45 -13283

Residual Deviance: 2.7726 
AIC: 170.77 

• multinom() のコードみてみると 内部で nnet( ..., skip = T, size = 0, ...) つまり中間層 (隠れ層) の個数をゼロにして入力層と出力層を直結している (skip-layer connection)， とわかった． モデル選択する前後でどちらも「正答」率 95% 以上 (ということで Residual Deviance がだいたい同じ値になっている)．
• まあ， これまた昨日と同じく， 「現実のアリにとってはありえない学習」 となるわけだが．
• このあたりのこと勉強するには， たとえば library(nnet) まわりを解説している MASS4 本 がとうぜんながら有用である．
• てなことばかり， で昼飯．
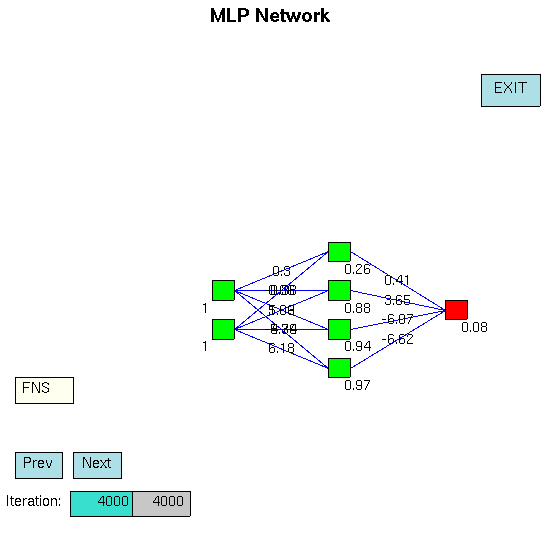
• 昨日 library(nnet) の nnet() のことを「パーセプトロン」と書いたけど， Ripley 先生の説明よんでるうちにこれって (一番単純な) パーセプトロンではない， という気がしてきた． そのあたりを検証してみる実験． (隠れ層-出力層間の結線加重だけを調節する) パーセプトロンが苦手とする XOR 問題 をとかせてみる．

  > (d <- data.frame(z = c(0, 1, 1, 0), x = c(0, 0, 1, 1), y = c(0, 1, 0, 1)))
    z x y
  1 0 0 0
  2 1 0 1
  3 1 1 0
  4 0 1 1
  > nn <- nnet(z ~ x + y, data = d, size = 4)
  # weights:  17
  initial  value 1.130982 
  ...
  final  value 0.000059 
  converged
  
  > nn$fitted.value
          [,1]
  1 0.00021232
  2 0.99940975
  3 0.99235554
  4 0.00076111
  

  …… うまく学習してるぢゃん． ということで隠れ層-出力層間の結線加重だけを調節する パーセプトロンではない， と示された． とはいえ， バックプロパゲイション使ってるわけでもないし． ?nnet によれば optim( ..., method = "BFGS") 使ってるらしい．
• まあ， ただ単に「feedforward 型の三層ニューラルネット」と言えばいいのかな? あるいは私のパーセプトロン定義がまちがってて， これも nnet() も単なる多層パーセプトロンと考えればよいのかな?
• ともあれ， nnet() はかなり難しい問題もあつかいうる， とわかった． なかなかすばらしいですね．
• R には library(neural) ってのもあるなあ …… こういうヘンな GUI つき．

• 他にも library(AMORE) ってのもあるんだけど， なんだかこれはややこしい ……
• エゾアカヤマアリ体表面炭化水素組成の ガスクロマトグラフィーデータについて， 神戸大の城所さんからメイルでいろいろと教えていただいたので， 今後のこのあたりの方向なども検討するため， ちょっと時間をかけて返信かき．
• そしてアリ文献よみをほうりだして， アリ炭化水素データの library(nnet) による学習 & 試験をくりかえした結果， 「とりあえず， まあ， 沖縄発表はコレで OK だろ」 な結果が得られた …… えーと正確に言えば， もうちょい定量的にやる必要あるんだけど， 基本アイデアはおそらくまちがっていない， という見とおしが得られた．
• 調べたいことはコレ．
  • 石狩浜 ``supercolony'' (SC) 内の Hoshioki colony のアリは SC 内の他コロニーのアリに比較的寛容， のんびりしてる
  • それに対して SC 外の Jozankei colony のアリは凶暴， 他巣のアリにひたすらかみつきまくり
  同じエゾアカヤマアリなのに， どうしてこうも違うのか?
• で， 考えてる理由は簡単で
  • Hoshioki colony のアリが他の生物個体に出会うとすれば， それは同 colony のアリである確率が高い (石狩 ``supercolony'' 内はエゾアカヤマアリが高密度)
  • Jozankei colony のアリが他の生物個体に出会うとすれば， それは他種の生物である確率が高い (Jozankei はエゾアカヤマアリ密度が低い)
  こういうそれぞれの環境で敵・味方の炭化水素パターンを 「学習」しつつ暮らしていると， Hoshioki では同種のアリに対する判定が甘くなり， Jozankei では厳しくなるだろう， と．
• つまり 「訓練用データ」の中にしめる「敵」の分量が少なければ， 炭化水素パターンを判定する神経回路網の 「同種」に対する判定が甘くなるように訓練されてしまうだろう， と．
• まあ， 論文化するときには， いろいろなセットで調べつくさないといけないんだろうけど …… とりあえず， 本日準備した「訓練用データ」は
  • mate (味方): Hoshioki コロニー 10 個体ぶんのデータの各 25 ピークに「ちょっとだけ」正規乱数でゴミを 追加した「ニセ」 Hoshioki アリデータ
  • enemy (敵): mate と同じように作るんだけど， もっと正規乱数ゴミが大きい (乱れたパターン)
  これを合計 200 個体ぶん準備する， と．
• 試験は実際のアリデータを使う
  • same.nest: Hoshioki colony の 10 個体， つまり Hoshioki アリからみて同巣のアリ
  • diff.nest: 石狩浜 supercolony の他の 3 巣 の 30 個体
  • non.sc: 石狩浜 supercolony 外の 3 巣 の 30 個体
• まず， 訓練用データを mate : enemy = 180 : 20 でやった場合， つまり石狩浜的な状況． これは一例にすぎないんだけど， たとえばこういう結果がよく出る．

  # 訓練の結果
          enemy mate
    enemy    20    0
    mate      0  180
             
  # 試験
              enemy mate
    same.nest     0   10
    diff.nest     0   30
    non.sc        1   29
  

  つまり他巣・SC 外のアリをみても mate だと思ってしまう， と．
• つぎに 訓練用データを mate : enemy = 100 : 100 でやった場合， つまり (いわば) Jozankei な状況． これも一例にすぎないんだけど ……

  # 訓練の結果
          enemy mate
    enemy   100    0
    mate      0  100
             
  # 試験
              enemy mate
    same.nest     0   10
    diff.nest    11   19
    non.sc       12   18
  

  つまり他巣・SC 外のアリをみたときに enemy だと判定する確率が高くなるんでは， と．
• まあ， これは訓練用データのばらつきその他のせいで， にゅーらるねっとアリにも個性がでてしまうので， replication をいくつもとって敵性判定の確率の確率分布なんかを 生成しなければならない …… とはいえ， 訓練データの偏りぐあい (enemy が多いか少ないか) で「判定の甘い辛い」は変わるだろう， と．
• この実験で再現できてないのは， SC 内 (diff.nest) と外 (non.sc) がまったく区別できてない， ということだ． このあたりは城所さん秘蔵 (?) データを使うとよいのかもしれませんなぁ …… まあ， こんなのは「沖縄」後でもよさそうだし．
• ちまちまと いろいろな実験やってみたんだが …… enemy をもっとでたらめなパターンにすると， enemy に包囲された状況であっても 「エゾアカヤマアリなら誰でもトモダチさ!」 となってしまうようで．
• これで沖縄発表の空想的な要旨に書いたコトはだいたい実現したので， ひと安心． 脱力． 明日ひととーり反復シミュレイションをかたづけてしまおう． 2035 研究室発． 2050 帰宅． 体重 67.0 kg． 晩飯の準備． 今日のうんどう …… にとりかかるのにすごく時間かかる． 晩飯．
• 査読依頼がきたんだけど， 要旨をながめるに， 本文を読んだら「ぜんぶやりなおし」 とかいう誰にとっても楽しくも嬉しくもない 長文の査読報告かかねばならぬ予感をはらんだモノだったので， 別の犠牲者を選んで decline to review 書く．

  Unfortunately, I am not familiar with the XXX methods used in the paper at all. I would suggest that Dr. XXX (xxx@xxx.ac.jp) is one of the experts at the ...

• [今日の運動]
  • 腹筋運動 30 × 3 回． 腕立ふせ 10 × 3 回． スクワット 100 回．
• [今日の食卓]
  • 朝 (0840): 米麦 0.5 合． ネギ・豆腐の味噌汁． タマネギ・ニンジン・レタス・ピーマン・ショウガ・ニンニク・ ブナピー・ホタテの炒めもの． トマト．
  • 昼 (1310): 研究室お茶部屋． 納豆巻． 野菜ジュース．
  • 晩 (2310): 米麦 0.8 合． トマト． キャベツ・ニンジン・タマネギ・バジルのサラダ． モヤシ・ネギ・豆腐・卵の炒めもの．