
dmnorm()
の事前分布と逆 Wihart 分布 dwish()
によるちょー事前分布を使ったモノになる,
と.
vector valued relation betaS must involve consecutive elements of variable
……
これはけっこうばかげたもので,
for (j in 1:N.sp) {
betaS[1:N.betaS, j] ~ dmnorm(V.zero[], inv.vc[,])
}
inv.vc[1:N.betaS, 1:N.betaS] ~ dwish(R[,], Deg.freedom)
とゆー書きかたは許されないけれど,
for (j in 1:N.sp) {
betaS[j, 1:N.betaS] ~ dmnorm(V.zero[], inv.vc[,])
}
inv.vc[1:N.betaS, 1:N.betaS] ~ dwish(R[,], Deg.freedom)
なら OK ゆー意味だと判明した.
やれやれ.
これって C 言語とか使ったことあるヒトじゃないと,
自力では発見不可能ではないかな?
R = diag(rep(1, 3), 3)
や
R = diag(rep(2, 3), 3)
ではなかなか収束しなかった.
R = diag(rep(0.5, 3), 3)
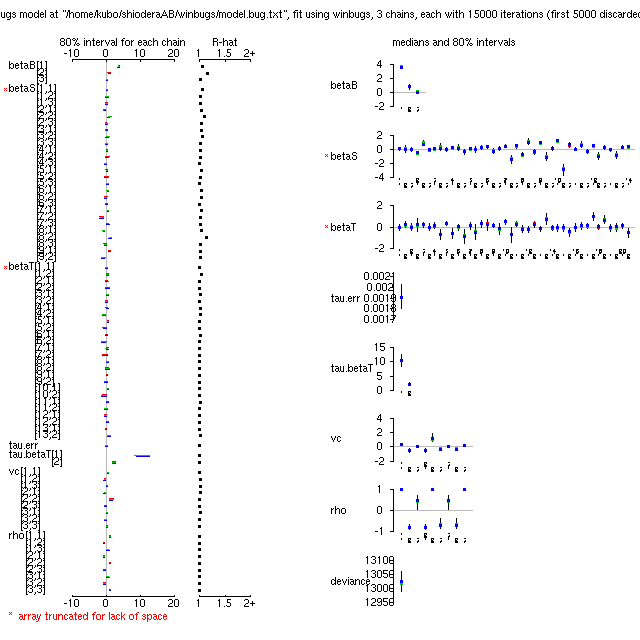
として全 15000 MCMC step (burn in = 5000)
とすると MCMC 計算に 1111 秒を費やして
……
キましたねえ,
どーやらうまくいったようだ
(事後分布表,
BUGS code).
save(post.bugs, file = "...")
と保存して,
ついでに久保バックアップ網のあちこちに保存.
脱力.
脱力してる場合ではないんだけど,
こういう計算ばかりでばてますなぁ
……
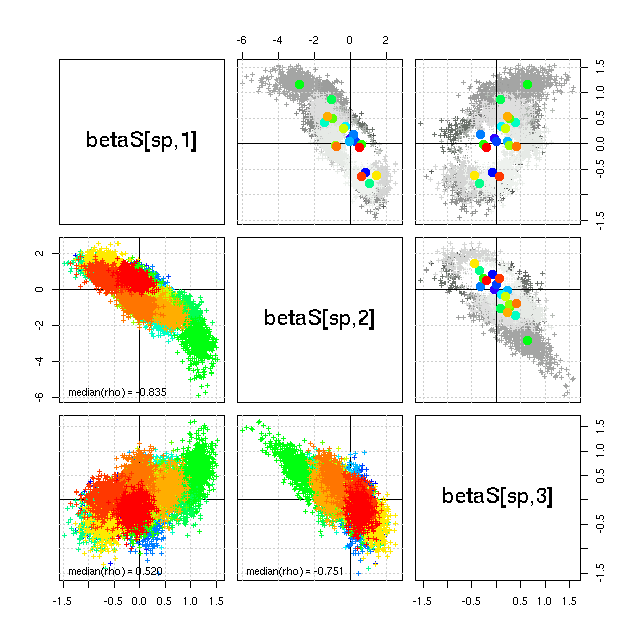
> median(post.mat[, "rho[1,2]"]) [1] -0.7936 > median(post.mat[, "rho[2,3]"]) [1] -0.6687 > median(post.mat[, "rho[3,1]"]) [1] 0.4464事後分布の相関係数を計算する関数を作って計算させてみると,
median(rho[1,2]) = -0.835 median(rho[2,3]) = -0.751 median(rho[3,1]) = 0.520なンと言うべきかよくわからないけど, 事前分布にくらべて事後分布は「相関が強まる」のかしらん? コレってあたりまえのことなのかな?
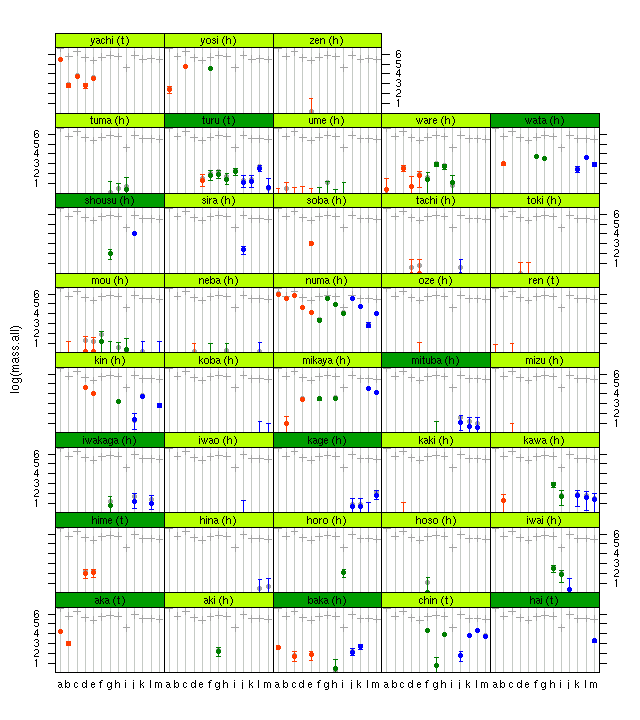
betaS[Sp, 1]
と
betaS[Sp, 2]
は単に葉面積と分枝速度の負の相関,
なんだろうけど
betaS[Sp, 2]
と
betaS[Sp, 3]
のあいだの負の相関は何だろう,
と図にしてみたら
……
なるほど,
こういうことだったのか.
re[i] ~ dnorm(0.0, tau)
みたいな定式化はさけろ,
ということです.
もちろん,
たとえば一個体から何回もサンプリングしてる場合とかは
しょうがいないけど.
\documentclass{seminar}
だとそういうのが面倒なんだよね.
print.bugs()
出力をよみこみ,
それに対応する要約を付加した PukiWiki 用テキストファイルを
生成させてみる.
一時間ほどの試行錯誤でうまくできた
……
しかし最後に file permission を変えたり,
といった作業は手動になる.
PHP の動作ユーザー apache,
ってのは変更不可能なのかなあ
……

pipetree
うごかす.
そっちはいいんだが,
作図担当の
POV-Ray
が ver.3.6 になって挙動が少し変わった
(挙動というか,
引数の与えかたや ~/.povray/).