ぎょーむ日誌 2006-12-22

2006 年 12 月 22 日 (金)

• 0750 起床． 朝飯． コーヒー． 0930 自宅発． 曇． 0935 研究室着．
• 査読報告かきのつづき．
• 志水さんと地衣類相談． ちょっと前の 計算 なんだけど， われながら記憶がぼろぼろに脱落している， というか． 思えば 10 月後半のこの計算いらい， ひたすら WinBUGS をあたかも「実戦化のための訓練」 であるかのよーにひたすら走らせ続けてきたなぁ ……
• 今日はいろいろな用件とかで院生密度が低く， 静寂だ．
• わりといいかげんな査読報告を書いてしまう． 1245 送信． 一件落着． 昼飯． 人口密度が低いのでのんびりと．
• R-help のやりとり見ていて思い出したんだが …… R の線形混合モデル・一般化線形混合モデルを計算してくれる library(lme4) の lmer() の結果はそれぞれ lmer・glmer クラスのオブジェクトになるのだけど， これらをベイズモデルとみなして MCMC 計算やってくれる mcmcsamp() という関数も library(lme4) に同梱されている．
• たとえば

  fit1 <- lmer(y ~ (1 | group), family = binomial, method = "Laplace", ...) # glmer オブジェクト
  mcmc1 <- mcmcsamp(fit1, n = 500) # library(coda) の mcmc オブジェクト
  

  で何やら MCMC 計算やってくれるんだけど …… 実験してみると random effects の事後分布の計算， 何やってるのかよくわからんなぁ．
• help(mcmcsamp) によると，

  The prior on the fixed effects parameters is taken to be locally uniform.

  fixed effects は何やら一様な (局所的) 無情報事前分布で， random effects は

  The prior on the variance-covariance matrices of the random effects is taken to be the locally non-informative prior described in Box and Tiao (1973). Conditional on the current values of the random effects these are sampled from a Wishart distribution.

  平均ゼロの多変量正規分布から得られている， と． その分散共分散行列の無情報事前分布 (つまり超事前分布 hyper prior) は逆 Wishart 分布． まあ， ふつーの階層ベイズモデルっぽいことやってるわけで．
• えーと， てきとうに例題を作って

  fit1 <- lmer(y ~ (1 | group), family = binomial, method = "Laplace", ...) # glmer オブジェクト
  

  をやると

  Generalized linear mixed model fit using Laplace 
  Formula: y ~ (1 | group) 
   Family: binomial(logit link)
    AIC  BIC logLik deviance
   1385 1395   -690     1381
  Random effects:
   Groups Name        Variance Std.Dev.
   group  (Intercept) 0.0353   0.188   
  number of obs: 1000, groups: group, 10
  
  Estimated scale (compare to  1 )  0.9976 
  
  Fixed effects:
              Estimate Std. Error z value Pr(>|z|)
  (Intercept)    0.108      0.087    1.24     0.22
  

  となり， さらに

  mcmc1 <- mcmcsamp(fit1, n = 500) # library(coda) の mcmc オブジェクト
  

  やってから (library(coda) も忘れず実行) summary(mcmc1) やると

  Iterations = 1:500
  Thinning interval = 1 
  Number of chains = 1 
  Sample size per chain = 500 
  
  1. Empirical mean and standard deviation for each variable,
     plus standard error of the mean:
  
                     Mean     SD Naive SE Time-series SE
  (Intercept)       0.109 0.0999  0.00447        0.00528
  log(grop.(In))   -3.391 1.1070  0.04951        0.14390
  deviance       1385.842 6.2637  0.28012        0.47325
  
  2. Quantiles for each variable:
  
                     2.5%       25%      50%      75%    97.5%
  (Intercept)      -0.084    0.0474    0.104    0.169    0.318
  log(grop.(In))   -6.022   -3.9808   -3.269   -2.629   -1.521
  deviance       1375.724 1381.4101 1385.200 1389.406 1399.566
  

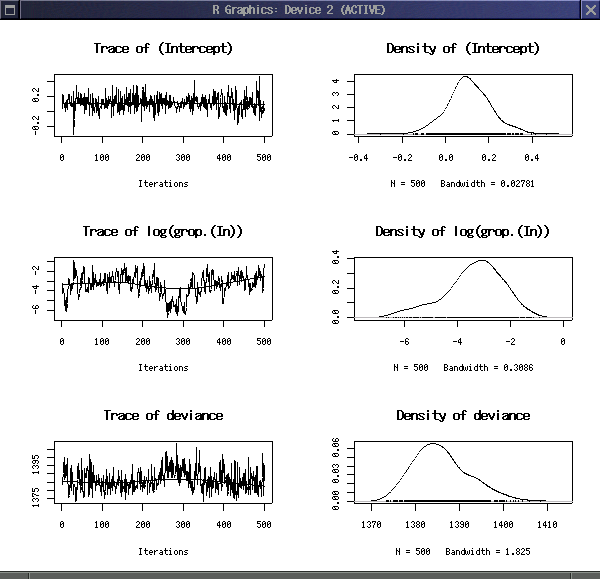
  で fit1 と summary(mcmc1) を比べてよーやくわかったんだけど， MCMC 計算の結果に含まれてる log(grop.(In)) ってのは group の random effects (つまり group 差) あらわす事後分布の分散の log になってるわけね． plot(mcmc1) すると， いつものごときこういう図になるわけで．

• つまり線形混合モデル・一般化線形混合モデルの階層ベイズモデルの MCMC 計算は R2WinBUGS なんぞ使わずとも lmer() & mcmcsamp() 使えばできるらしい， ということですな． ふーむ …… とやや驚いたので 「生態学のデータ解析 - lmer MCMC 計算」 なるペイジを追加．
• で， ついでについついこのデータ解析サイトのあちこちも変更してしまう．
• 私はなぜかくもうだうだしてるのだろうか?
  1. 今年最後の査読ぎょーむが終了したから
  2. 院生密度が低くてのんびりできるから (年内に完了すべき院生したうけぎょーむはまだ残存してるが)
  3. 12/27 (水) しめきりの 助教書類 書くのがイヤだから
• とも言ってられないので書類の準備． 途中でイヤになってお茶部屋に逃げようとしたら， 院生密度がいつのまにか平常の値にもどっていたので， こそこそと逃げだす．
• 完成度 40% ぐらい? で本日は撤退． 1920 研究室発． なんかホントに雪がぜんぜんつもってないな …… 1935 帰宅． 体重 70.6kg． 晩飯の準備． 晩飯．
• この ひと月 でさらに体重 1kg ほど減少したのはいいんだけど (下うけやせ?) …… どうも空腹状態で晩飯くうと カラダの血液のたいはんが胃のまわりにあつまるかんぢですなぁ． アタマが働かない．
• [今日の運動]
  • 腹筋運動 30 × 3 回． 腕立ふせ 5 × 3 回．
• [今日の食卓]
  • 朝 (0820): 米麦 0.5 合． 海藻スープ．
  • 昼 (1300): 研究室お茶部屋． 食パン．
  • 晩 (2110): 米麦 0.7 合． マイタケ・ワカメ・ホタテ・豆腐のシチュー．