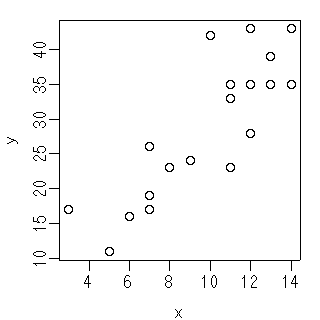
[こういう架空データ]
いちばん簡単に,
子供 (新生児) の個体数がその集団の親の個体数に
「比例」
している状況.
現在、A棟地下機械室にて蒸気漏れが発生しています。 湿度が非常に高くなっておりますので、機械室に置いてある物品等に 湿気による不都合がありましたら、搬出等の対処をお願いいたします。
library(MasterBayes)
して
vignette("MasterBayes.Tutorial")
と命じると全 61 ペイジにおよぶ親切なる解説 PDF ファイルがひらく.
offset()
わざミニ解説.
いま研究集団対象が 20 個あり,
そこにいる「親個体の個数」
x
が
> x [1] 13 11 12 7 7 12 14 10 7 9 8 3 14 13 6 5 7 12 11 11で, ある年にこれらの 20 個の集団で新しく生まれた子供の数
y
は
(x と順番おなじで)
> y [1] 35 23 28 26 19 43 35 42 17 24 23 17 43 39 16 11 17 35 33 35とする (どの親が何個体の子供を産んだ, というのはわからないものとする).

(集団内の新生児の数) = (親の数 x) * (一親の平均産仔数)とモデル化し,
(y の平均値) = x * exp(線形予測子)として (線形予測子とはいつもの
b0 + b1 * x1 + b2 * x2 + ...
のこと),
さらに集団ごとの親の個数
x
を
offset 項
として
(y の平均値) = exp(線形予測子 + log(x))とおけばよい (offset 項である
log(x) には係数がない).
y
は 0, 1, 2, 3, ... の値をとるので,
(一番簡単には) ポアソン分布
にしたがうと考えられる
((y の平均) = exp(...)
となっているので link 関数は log).
これを offset 項いれて
R
の
glm()
で計算させるには,
glm(y ~ 1, offset = log(x), family = poisson)としてもよいし,
glm(y ~ offset(log(x)), family = poisson)でもよい.
glm(y ~ area + food, offset = log(x), family = poisson)といった定式化になるのだろう. ともあれ, 特にカウントデータの解析には 割算いりません, ということで.