KuboLog 2006-09-21

2006 年 09 月 21 日 (木)

0650 起床． 0705 自宅発．晴． 0720 研究室着．朝飯．コーヒー．

うだうだとぎょーむ日誌を書いてみたり．

また大陸奥地から面倒を招来しそうなもめごとの原因になりそうなメイルがきたので，まずはそちらでよく話あってください返信．

小林さんからダケカンバ葉っぱの光合成速度と蒸散速度のデータおくってもらったので，それぞれの光 vs 速度曲線を作図してみる．

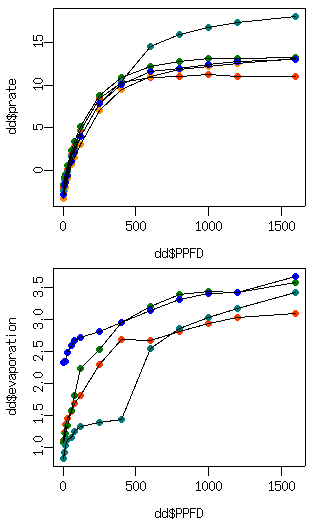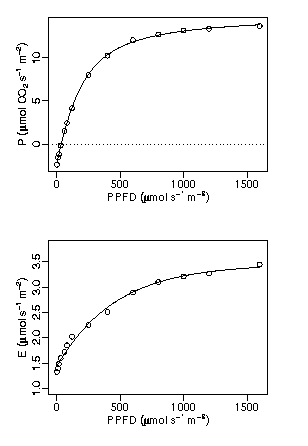
[とりあえずこういうかんぢ]

で論文用の曲線を推定・作図しなおした．林冠の合計生産力や蒸散量はあとから計算しなおす予定 (といっても自動作表プログラムを動かすだけだけど)．
光合成速度 (上) のほうは 5 枚の葉のデータに (いわゆる) 非直角双曲線 (呼吸量もいれて 4 パラメーター)，蒸散速度 (下) のほうは 4 枚の葉のデータに私がでっちあげたてきとーな式 c - (c - a) * exp(-b * I) という 3 パラメーターモデルをあてはめたもの．
ここでの fitting には R の nls() 使った．

これらの「セン」はいっけん問題なく見えるけれど，統計学的・生物学的にいろいろと問題ありありだ …… しかし，この林冠モデル論文の眼目は「精密な推定をすること」ではないので，上のいんちきくさいセンを使う予定なんだけど．

気になるひとつの点は「個葉差」である．この測定では一枚の葉から何度もデータをとる，つまり典型的な pseudo-replication になっているわけで，そのあたりは「個葉差」図示される．

[個葉差]

上が光合成速度，下が蒸散速度．
生理生態学では同じ個体とか葉っぱから何度もデータとることが多いのに，そのあたりまったく考慮しないでパラメーター推定とかやってんのはかなりヘンだよねえ，とかねがね思っていたわけですが ……

こういう状況では random effects を考慮した統計モデリングが役にたつはずだ …… ということで，論文用の計算とは別に nlme() in library(nlme) でためしに推定してみる．

fit.mixed <- nlme(
	prate ~ f.prate(f, q, pmax, respiration, PPFD),
	data = data.photosynthetic.rate,
	fixed = f + q + pmax + respiration ~ 1,
	random = q + pmax + respiration ~ 1 | id,
	start = c(f = 0.06, q = 0.7, pmax = 13, respiration = 2)
)

nlme() はなんでもかんでも正規分布かつその平均値は (とうぜんパラメーターに関する) 非線形な関数でよい，つまり非線形混合モデルを計算してくれるわけだ．なんでもかんでも正規分布のご利益で複雑な random effects を指定できる．このあたり GLMM とは異なるところだ …… とはいえ， random effects をになう項を複雑にするとかなり計算に時間かかるけど．

で， random = q + pmax + respiration ~ 1 | id, なる random effects 構成は AIC (ABIC?) 的に最良の random effects だったわけだが …… うーむ，この観測データ & このモデルの組み合わせのもとでは，混合モデル化することによってあてはまりは格段に改善されるものの，パラメーターの最尤推定値そのものはほとんど変化しないなあ ……

Nonlinear mixed-effects model fit by maximum likelihood
  Model: prate ~ f.prate(f, q, pmax, respiration, PPFD) 
  Data: dd 
  Log-likelihood: -22.214
  Fixed: f + q + pmax + respiration ~ 1 
          f           q        pmax respiration 
   0.064786    0.614758   17.456469    2.188832 
Random effects:
 Formula: list(q ~ 1, pmax ~ 1, respiration ~ 1)
 Level: id
 Structure: General positive-definite, Log-Cholesky parametrization
            StdDev  Corr         
q           0.20057 q      pmax  
pmax        3.77612 -0.997       
respiration 0.54150 -0.296  0.219
Residual    0.23171              
Number of Observations: 70
Number of Groups: 5

えーと，どういう計算しても最大光合成速度 (明るさ無限大? における光合成速度?) が 17μmol あたりになるってのが気になっているんだよねえ …… たいていの葉は 13μmol ぐらいでアタマうちになってんのに， 17μmol ってことはないでしょう，と思ったわけだが．

つまり個葉差考慮した統計モデルでも推定値があまり変わらない，ということは

非直角双曲線なる関数型で光-光合成関係を記述するのは不適切である (光強度「無限大」における光合成速度なんかをもちだしてくる数理モデルがおかしい)
こういうモデルで得られた推定値，たとえば「最大光合成速度」とかを生物学的に文字どーり解釈してはならない

まあ，上のふたつはどちらもだいたい同じコトをいってるんだけど，こういうハナシなんでしょう．いやはや，今回の林冠モデルの応用例として計算してみせる林冠生産量・蒸散量の憶測値試算みたいに，ある光強度範囲における現象論的な関数関係さえわかればよい，というときには問題にはならんわけだけど．

なんともはやー，とゆー気分になってきたので，お茶部屋かたづけで気分転換．ついでにお茶．時刻は 1110．

生理生態学データを混合モデルで解析しろ，というのは一個の独立した研究になるんじゃないかなあ，と思ったんだが．生理データ，というけど lme/nlme 本みればわかるように，混合モデルはとっくの昔から人間・動物の生理データ解析に頻繁に使われている．植物生理学まわりが遅れてるだけ，ってことかしらん?

ホントにここまでの計算とかまちがってないだろうなあ，と何度もチェックしなおしてみたり．

ついに「ひょっとして関数型そのものを間違ってるんぢゃなかろーな」というところまで気になる．文献ファイルには Thornley (1976) などともっともらしくあげているわけだが，これまたインチキなことに私はこの「植物生理学の数理モデル」なる教科書をもっていない．しょうがないので，またネット上などで検索してみると …… Thornley 御大の近著論文，ちょっと粘着じみたものを感じさせるタイトルの論文みつけてしまいましたよ．

Thornley, JHM. 2002. Instantaneous canopy photosynthesis: analytical expressions for sun and shade leaves based on exponential light decay down the canopy and an acclimated non-rectangular hyperbola for leaf photosynthesis. Annals of Botany 89: 451-458. (url)

とりあえず当方の数式でまちがいなし，か．上記論文，びみょーな諧謔とやや偏執ぎみな雰囲気に気圧されてしまったので，これって魔除けにでもなるかも，と文献ファイルにまつっておくことにする．

昼飯．

まあ，昼飯前のアレで光合成・蒸散速度の光依存性がわかってしまったことにしてしまって，モデル林冠のあれこれを再計算．作図・作表のやりなおし．まあ，このあたりはいつものごとく「なんべんでも最初から計算やりなおしできる」よう半自動化されているわけだが．

本文のなおしにとりくむ． LIDAR 文献あつめてみたり．小林さんがこちらに寄ってくださったので，書き直しについて相談．

1810 研究室発． 1825 帰宅．体重 73.0kg．晩飯．

[今日の運動]

うんどう休養日がつづいている

[今日の食卓]

朝 (0740): 研究室お茶部屋．食パン．
昼 (1355): 研究室お茶部屋．食パン．
晩 (1930): 米麦 0.7 合．卵焼き．ネギ・豆腐の味噌汁．

ぎょーむ日誌 2006-09-21

2006 年 09 月 21 日 (木)