ぎょーむ日誌 2005-05-17
2005 年 05 月 17 日 (火)
-
0910 起床.
どうも夜中に勉強すると生活周期が不規則になりがち,
という気がする.
朝飯.
コーヒー.
1015 自宅発.
曇.
1030 研究室着.
-
葉寿命勉強のつづき.
これって,
かなりおかると的な分野ではなかろーか.
ココロ正しきもののみが奇蹟をまのあたりにできる,
というような
……
などと書いたらまたお叱りをうけるんでしょうな.
-
植物生態学のたいていの
「多変量」
なデータ解析では多重性は考慮されることはない.
random effects という概念もない.
いわんや系統関係を考慮した種間比較はありえない.
強調されるべきは,
どういうふうに数値をこねくりまわしても
consistent な結果が常に得られる,
すなわち現象を生起させている神の御心を
「自分は知っている」,
この一点のみである.
信仰の強さが問われているともいえる.
この文脈において,
観測値の平均をとって情報を「浄化」して
対数変換するのは唯一絶対真実に近づく正しき道である.
なぜならば,
個体差だの非線形性だのは
悪魔が信仰の弱い人間をたぶらかそうとするたくらみにほかならないのだから.
-
……
などとですね,
このへんの文献よむときのココロの平和を実現すべく,
かかる歪んだ極論をでっちあげてみる.
えー,
いつも忘れてはならぬのは
……
数値をごちゃごちゃするばかりのわれわれモデル屋は
「自分は自然現象を研究している」
といったおめでたい錯覚におちいるべきではなく,
むしろそう信じて疑わない自然観測者たちの不思議なる心象を
冷静に観察しうる立ち位置に身をおくこと,
とゆーあたりだ.
そう,
冷静に.
-
で,
とある論文では
「あとづけ」で系統関係をうんぬんしてるやつがあるな
(査読者に指摘されて追加したのか?).
しかし読んでみると
「そんなの考慮しなくてもぜんぜん問題ないんだ」
という主張に終始しているだけだな.
ふーむ.
-
しかし,
まあ,
系統関係を種間比較って,
以前にちょっとだけ勉強したわけだが,
偽の相関を削りとるついでにとりだせる情報も激減する,
という側面はありますわな
……
それぞれの状況にあわせて何か工夫ができるのかもしれないけれど.
-
で,
別の論文ではせっかくいろいろな齢のシュートの葉をかたっぱしから
測定しているのに,
齢ごとに平均して情報をツブしていたり.
樹木のカタチを想像してもらえればわかるように,
シュートの本数は若い齢のものほど多い.
しかし,
平均なんぞに圧縮してしまうと,
数十本の当年生シュートのデータも一本しかえられなかった
10 年生シュートのデータも一つの統計量に圧縮されてしまう
……
とでも指摘したら
「それのどこがダメなのか」
と不思議がられるのかもしれんな.
-
常緑樹の落葉パターン,
こまかい時間間隔でおっかけると季節性の影響がもろにでて,
あたかも意味ありげな振幅みたいなものが見えてしまう,
ということなのかな.
いや,
季節性はべつに無意味なわけではないけれど.
-
生命保険の売りこみを避けるために,
1200-1300 の時間帯は北大構内走にでも出ているべきかもしれん.
しかしテキはこちらを捕捉するまで巡回運動をやめないわけで
……
-
1300 より
研究室セミナー
,
本日は M2 牛原さん.
植物の葉っぱ形質とくに葉寿命は何で決まるか,
という界隈の論文 (上述あれこれ) の紹介.
データ解析はいいかげんなまま放置しとくくせに,
窒素・炭素をパーツごとに分画していく方向には熱心らしい
……
で,
系統関係考慮した種間比較うんぬんについて聞いてみると,
この問題にかかわる皆さん
「分類群ごとに比べればいいんじゃないの」
「わからん」
「いらん」
ということのよーで
……
-
植物生態学研究者って,
種分化は繁殖器管 (花) で生じるもので,
栄養器官 (葉) なんかは種内でもどんどん勝手に変わっていって
(ecotype つくりまくりとかで),
もはや系統関係も反映しないほどに入り乱れた状態が維持されている
(遺伝子の発現・抑制なんかも環境に応じて自由にできる)
とでも考えているのかしらん.
-
セミナー後に昼飯.
先日から試行錯誤してる
(サーヴァー型とでもいうべきなのか)
tDiary
の使いかた講習
……
とゆーか個人チュートリアル.
まあ,
これは教えることもほとんどない,
ということがわかった.
さすがわ,
ゑぶアプリケイションソフトウェア
(もどき?).
-
7F 図書室撤収準備のスクリーニング作業.
20 冊ほど数理・統計学関係の本を救出する.
-
1915 研究室発.
1930 帰宅.
晩飯.
-
昼間から気になってる
「系統関係がニセの形質間相関をつくりだす」
例を考えてみる.
紙のうえにラクガキしてるうちに,
簡単な種分化モデルでそれが示せる,
とわかった.
-
R
プログラミングに没頭してしまう.
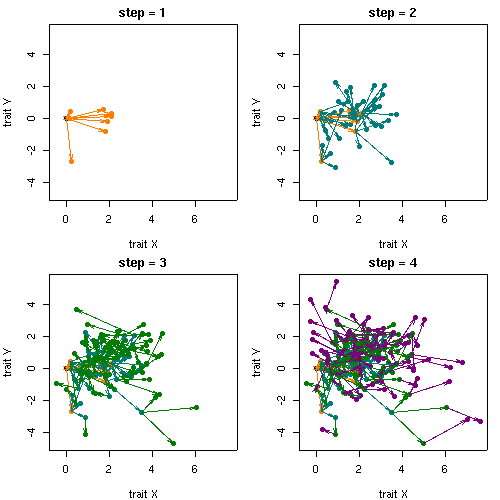
結果はたとえばこういうかんぢで.
形質 X と Y のあいだには一切の trade-off が無いにもかかわらず,
種分化がによって
「ニセの負の相関」
が生じてくる事例である.
-
時間 t で誕生した「母種」
は時間 t + 1 でいくつかの「娘種」
をつくりだす,
というモデルになっている.
こういう手順で生成する:
-
分化: 母種の形質 X と Y にそれぞれ
独立な正規乱数
(平均ゼロ --- つまり方向性ナシ)
をくわえて娘種の形質値を決める.
-
淘汰: 淘汰は母種と娘種の関係できまる.
それぞれの母-娘種くみあわせにおいて,
形質 X もしくは Y のどちらかが淘汰される形質 Z
(∈ {X, Y})
としてランダムに選ばれる.
母種より形質 Z の値が小さい娘は淘汰される
(たとえば上の step = 1 において,
形質 Y が母種より小さい娘種は淘汰されている;
形質 X はどんな値でもよい).
-
新しく誕生した娘種を次の時間ステップの
母種とする.
1. にもどる.
とゆーふうに,
-
形質 X と Y のあいだに trade-off なし;
とってよい値の範囲に制約なし
-
淘汰は形質 X と Y のどちらかにだけかかる
(母種より大きいものだけが残る)
という仮定で上のようなパターンが簡単に生成される.
これらの制約はもっとゆるめても
「ニセの負の相関」
が生成されるだろう.
-
もちろん乱数まかせの進化なんで,
「ニセな相関」
がでない場合もある.
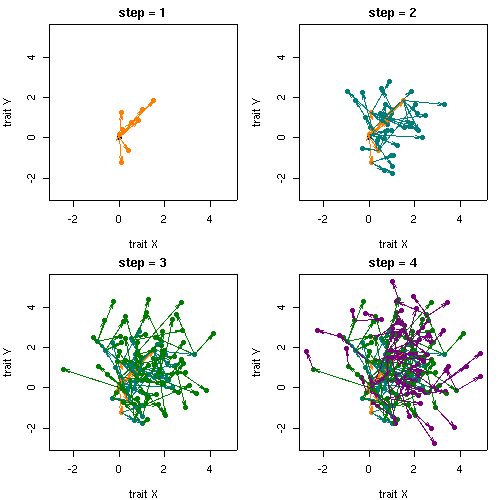
たとえば,
これは上よりは少しぼやけているかも.
-
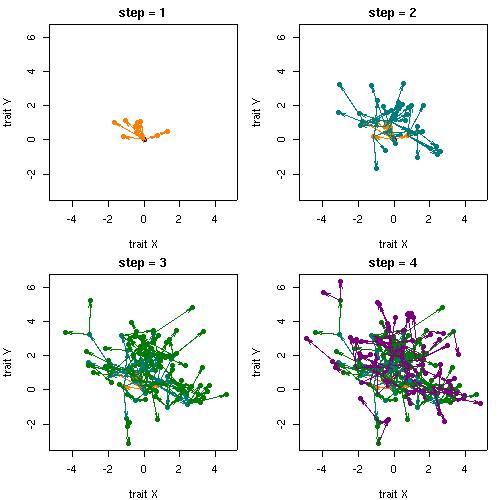
そして種分化がススんでも無相関みたいだ,
という例もつくり出されたりする.
-
まあ,
(パターンはっきりしない場合もあるけど)
trade-off ぬきで「ニセの負の相関」が簡単に作れるらしい,
とゆーことで.
-
なぜそうなるのか?
答えは簡単で,
これは二次元空間上の
「進行方向をあるていど制約された」
ランダムウォーク (というかランダムジャンプ)
になっているからだ.
形質 X と Y が増大する方向 (斜め右上)
にススんでいく「前線」が形成される
(場合が多いみたいな)
ので,
あたかも X-Y 間に trade-off あるように見えるのである.
-
某卒業生氏,
会社ヅトメをやめて
環境省「傭兵」
やるそーで
……
まあ,
がんばってくだされ.
-
あらら,
時刻はすでに 2600.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0930):
ヨーグルト.
- 昼 (1520):
研究室お茶部屋.
米麦 0.7 合.
タマネギ・ネギ・エノキダケ・コンブ・サケの味噌汁.
- 晩 (2030):
米麦 0.7 合.
タマネギ・ネギ・エノキダケ・コンブ・サケの味噌汁.