ぎょーむ日誌 2005-05-13

2005 年 05 月 13 日 (金)

• 0750 起床． 朝飯． コーヒー． 0920 自宅発． 晴． 今朝は気温たかい． 10°C こえてる． 0935 研究室着．
• 起床してから 1-2 時間は， うだうだと確率論的モデルについて アタマのなかでヒネってることが多いんだが (研究室でも自宅でも道路上でも) …… さいきんはマルコフ確率場 (Markov Random Field; MRF) の定式化の方法について， よくわからぬまま右往左往してる． 先月末から今月にかけて， 観測データとこのテのモデルをどう対応づけるか， という部分については理解がススんだ． というのも， 乱数パターンをどう生成し (forward 過程) そこからパラメーターをどう最尤推定するか (inverse 過程)， これら両過程を矛盾なく書けるようになってきたからだ．
• しかしながら， こういう具体的な部分はわかってきたのだけど， MRF の標準的な定式化とつじつまをあわせるやりかたがよくわからない． たぶん， ぜんぜん難しくない問題のはずなんだが．
• このあたり理解するカギのひとつは Hammerseley-Clifford theorem で …… といっても， これはあたりまえのことで， 「局所的」 相互作用の集積として定義される MRF が (大局的な) Gibbs Random Field と同値である， という …… そもそもこれがなければ Markov Chain Monte Calro (MCMC) 法 なんぞ使えやしない．
• …… というふうに書いてみると， わかってないポイントはずばり 「MRF 上のいわゆる auto-logistic model と (このたぐいのモデルの理解のもとになる) Ising model ってびみょーに違うんでは?」 というだけのこと， のようで．
• このあたりナヤみつつ検索してみると …… Stan Z. Li (李子青) の Markov Random Field Modeling in Computer Vision なる画像処理の本 (現在は第二版 Markov Random Field Modeling in Image Analysis が出ている) の第一章が公開されてんのをみつけ， その 1.3.1 小節 ``Auto-models'' において 最近傍だけみる auto-logistic model は Ising model と同じ， とある． ホントにこれって等価なのかな?
• よくわからんので， ちょっと発想の視点をかえてみる． たとえば …… 物理屋どもは Ising model を Metropolis 法で計算するとき， どういった手順でやるんだろうと想像してみることにする． 配置パターンの出現確率は大局的に記述されてるわけだが， ある場所を反転するかどうかはその最近傍だけで (局所的に) 決まる． そして Metropolis 法の 1 step で とりうる状態は「反転する」「しない」のふたつだけで …… と考えつつ Gibbs sampler (条件つき状態遷移確率) を書いてみると， 「その他」の部分は分母・分子で cancel out， 残った部分 (注目している場所のまわり) は auto-logistic そのものである， とわかった …… いまさらながら． えーい， ホントにいまさらながら， だ．

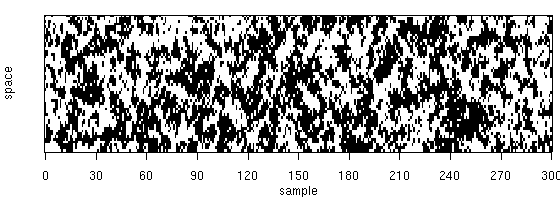
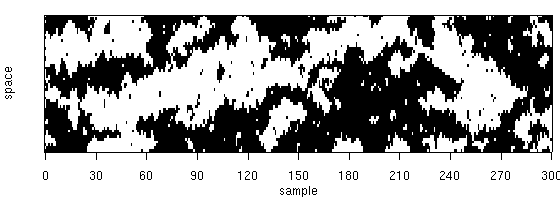
• とゆーことで， 上述の「最近傍の auto-logistic model は Ising model と等価」 という基本事項がようやくにして理解できた． たしかに 「ぜんぜん難しくない」 問題だった． いやはや． こんなのにこれまで合計何十時間を費してしまったのやら ……
• …… などと呆然としてると時刻はすでに 1200．
• まあ， これがわかったということで， あの (少なくとも数式の書きかたに関しては) かなりアヤしい Hubbell たち (2001, Ecological Research 16: 859-875) のバロコロラド樹木死亡解析の変てこなる数式どもが 本来意図していたはずの内容については， 完ペキに理解できた． 自分で説明をゼロから (Hubbell たちよりはいくらかでもマシになるよう) ぜんぶ書き直せる． まーこれも， いまさらながら， なんだが．
• 彼らの説明がなぜ難解だったのか? (あのどくとくな表記法はおくとして) こういう順番でいろいろな概念が説明されてんだけど，
  1. pseudo likelihood estimator の定義 (による空間構造ありモデルの説明)
  2. (1. では問題解決できないんで) Gibbs 分布の導入
  3. 2. から導出される Gibbs sampler の定式化 (形式的には 1. と同じ)
  これら相互のつながりがすごく悪い (あるいは書いたヒトたちもよくわかっていない) んだよね． 1. と 3. の区別ついてんのか? といったあたりとか． かくいう 私自身も つい数時間前まではここらへんが判然としてなかったわけだが ……
• ひとくぎりついたんで 1310 北大構内走． 晴． 1355 研究室もどる． 北大生協に昼飯調達しにいく． 書籍部にトラップされてしまう． いやはや， ひさしぶりなんで． 研究室もどって昼飯．
• さて， アカマツ原稿を …… と思ったら甲山さんが阿寒 「どりる」 雑談にきたので， それが引き金になって またややこしー統計モデリングの世界にひきもどされてしまった．
• 発端になった人物は自分がしゃべるだけしゃべって去っていったわけだが …… 甲山さんがこれの解析に使えると考えてる 「移動平均法」ってのはこういう 「時系列的なデータ」 に関しては有用ではない， というか自然科学で使うべき方法ではない． いやはや， 年輪気候学とかでしつこく使われてるけどね．
• この アヤしげドリル (あるいはこれの 輸入代理店) のノイズまみれなデジタル出力から 「年輪」 よみとるのは (そもそもこれって「年輪」よみとる機械ではないんだが) そうとうに面倒な統計モデリングが必要である． 理想的にはいろいろな誤差を表現する確率分布をたたみこみつつ
  1. ある個体の「年輪」を読み取るのに 他の全個体の情報を利用する
  2. 改善されたある個体の推定結果を全体に反映する
  3. べつの個体を選んで 1. にもどる
  をひたすらくりかえしてより良い (尤度の高い) 推定を得る (つまり「年輪」よみと同時に成長モデルのパラメーターも推定する) …… というのがおそらく最良の解法のひとつだ． カーネル推定とかになるのか? あるいは各観測点を 視細胞 のようにみたてて， それらの間で側方抑制みたいな neural network を構築して …… いづれにせよ， またしてもまたしても MCMC 法 & Bayesian inference にほかならない．
• なんでもかんでも MCMC だの， 面倒になったらすぐにべいぢあん， という考えかたはちょっと阿呆っぽくてイヤかも …… と思いつつもそのあたりの文献よみに没頭してしまったり．
• しかし， いくら読んでもできあいの答えが書いてあるわけでもなし， またきちんと考えるとどんどんそちらに時間とられるので， こういう難問とはうかつに関わらないほうがよいですな． のんびりと 「ドリル」問題なんぞやってる場合でもないし． 放置だ． まずはアカマツ， 寄生ハチ問題その他をかたづけて， ですね ……
• しかし他のことは進捗せづ， 撤退． 2020 研究室発． 2035 帰宅． 体重 74.4kg． 晩飯．
• 上のような図をつくる R プログラミングにのめりこんでしまった ……
• [今日の運動]
  • 北大構内走 45 分間．
• [今日の食卓]
  • 朝 (0830): チンゲンサイ・卵の炒めもの． ヨーグルト．
  • 昼 (1510): 研究室お茶部屋． 北大生協サンドイッチ．
  • 晩 (2130): スパゲッティー． ニンニク・豆板醤のソース． キュウリ． タマネギ・サバのマイクロウェイヴ酒蒸し．