ぎょーむ日誌 2003-07-16

2003 年 07 月 16 日 (水)

• 0710 起床． 朝飯． コーヒー． 0820 自宅発． 曇． 0830 研究室着．
• ぎょーむ日誌書きつつ Perl データマンジング本 などつらつらと見返す．
• さっさと仕事すべきなのに， 科研費で買った 実用 Perl プログラミング をぱらぱらと見てしまう …… かなり良い． この本を読んで， SWIG (simplified wrapper and interface generator …… swig には「がぶ飲み」という意味もある) というちょー便利そうなモノがあることを知った (いまさらながら)． 他にもデータ永続化とか有用な情報いろいろ． 1997 年原著出版ということで， やや古めかと思ってたけどそんなことはない． Perl をぎょーむで使わねばならぬヒトにとって， この実用 Perl プログラミング (Advanced Perl Programming) と Effective Perl は必携だろう． どちらも応用ワザのための基本を重視してるんで．
• さーて， いつまでもふらふらとしてるわけには …… お， /.J にも R の紹介 が! ほらほら， ゑくせる統計関数 の壊れ具合がどんどん報告されてますよ (cf. 青木さん (群馬大) の 「ひどい話です!」)．
• ということで， ゑくせるやめますか， それともデータ解析やめますか．
• それはともかく， まだ解決しない粕谷さん宿題にとりくむ． ある小集団の平均値が確率変数として与えられ， かつその小集団内の標本もまた確率変数 (平均ゼロ) である， という混合モデル的状況 (後者の確率分布の平均がゼロなので random effect 的状況 というべきなのかもしれないが)． で， とりあえず確率分布がどちらも正規分布としている． 分散はありとあらゆるところで異なる．
• こういう計算やったらいいんじゃないでしょうか， ということでたたみこみ尤度方程式を書いたメモを先週つくったんだけど …… これではうまく最尤推定できない， ということがわかった (集団内分散と集団間分散がうまく分離されん)． Searle, Casella & McCulloch (1992) Variance Components なる書物に上と似たような問題における 尤度方程式が掲載されてると 粕谷さんが調べてくれたんだけど， 私のそれとは少しばかり異なっているんだよねえ．
• で， このあたりの相違が何によるものなのかよくわからん， という状況が続いている． よくわからぬまま午前終了． 北大構内曇天走． 昼飯．
• 午後も出典 Variance Components 数式をひねってみるけどよくわからん． そこでいったん自分の定式化をゼロから再検討してみる …… と， わかってしまいましたよ． 粕谷問題の想定をうまく定式化できていなかった． この nested 状況はよく考える必要があり， 小集団の平均は確率変数だけど， その小集団にとっては定数のごときものであり， そこを中心にして小集団ごとに異なる標本セットが得られる， というわけだ．
• というふうに数式を書き直してみると …… どひゃー， 多量の正規分布密度関数が積のカタチになって登場か! 正規分布ぎらいな私にとっては， わけわからんムシどもがひしめきあってうごめいている 小部屋にほうりこまれたような気色わるさを覚える …… かとーオフィスから逃げだし北大構内逃避の旅に出る． ただし紙束はかかえて．
• 北大生協の自販機紙コップコーヒ飲みつつ， 「えーと， 正規分布の積 → 和の正規分布 に帰着できるハズだ……」 とココロ落ち着けさせつつ計算問題に取り組む． そういう式変形を行い， かつ再生性を悪用するカタチにもっていこうとすると， おのずと小集団の標本平均と標本分散が導出されてくる．
• えらく難しい問題やってるなと思われるかもしれないけれど， 実際の難度は数式頻出分野でいうと 学部学生レヴェルの演習問題程度なんだが (じつは微分積分ができる高校生でも問題ナシ …… ただし初等的な統計学の理解が必要)．
• どうやら， (途中をはしょると) 下のようにまとめられるんでは， ということがわかってきた． f(., μ, σ2) が Gauss な確率分布密度で， Mi,j と Vi,j はそれぞれ小集団ごとの標本平均・標本分散．

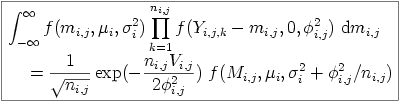
• これは Variance Components 本のそれに近づいている． Mi,j と Vi,j は十分統計量 (sufficient statistic) というやつだろうか， と思ったんだけどそうではなさそうだ． これらが導かれてきたのは f(., μ, σ2) が正規分布であることに強く依存している． 十分統計量なら確率分布にはよらないはず， と理解してるんだけど …… うーん， 実は f が指数関数族なら何でもいい， ということなら十分統計量と言えるのかもしれんなぁ． どうなんだろう．
• それはおいとくことにして， かとーオフィスにもどる． とりあえず粕谷さんに連絡メイル． それから， ここまでの計算を LaTeX でまとめてみる．
• どうやら粕谷さんのほうも小集団ごとの 標本平均・標本分散を使った定式化に気づかれたようで …… 私のやりかたとは少し異なるようだけど．
• カエデ下請けぎょーむで CVS リポジトリの挙動不審な点を 浦口さんと解明してみる …… ディレクトリ追加した場合は cvs checkout せんといかんの? 追跡調査が必要．
• 最尤推定問題は簡単化された尤度方程式が出る書きかけ状態で make dvi && make pdf してアップロードしておく． また連絡メイル． 今日はここまで．
• と思ったらお茶部屋に白板にはってあったパズルなどにはまってしまう． さらに M2 森君とマイクロサテライトによる父親探しの 確率論的モデルの検討． 2230 研究室発． 現金がないので買いもの行けない． 2240 帰宅． 体重 71.6kg． 晩飯． 計算あれこればて．
• [今日の運動]
  • 北大構内走 1235-1310． ストレッチング．
• [今日の食卓]
  • 朝 (0730): 米麦 0.7 合． キャベツ・タマネギ・ショウガ・鶏レバの炒めもの． トマト．
  • 昼 (1320): 弁当． 研究室お茶部屋． 米麦 0.7 合． キャベツ・タマネギ・ショウガ・鶏レバの炒めもの．
  • 晩 (2300): 米麦 0.7 合． レトルトパウチドのカレー． トマト．