ぎょーむ日誌 2001-02-14

2001 年 02 月 14 日 (水)

• 0750 起床． 眠いなぁ．
• 朝飯・弁当の準備． 朝飯． う． 時間か．
• 0815 自宅発． 曇． 曇天な毎日． 0832 東京モノレイル流通センター発． 浜松町の気温 1 ℃． 0853 研究所着．
• さて， と． 「ニセ」アカマツ問題をぢりぢり進めなくてはならんのだが …… 今まで，茎という部品の 「ある時刻 (齢) での太さ」と 「茎ごとに固有な生長関数」が 一対一でばちんと対応していて (という仮定というかでっちあげというか)， その長さについては 観測された値をそのまま使う (不変)， という方針だったのだが …… そういえば「重さ」という観測値もあったなぁ， と思い出す． えーと， これはどういうふうになっていたっけ．
• all_dump.pl という手持ちデータを 全部出すスクリプトで調べてみると …… そうか， 「◯齢の茎の重さ」 というふうに齢ごとにまとめて 総重量を測定されてる． ということで， 「ニセ」アカマツ構成部品としては やはり (太さ，長さ) ペアが一番細かいわけだ． とはいえ， 材密度でも計算してみるか．
• なーんか， 実験区のほうが 「つまって」いてばらつき大きい， としかわからんな． さて， どうしよう．

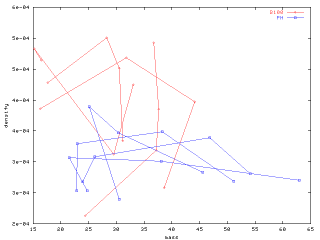[重さと材密度]
いや，相関を見てる
のではなく，処理区
によるばらつきの違
いを眺めてるだけな
んですけれど ……
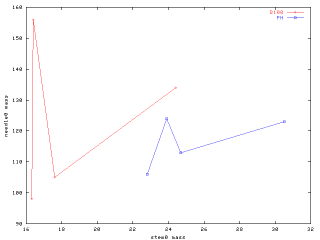[茎と葉の重さ (当年生)]
で，曝露実験とゆー
のをやると，葉っぱ
の量が増えるのに茎
は軽いんだよね．ト
レイドオフか効率低
下なのか ……

葉っぱの重さも 4 標本 × 2 処理区 だからなぁ …… 当年生シュートの個数の分布は 処理間でそれほど差がないように見える (とはいえ分散大きいし， やはり 4 標本どうしの比較なんだけど)．
• 昼飯を食いつつ取りまとめを考える．
• 生産は当年生茎だけが行うもの， としよう． 常緑とはいえ， 針葉の古いやつなんて生産には ほとんど寄与してない， ということらしいんで．
• えーと， 当年生針葉も存在しないことにしよう． むろん当年生茎そのものが光合成してるわけないんだが， それを言い出すと面倒になるばかりなので (観測データとの整合性などなどの問題あるんで)， 茎が光合成してるかのように見せかけるのである． ええ， そうですとも． そうに決まりました．
• さて， その茎の生産したものがどこに配分されるか， というと ……
  • (自分も含めた) 既存の茎の肥大生長． 各茎の肥大生長量は その茎に「固有な」 生長曲線によって決まってしまう． いやおうなく．
  • 新しく作る茎．
  むろん葉っぱ (針葉) も作られるんだが， それを言い出すと面倒になるばかりなので， 葉っぱの生産はここでは考えないのである． 証拠隠滅のためなら， 私が「ニセ」アカマツの葉っぱを むしって食べてしまってもよい．
• これらの配分先に回した重量の合計のことを純生産と 仮称することにして， (純生産)/(当年生茎の合計重量) を生産率と呼ぶことにする． この生産率なるパラメーターの値は 観測データを利用して計算できる． なんとならば， 「すべての茎は固有の生長曲線を内蔵しており， それは時間の関数である」 というでっちあげから， 観測樹木個体の「一年前」の状態が 決定されるからである． つまり現在の一年生茎が当年生であったときには コレコレのサイズであり (他の齢の茎も同様)， それがこの一年間でこれだけ太ったあげく， ついでに新しい茎をこんだけ作りました， と逆算してみせればよいだけだ．
• かかる作為的なサブモデルによって， 実験区の当年生茎集団による生産は 対照区に比べてますます貧弱になるハズ． 個体ごとに異なるとする生産率の値を 上のように「推定」してしまうと， そうならざるを得ないだろう， というのが読みスジなのである． 詳しくは， この生産率とかいうのを計算してみてから．
• さらに個体全体の体積膨張の速度は次第に鈍化する． 竹中さん言うところの 「シンク要求」 じゃないけど， 既存の茎も「固有の速度」とやらでもって ぶくぶくと太らねばならず (という仮定をすでに与えてしまったんで)， そちらに資源を取られて (古い茎が 「俺はこれだけ太らねばならんのだ」 と言って来るとその要求量は必ずぶんどられる)， 当年生茎の生産は少なくなるはずである． すると翌年の純生産はさらに落ちる， という悪循環である． やれやれ， 個体としてはすぐに破綻してしまいそう ……
• さーて， これで 「茎という個別の部品が単位なんだけど， (データ無いんで) それら部品間のつながりの見えない樹木個体モデル」 のアイデアは出そろったかな． では， ヤバいところにできるだけ触れないようにして， (部品間の相関を可能なかぎり 考慮しない) 帰無仮説的な動態モデルを考えるとしたら， その一試案はこうだ ……
  1. 当年生茎の総重量に 生産率なるもの掛け合わせて 純生産が決まる．
  2. 各茎の齢をひとつ増やす．
  3. 一年生以上の茎が要求する 肥大生長に必要な資源を純生産から 融通する．
  4. 余った資源を新しい当年生茎の 生産に充当する．
  5. 当年生茎に回す資源を 個別の当年生茎として分割する． 分割するサイズは 各当年生茎の「生長速度」 で決まる． その速度分布は 観察されている当年生茎の 速度分布を流用する．
• よくわからんけど， 材密度は個体ごとに固有ということで． そーすると， 実験区のほうが多少密になるワケですか． で， 長さは「速さ」とセット． 一緒に分布からひろってくる． これで 「速さ」→ (太さ・長さ) → 体積 → (材密度) → 茎重量 とつながりますかね．
• ま， あと三次元樹木図を作れと言われるだろうから， 例のいんちきな親-子分配法で当年生茎を 一年生の先端にでもくっつけてやればよろしかろう． 観察されてる速度分布からリサンプリングするので， 上記分配法は破綻しないのである． なぜ， 親子関係づけが処理の末端に位置してるかというと， こんな怪しげなサブモデルに樹木個体の挙動を 左右されるのはイヤだから， である．
• 観察されたというか強引に算出された速度分布から リサンプルするとなると …… 実験区では「遅い」個体が増えるだろうな． そうか． このあたりを 生産率に反映するようなモデルにすれば ……
• それはともかく， その生産率なるものを推定する Perl スクリプトでも 書いてみますか．
• …… なんてのは 面倒だなぁ， とネット上に逃避してると …… お， オアフ島沖の <LosAngels> 級原潜と 日本の水産高校実習船の衝突事故報道に隠れるよーに …… バレンツ海に沈んだ <Krusk> はやっぱ魚雷自爆でした って …… うーむ， ロシア人め． なんていんちきな． さんざん衝突説・陰謀説を連呼してたくせに．
• 生産率推定用兼シミュレイション用の 茎クラスをぢりぢりと書き始める． 今回は All Perl な方針なので， この「Perl モジュールでクラスを書く」 という作業に 面倒感がつきまとうのである． Perl でオブジェクト指向じみたことをやると あまり楽しくない． すでにいくつか「ニセ」アカマツ用の モジュール書いてんだが．
• とりあえず茎クラスが生産率推定に使えそうなところまで 書けてテストできたので帰宅準備． 腹減った． 1805 研究所発． モノレイル駅で定期券買う． 一月分 10300 円． 久しぶりに浜松町の本屋 dan に寄る． 付け焼き刃的ながらデータベイスに関する かなり初歩的な解説書を買う． 1830 東京モノレイル浜松町発． 1900 帰宅．
• またまた晩飯食ったら 2 時間ほど寝てしまった． そして「ニセ」アカマツの 生産率推定スクリプト書きがなかなか進まない．
• Tu-22 が北海道付近にて領空侵犯という報道． うーむ， ロシア人め． どうせ来るなら私が札幌にいるあいだに 北大上空を航過しろ． 見たかった， ツポレフの超音速爆撃機．
• 今日の朗読
  ``Analytical Population Dynamics'' (Royama, 1992)
  Part I Theoretical bases of population dynamics
  Chapter 2. Structures and patterns of population processes
  • 2.2 Pure density-dependent process
    • 2.2.5 Nonlinear second-order process
    • 2.2.6 Higher-order process
• ふつーな第 2.2 節もようやく終わりである． まず 2.2.5 ではやはり X(t) = f( X(t-1), X(t-2) ) なんだけど f() が非線形な関数である場合について， 計算例が紹介される． というのも， 非線形な場合はあまり記号操作的な解析は 有効ではないからである． 線形な場合との対応をよく考えられたパラメーターセットで もってあれこれと計算． 非線形なのでカオスみたいなのが出る場合もあるけれど， 著者は こういうのは面白いけど 実際の個体群ではカオスなんて稀じゃなかろーか， という冷静な見解を述べる． このあたりはハヤりものに弱いモデル屋たちとは 一線を画している． つづいて長い 2.2 の最後に位置する 2.2.6 では 三次以上の動態が紹介されそうになるけれど， 二次以下の動態をこよなく愛する著者によって， ごくあっさりと切られておしまい．
• 今日の食卓
  • 朝 (0800): 米 0.5 合． 一昨日の豆腐トマトソース残り．
  • 昼 (1215): 弁当． 米 0.9 合． 一昨日の豆腐トマトソース残り．
  • 晩 (1930): 米 0.6 合． 豆腐・葉タマネギ・シイタケ・麸の味噌汁． 煮干だし． だしがらも食う． ホウレンソウおひたしサバぶし麺つゆ味． お， 久しぶりに一汁一菜が実現．