
[札幌,風雪]
A 棟 8F から見た光景.
まさに真冬なみ.
午後からは晴れましたけど.

glm()
の factor
な説明変数の挙動.
そのとりあえずのまとめ.
どうもこの <pre>
な引用はちょっと読みにくいので,
そのうち「生態学のデータ解析」
にでも移動したいねえ.
GLM の factor な説明変数について少し調べてみました.
とりあえず glm() の family = gaussian の場合だけ調べてみましたが,やは
り水準の順番のつけかたを変えても,説明変数を WinBUGS モデリングでよくや
るように {0, 1} にしても特に結果が (推定値のばらつきも含めて) 変わるわ
けではない,とわかりました.
以下は,そのあたりを例示してみたものです.
----
説明変数が factor であるときの R の glm() の推定値とそのばらつきについ
て調べるために,とりあえず (一番簡単な) glm(..., family = gaussian)に対
応した例題データを生成してみます.データの性質としては下記のものです.
・glm(y ~ x) に対応したモデル (y のばらつきは正規分布)
・y の SD は 0.5
・x のクラスは factor で 3 水準 (A, B, C)
・水準ごとの真の値は A = 1, B = 2, C = 3
・水準ごとのサンプル数は A = 100, B = 100, C = 50
このような条件をみたすように rnorm() で生成した架空データ例を図示すると
このようになります.
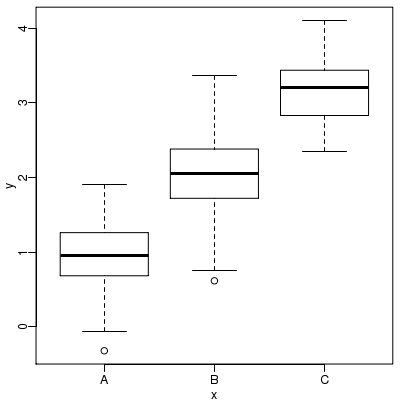
以下では,このデータを使って
1. 切片なしモデル (どうもこれが基本のように思えたので)
2. ふつうに glm(y ~ x)
3. x の水準をいれかえて,glm(y ~ x)
の三つの結果をを比べてみます.比較して確認できたことは「1, 2, 3 どれも
同じ結果になっている,ただし一見するとそう見えない」ということで,よう
するに factor の水準によって何か結果が変わるとかそういう話ではない,と
いうことです.
まず最初に切片なしモデルで水準ごとの推定値を得ました.
データは d という名前の data.frame に入っているとします.
[結果 1]
glm(formula = y ~ x - 1, data = d)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
xA 0.9543 0.0495 19.3 <2e-16
xB 2.0388 0.0495 41.2 <2e-16
xC 3.1617 0.0700 45.2 <2e-16
結果 1 の Std. Error (推定値のばらつき) について着目すると,推定値の
Std. Error がサンプル数に依存していることがわかります (A, B はサンプル
数 100, C は 50). C の Std. Error は A, B の sqrt(2) 倍になっています
ね.
次はふつうに glm(y ~ x, ...) やってみました.データ生成時にとくに指定し
なかったので,R はアルファベット順にA, B, C と水準に順番をつけ,A を
「基準」として B, C のずれを推定します.
[結果 2]
glm(formula = y ~ x, data = d)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.9543 0.0495 19.3 <2e-16
xB 1.0845 0.0700 15.5 <2e-16
xC 2.2074 0.0857 25.8 <2e-16
さて,まず結果 2 の Estimate (推定値) に関しては
・(Intercept) は結果 1 の xA と同じ (A が基準だから)
・結果 2 の xB と xC はそれぞれ結果 1 の xB - xA, xC - xA になっている
と簡単です.
それでは Std. Error はどうなっているでしょうか.
・(Intercept) は結果 1 の xA の Std. Error と同じ
というのは良いでしょう.それでは,いま仮に (Std. Error)^2 を分散と呼ぶ
ことにすると,
・xB, xC の分散は,それぞれ結果 1 における xA と xB, xC 分散の和
になっている
と言えます.xB を例にこれを説明してみましょう.結果 2 における xB は
0.0700 ですが,この値は結果 1 における xA と xB の分散の和の平方根つま
り sqrt(0.0495^2 + 0.0495^2) と一致します (理論的には本当に一致するはず
なのですが,数値計算における誤差で完全に一致しないこともあるようです).
結果 2 における xC,つまり結果 1 でいうと xA と xC の差についても同様で
す.
以上の計算は確率変数の平均・分散に関する計算から導出されます.
いま x1 と x2 が確率変数だとすると,
Mean(x1 + x2) = Mean(x1) + Mean(x2)
Var(x1 + x2) = Var(x1) + Var(x2)
という確率変数の和に関する公式はよく掲載されていますが,差に関しても同
様で,
Mean(x1 - x2) = Mean(x1) - Mean(x2)
Var(x1 - x2) = Var(x1) + Var(x2)
となります.Var に関しては和だろうが差だろうが足し算になるわけですね.
ついでに,factor の水準の順番を変えても結果が変わらないことも確認してお
きましょう.
d の x の水準の順番をいれかえた d2 なる data.frame を作り,
d2 <- d
d2$x <- factor(d2$x, levels = c("C", "A", "B"))
これを glm() で推定すると,以下のようになります.
[結果 3]
glm(formula = y ~ x, data = d2)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.1617 0.0700 45.2 <2e-16
xA -2.2074 0.0857 -25.8 <2e-16
xB -1.1229 0.0857 -13.1 <2e-16
ここに見られる Estimate や Std. Error も結果 2 の場合と同様に算出できま
す.
いずれにせよ,結果 1-3 は同じことを言ってるのであり,相互変換可能です
(数値計算の誤差があるので厳密には一致しませんが).たとえば結果 3 から結
果 1 を算出するには,
・Estimate に関しては引き算すればよい
・Std. Error に関しては,たとえば結果 1 の xA を計算するため
には sqrt(0.0857^2 - 0.0700^2) とすれば結果 1 の xA の Std.
Error に近い値である 0.04944 が得られる
となります.
glm() の他の family で同じようになっているかどうかはまだ確認していませ
んが,少なくとも近似的には同じような関係が成立しているだろうと思います.
----
……といったかんじで,かなり単純なものでした.ベイズモデルの場合は事前
分布の設定に依存しますが,無情報事前分布の場合は上記のような関係が成立
しているでしょう.