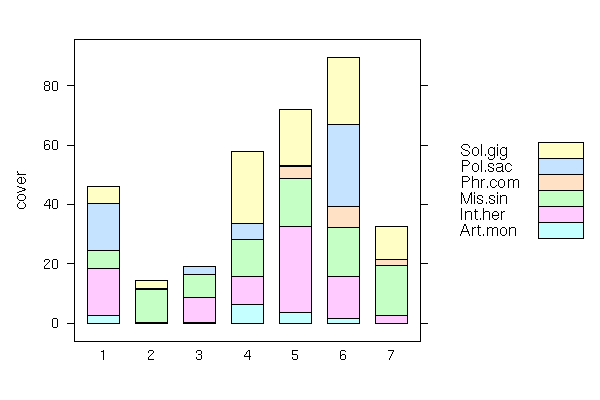ぎょーむ日誌 2008-04-25
2008 年 04 月 25 日 (金)
-
0740 起床.
朝飯.
コーヒー.
0930 自宅発.
晴.
0945 研究室着.
-
いぜんとして継続している放棄スキー場植生モデリングの
MCMC 計算,
昨晩かえりがけに投げておいた
全 5 樹種 20000 MCMC step は 4935 秒で終了してた
……
意外と速い.
分散共分散行列の次元が
3 × 3
から
5 × 5
になったにもかかわらず.
-
しかし収束は悪い.
ということで,
昨晩おもいついた改良を追加してまた試行錯誤な計算を
……
-
えーい,
計算にかまけてないでさっさと脱アリのためのアリ論文かきを終わらせたいのだが
……
-
しかしとうとうスキー場植生モデルは抜本的に改善された
……
全 5 樹種 (放棄スキー場数 5)
なのにわずか
6000 MCMC step (計算時間 1333 秒)
で「ぴた」と収束したねえ
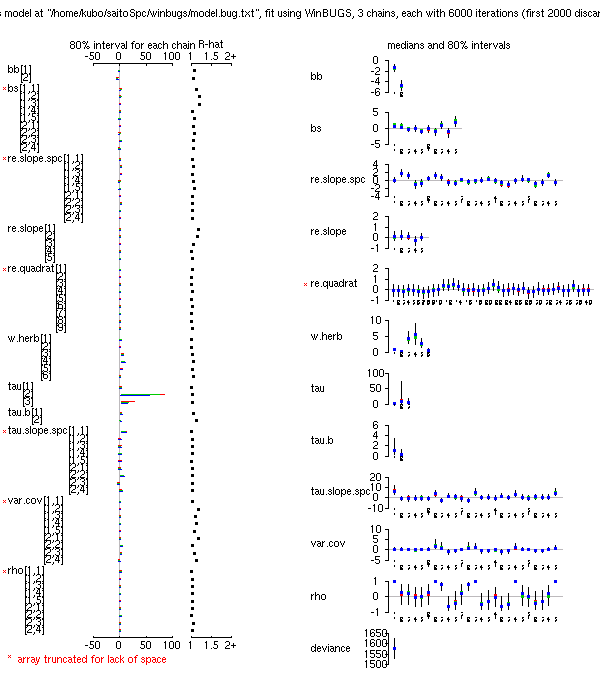
(事後分布表,
BUGS code).
-
改善のカギは
(ありていにいってわけのわからぬトコロもある)
「草本 6 種ごとに shading の強さ (加重)」
パラメーターのおきかたにある.
昨日までのモデルでは
for (quadrat in 1:N.quadrat) { # 蛇足ながら shading[] の計算はわりと無根拠
shading[quadrat] <- 1 - exp(-inprod(w.herb[], Herb[quadrat,]))
}
for (hspc in 1:N.herb) {
w.herb[hspc] <- exp(log.w.herb[hspc])
log.w.herb[hspc] ~ dnorm(0.0, tau[2])
}
というふうに
「加重」 w.herbp[]
の対数値である log.w.herb[]
がこのように設定されてた.
ヒトコトでいえば,
「ゼロを中心にして 6 種が好き勝手な値をとれ,
ただし全体のばらつき (分散) は 1 / tau[2]
と制約する」
といった階層ベイズモデル.
-
しかしながら,
ぢつはこれではまずくて
……
「草本全体 (全 6 種) による shading」
shading[quadrat]
にさらに樹木応答がわの係数がかけられて,
「樹木側の係数」 × shading[quadrat]
というカタチで線形予測子 (linear predictor)
にくみこまれていて,
ですね
……
このかけ算値全体の大小を決めてるのは樹木の係数のほうなのか,
それとも shading[] の平均値なのか,
MCMC 計算やってくれる WinBUGS にとってはわからーん,
という状況なんだよね.
-
そこで
「一般性を失うことなく」
(without losing generality)
もひとつ制約をくわえてやらねばならない.
これでいいのかどうか,
いまいち確信がもてない部分があるんだけど,
とりあえず書いておこう.
-
たとえば,
今回の策では BUGS code をこう書いてるわけで,
for (quadrat in 1:N.quadrat) {
shading[quadrat] <- 1 - exp(-inprod(w.herb[], Herb[quadrat,]))
}
w.herb[1] <- 1.0 # 第 1 種の値を強制的に 1 とおく
for (hspc in 2:N.herb) { # 第 2 種以降は好きなよーに
w.herb[hspc] <- exp(log.w.herb[hspc])
}
for (hspc in 1:N.herb) { # log.w.herb[1] は計算する意味がないけど
log.w.herb[hspc] ~ dnorm(0.0, tau[2])
}
つまり 6 種ある草本のうち一個の加重値
w.herb[]
を強制的に 1 においてしまう
(log.w.herb[] をゼロと設定すればいいんだけど,
諸般の事情とやらでめんどうなので放置している),
という方法だ.
ここでは第 1 の種の値を固定している.
第 2 の草本種以降の log.w.herb[] に関しては
(今回はたまたまうまくいっただけなのかもしれないが)
ゼロを中心とする事前分布を設定している.
-
この方式でマズいことになりそうなのは,
全草本の中で「基準」にえらんだ草本種
(ここでは第 1 の種)
が「めちゃくちゃかわりもの」であった場合だろうな
……
その場合でも計算は収束するはずだと思うんだけど,
なんというか推定値に偏りが生じてしまうだろうな.
-
だからといって第 2 種以降
log.w.herb[hspc] ~ dnorm(0.0, tau[2])
と設定してる事前分布の平均は 0.0 以外ありえないと思うんだけど
……
-
ともかく「なぜ収束が遅いのか (あるいはそもそもうまくいかないのか)?」
の原因は上の方法で確認できた,
ということ.
問題はよりよい対策だな.
パラメーター数を増やさずに何とかならないものかな?
-
まあ,
一番簡単には草本 5 種の加重値の事前分布を無情報事前分布
(non-informative prior)
にする,
というのは無難な解決策だ
……
無情報にしたらどうなることやら,
という懸念もあるけどね.
-
といったコトどもをうだうだと書いてるうちに,
全 7ヶ所の放棄スキー場をつかった計算
(上の計算ではヘンなスキー場 2ヶ所を除外している)
に 2900 秒を費やして終了した
……
うーむ,
やっぱり Site 6 は
……
ということで,
とうめん 5 スキー場でいくか?
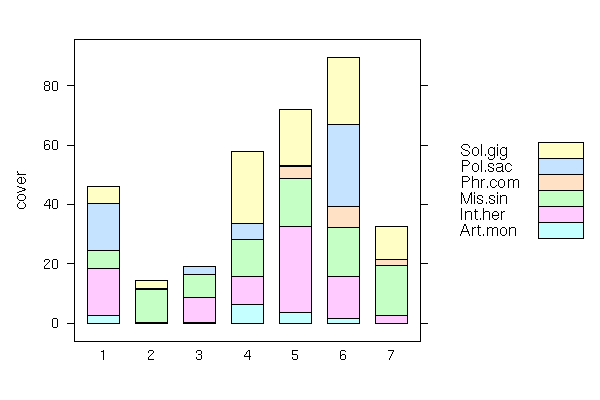
barchart(cover ~ as.factor(slope), groups = as.factor(herb), data = dd, stack = T,
auto.key = list(space = "right", rectangles = T, reverse.rows = TRUE))
-
昼飯.
しまった,
A801 院生部屋のプリンター LP-2000C の感光体ユニットの交換を忘れてた
……
-
1315 ごろから佐竹さんととある遺伝子発現モデリングの相談.
まあ,
いろいろわけのわからぬ測定誤差らしきモノがあるわけで
……
-
しかしその遺伝子の発現の挙動に関する実験室で得られた知見と,
いま手もとにある野外サンプリングデータの対応関係はわかったので,
半経験論的な階層ベイズモデルの構築は可能そうだ
……
いろいろ検討してみたんだけど,
少なくとも二つの latent state variable を考えればよさそう.
-
遺伝子発現モデリングの設計 (まだ実装はしてない)
は夕方ごろひとくぎりついたので,
午前中に中途半端なまま放置してたスキー場植生モデルの再検討.
-
草本の加重 shading 値の事前分布を無情報 (non-informative)
にしてみる.
いくつかの方式を試行錯誤してみると
……
これでうまくいってるように見える.
やはり
全 5 樹種 (放棄スキー場数 5)
で
6000 MCMC step (計算時間 1300 秒 ぐらい),
まあままの収束
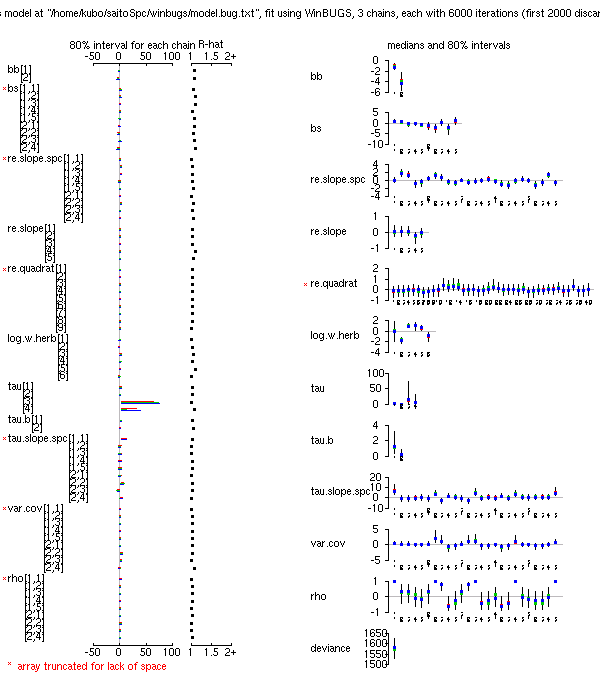
(事後分布表,
BUGS code).
-
……
これでいちゃもんつけられそうな点をひとつ減らすことができたな,
と斎藤君と相談.
まあこの観測データに関する統計モデリングはこんなところでしょう,
という方向で.
-
2010 研究室発.
2025 帰宅.
晩飯の準備.
晩飯.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0800):
ヨーグルト.
リンゴ.
- 昼 (1240):
研究室お茶部屋.
米麦 0.6 合.
キャベツ・タマネギ・ニンジン・ひき肉のトマト煮.
- 晩 (2120):
ピーマン・モヤシ・ネギ・卵の焼きそば.
コンブサラダ.