ぎょーむ日誌 2007-09-03

2007 年 09 月 03 日 (月)

• 0800 起床． 朝飯． コーヒー． 怠業 …… う， 今日から書類上の夏休みなんだけど， ホントに休んでしまった．
• 1220 自宅発． 曇． 1235 研究室着．
• 数セミ原稿の修正． あれこれ修正， ファイルアップロード， 数セミ編集部に連絡， で 1450 ひとまず終了．
• 昼飯． なぜか (プランクトンとはまた別の ECOAS データである) 雄阿寒岳樹木成長データの雑談， とか．
• ECOAS プランクトンデータの統計モデリングの検討． また占部さんからいろいろと教えていただいたのだが …… 窒素だのリンだのがどこにあるか， という観測値は
  • 何やらいろいろと相互作用のある動態モデルで 記述できる (がそのモデルの定式化されてない?)
  • 平衡状態にちかい値
  …… と考えられているみたいだねえ．
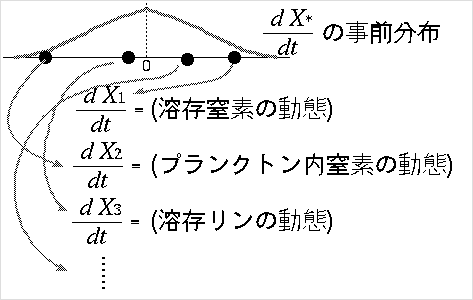
• ならば観測したヒトたちのアタマの中にあわせた 統計モデリング， ということになると …… たとえばこういうものになるのではないかな?

• 上の図が示してるモデル， ちょっとばかり新奇に見えるしろものだなぁ …… こういう陸水系の生物-無生物の C-H-P のボックスモデルって ありがちだとは思うんだけど， ここで系が平衡状態 (dX*/dt = 0) とは考えずに， 「変化量がどれもほぼゼロ」 (dX*/dt がゼロにちかい) と考えて， その変化量の分布が Gibbs 分布にしたがうと考えています， という …… まあ， 正しいのかどうか， 使いものになるのかどうか， よくわからぬ統計モデリングではあるな．
• 他にアイデアもないので， またメイル書いてみる．

・リン添加実験によって Chl-a が増加する

ということで (ECOAS data との対応: Chl-a と DTP, DIN を比較した場合，
DTP のほうが相関が高そうに見える)，やはり DTP と seston P は「全リン」
とはまとめずに，わけて考えたほうがよさそうな気がしてきました．

この場合，リン濃度は環境収容力というより，Chl-a 増加速度などを決めてい
るような気がします．平衡状態の現存量は系へのリンの出入りと seston に取
り込まれる速度と放出される速度のかねあいで決まりそうですね．

ということで，推定できるかどうかわかりませんが，何か動態モデルの平衡状
態を満たすようなパラメーターの値をデータから推定せよ，という問題のよう
な気がしてきました．

動物プランクトン・魚その他の影響はあとから考慮することにして，とりあえ
ず植物プランクトンとリンだけあるような系を考えます．DTP である PI と
seston P である PO の濃度は，たとえばと下のようなダイナミスが成立してい
るとします (このダイナミクスは正の平衡状態をもちます):

dPI/dt = r1 - r2 * PI - r3 * PI * PO + r4 * PO
dPO/dt = - r2 * PO + r3 * PO * PI - r4 * PO

r1 は系外からの PI の流入速度，
r2 は系から水が流出する速度で PI も PO もいっしょに流される，
r3 は DTP が seston P になる速度，
r4 は seston P が DTP になる速度，

といったかんじで，たとえば r1, ... , r4 のパラメーターが標高に依存した
り，植物プランクトンの増殖速度である r3 が標高だけでなく PI の増加関数
であればよいように思います (ちょっと現象論的ですが)．つまり r のたぐい
が環境要因の関数，たとえば r1 = exp(a + b * height) といった関数になっ
ている，とういことです．

このような式がずらずらと (実際には窒素や動物プランクトンなんかのダイナ
ミクスも列挙されるのでしょうが) あるとして，ここで系が平衡状態に近いと
仮定するわけです．

モデル屋なら dPI/dt = 0 とかおくのでしょうが，われわれは実際の観測デー
タを扱っているので，dPI/dt その他の変化率がゼロに近い，つまりゼロを中心
とする確率分布，たとえば平均ゼロで標準偏差σの正規分布にしたがうと仮定
します．

このダイナミクス全体を階層ベイズモデルとしてあつかうわけですが，
このときに「平衡状態からのずれのばらつき」σがどの式でも共通していて，
しかも尤度を高くするためにはこの値ができるだけ小さくなる方向に，r1,
..., r4 の値を決定するパラメーター (上の例だと a だの b だの) の事後分
布を計算すればよいでしょう．これは GLMM なんかの「個体差は平均ゼロで標
準偏差σの確率分布にしたがうようにする，ただし個体差のばらつきσは可能
なかぎり小さくする」といった考えかたと同じです．

結局のところ，r1, ..., r4 といったパラメーターが標高その他にどう依存す
るか，といった結果が得られるはずだと思います (MCMC 計算がうまく収束し
てくれれば)．

• 1850 研究室発． 1900 帰宅． 体重 68.6 kg． うんどう． 晩飯．
• [今日の運動]
  • エアロバイク 45 分間． 400kcal．
• [今日の食卓]
  • 朝 (1100): 米麦 0.6 合． マイタケ・卵の炒めもの． ネギ・豆腐の味噌汁．
  • 昼 (1430): 研究室お茶部屋． 米麦 0.6 合． インスタント味噌汁．
  • 晩 (2200): 米麦 0.8 合． サンマの塩焼． モヤシ・ネギ・豆腐の煮物． キュウリ． トウモロコシ．