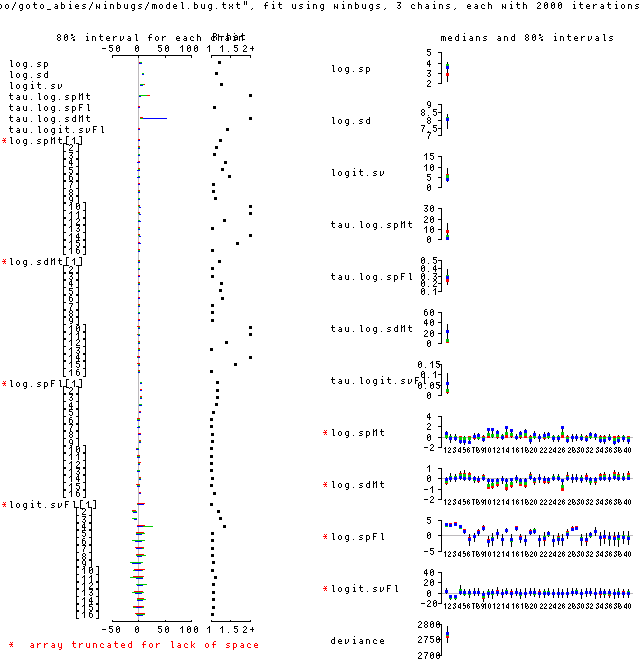
ぎょーむ日誌 2007-04-08
2007 年 04 月 08 日 (日)
-
0900 起床.
コーヒー.
朝飯.
ねむい.
怠業.
-
1300 自宅発.
昼飯.
北九条小学校で地方選挙の投票.
札幌駅周辺をふらふらしてから
1500 研究室着.
-
昨晩やらせておいた計算だが
……
なぜか 2400 秒で終わったのはよいとして,
計算結果はヘボいな.
というのもモデル改造部分が
だめだめ
だからだ
……
といったことなんかは,
結果を見るとよく理解できる.
-
今回はトドマツ子供全体を齢 -2-|-3- で実生・稚樹とわけていて,
その観測された個体数にモデル (「末端」はポアソン分布)
をあてはめている.
で,
「実生にくらべての稚樹の少なさ」
をなんとなく倒木に与える
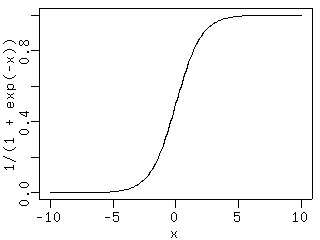
logit.sv*
系のパラメーターで説明しようとしたわけだが
……
やっぱ,
こういうわけかたでは数にそもそも差がでないので,
そういう結果になっているな.
つまり倒木間共通の logit.sv
が 5 とかそんな値だよね.
これって事実上の確率 1,
その意味するところは
「こういう分けかたを単純に『サイズクラス』とみなすのはまちがい」
ということだ.
-
で,
こういうとんでもない値をとるパラメーターは
確率 1 にちかいどうでもよい部分を乱暴にうろつきまわりやがるし,
「倒木差」パラメーターもでたらめに上下に移動するから,
他のパラメーターの収束も悪くなる,
と.
いやはや.
-
さーて,
このあたりどう料理してやろうかな
……
一番いいのは全部の齢構造をそのままあつかうことなんだけど,
これは数日前にすでに実験ずみで計算時間が絶望的に増大する,
と.
WinBUGS
のモデルを定義する BUGS 言語は
「ど貧の中のぎりぎりの工夫」
というかんじ & 「尤度をかくす」という興味ぶかものなんだけど,
たくさんの弱点があって
……
たとえば,
一変量確率分布からたくさんの事後分布を生成させるのは
死ぬほど時間かかる,
というのがここで直面していた問題だったのである.
-
データ構造全体をながめると,
このトドマツデータから推定しうる
``demographic parameter''
なるものはかなり制限されてるんだよねえ
……
-
めんどうなので,
毎年の生残確率
p はとりあえず一定とする.
すると一歳以上の条件つき齢分布は
pa - 1 (1 - p)
となる.
このときにある子供を選んだときに
実生クラス (a = 1, 2) である確率は
1 - p2
と計算されるし,
稚樹クラス (a > 2) である確率は
p2
になっちまう
……
という性質を使ってみるのはどうかしらん?
昨日のいいかげんな計算よりは多少はマシか?
-
まあ実際のところ生残確率
p
は一定ではあるまいよ
……
うんぬんといった一見もっともらしいギロンとやらは別にして,
だな
(このギロンは一見するほどにはもっともらしくない).
それ以前の問題として,
この
1 - p2
と
p2
に分割されるってハナシは本質的には昨日のだめだめ計算と
同じような気がしてきた.
けっきょく実生・稚樹が半々にになってオワるのでは?
-
……
いーや,
そうではないな.
この問題に関しては,
たとえば
1 - p2 < 0.5
とかになってもぜんぜん問題ないわけだ
(p > およそ0.7 でそうなる).
まあ,
観測されてる齢分布はこんなかんぢなんだけどね.
> summary(as.factor(maternity$age))
1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 18 22 23 27
73 138 87 27 23 24 8 10 1 2 3 3 2 2 4 3 1 1 1
-
こういうの見ると,
生残確率の齢・サイズ依存性や個体差を考えたくなるわけだが
……
まあ,
今回はそのへん無視して
(とゆーか,
かかる面倒どもはことごとく「倒木差」に罪をかぶせてしまう,
といういつもの
random effects
悪用わざにもちこんで)
モデリングしてみようか.
-
コードかきなおして,
1939 再計算を命じる.
-
1955 研究室発.
2015 帰宅.
晩飯.
-
[今日の運動]
-
腹筋運動 30 ×
3 回.
腕立ふせ 10 ×
3 回.
スクワット 100 回.
-
[今日の食卓]
- 朝 (0930):
ラスク.
- 昼 (1340):
北 16 西 3 のスープカレー屋 Maruhuku
で野菜カレー.
- 晩 (2140):
スパゲッティー.
タマネギ・ニンニクのトマトソース.