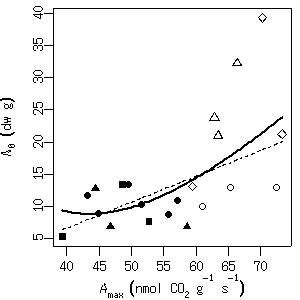
[光合成速度 vs 葉重量]
nlme()
に微分不可能な関数を計算させるのは面倒 (不可能?)
なので,
みょーな漸近線をもつ関数をでっちあげてみた.
そいつは selfStart() 関数として定義されねばならぬ.
さらにデータも面倒で,
ふつーの data.frame()
はダメで groupedData()
なるものを使わねばならぬ
(非線形関数などの場合).
library(nlme)
の使いかたの練習,
というか.
これ,
すごくややこしくなってますよ
(と思って
nlme 本
ながめてみたら,
じつは今に始まったことではなく昔からややこしいシロモノだった,
とわかった).

nlme()
に微分不可能な関数を計算させるのは面倒 (不可能?)
なので,
みょーな漸近線をもつ関数をでっちあげてみた.
そいつは selfStart() 関数として定義されねばならぬ.
さらにデータも面倒で,
ふつーの data.frame()
はダメで groupedData()
なるものを使わねばならぬ
(非線形関数などの場合).
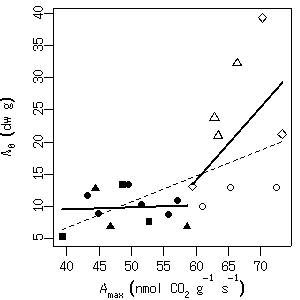
formula
じたいがまがりなりにも線形なので,
selfStart 関数つかわず推定計算できた.
この状況だと,
なぜかしら (互換性維持?)
random = a + b + c ~ 1 | plotといった古い
nlme() 書式も使えた.
で,
この二分割モデルは AIC 的にはさらに劣悪,
と.
こちらの 2 パラメーター線形混合モデルでは
サンプル場所によって切片・傾きが異なるとしているので,
上とはびみょーに異なった推定結果となっている.