ぎょーむ日誌 2006-06-07
2006 年 06 月 07 日 (水)
-
0700 起床.
朝飯.
コーヒー.
0835 自宅発.
曇.
0850 研究室着.
-
アタマが整理されてきたような気がするので,
アカマツ成長の MCMC 計算プログラムかきに着手してみる.
例の屋久島葉死亡モデルの計算中核部の改造.
なんと Perl+SWIG でかかれているこのコード,
階層ベイズモデルを計算するために
けっこうややこしい階層処理が入っていて
(当時はそうするしかないと考えていた),
このへんはたぶんいらないだろうからりすとら.
使える部品 (class)
を整理する.
-
で,
どんどん実装していくわけだが
……
コード書きなおしてるうちに,
いまさらながら
今回のモデリングに関して,
ひじょーにまぬけなしくじりに気づいた.
cohort2000 の成長が悪い,
ということと cohort1999 の成長がよろしくない,
というのは数式の上では識別がつかない!
つまり推定不可能だな.
-
しょうがないんでモデルを再検討.
-
……
にとりかかろうとしたところ,
塩寺さんの熱帯葉死亡モデリングのデータ解析こんさる.
うーむ,
Cox の比例ハザードモデルを
R
で推定計算しておられるんだけど,
「与えられた期間」
より長い base line hazzard 関数を計算できないのか
……
ということで,
coxph()
による推定はあきらめていただき,
survreg()
でワイブルな死亡曲線とかを使ってもらうことに.
-
アカマツ検討にもどる.
どうも茎直径分布を考えるハナシはダメそうだな
……
ということで,
パイプモデル系の前提にもとづくモデリングはやめてみる.
-
枝さきにおける重量分配モデル,
みたいなのを考え,
いわば「欠測」データに該当するのが成長前の
cohort1999 の大きさ,
と考える.
cohort1999 の 2000 における成長,
そして cohort1999 と cohort2000 における資源分割を考えて,
と.
-
で,
ここで
(欠測をうめるための)
私のおきにいりアイデアである resampling はあきらめて,
なにかパラメトリックな事前分布におきかえてしまおう.
ここで興味ぶかいのは,
この欠測をうめるための事前分布は全個体共通としてよいところだ.
なぜかといえば,
「成長の遅さ」の個体差と
「初期状態の貧弱さ」の個体差は識別できないからである.
つまり今度はさきほどの識別不可能性を逆に悪用してやろう,
と.
-
さてさて,
問題がここまでさらに単純化されてしまったら
(というか resampling をあきらめたので)
JAGS
とかでもさらさらと
MCMC 計算できてしまうモデルが構築されつつあるような気がする.
とりあえず昼飯.
-
Perl 版の自作 MCMC 計算プログラムの改善はとりあえず中断.
JAGS 初めての実戦投入へのシークエンスを開始する.
まず JAGS のコードを読んで BUGS 文法の研究.
R とみかけが似ているわけだが
……
文末に
; がいるのかいらんのかよくわからん
(無くてもいちおう動作する,
とわかった).
-
よしやってみるか,
とコード書いてみる.
ついでに架空データも.
30 分もかからずにひととーりできた.
けど,
いきなり syntax error ではじきかえされる
……
~
と
<-
の使いわけに注意.
下のごとくでとりあえずは動く.
model {
for (i in 1:n.tree) {
bi[i] ~ dnorm(0, iv.bi);
y[i] ~ dnorm(
exp(b0 + bt * treatment[i] + bi[i] + x[i]),
iv.g
);
z[i] ~ dnorm(
exp(a0 + at * treatment[i]) * (y[i] - exp(x[i])),
iv.a
);
}
b0 ~ dnorm(0, 1.0e-6);
bt ~ dnorm(0, 1.0e-6);
a0 ~ dnorm(0, 1.0e-6);
at ~ dnorm(0, 1.0e-6);
iv.bi ~ dgamma(1.0e-3, 1.0e-3);
iv.x ~ dgamma(1.0e-3, 1.0e-3);
iv.g ~ dgamma(1.0e-3, 1.0e-3);
iv.a ~ dgamma(1.0e-3, 1.0e-3);
}
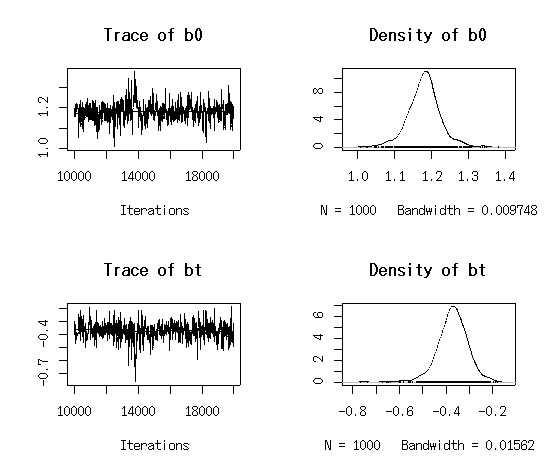
架空データつかった JAGS の MCMC 計算試運転
……
あっさりできた.
burn-in 10000 step の sampling 10000 step
で計算時間 15 秒
(PentiumM 1.6GHz).
作図は
RjpWiki の説明
とかが役にたつ.
架空データに設定しておいたとーりのパラメーター事後分布がでたな
……
なかなかすばらしい.
-
さて,
あとはこいつに本ものデータをどう食わせるか,
どういう推定結果になってしまうのか,
というあたりだが
……
ちょいひと休み.
-
しかし,
この JAGS の Gibbs sampler むちゃくちゃ速いなあ
……
まあ,
この架空データは実データにあわせて個体数 8
という状況なんだけど.
私が rejection sampling の関数とか書いたら,
すごく遅くなりそうな気がするんですが.
-
さて,
実データを JAGS 用データファイルを作るには,
R をもちいる.
JAGS はそのように設計されているんで.
R でデータを読みこみ,
必要な部分をぬきとり,
dump()
をつかって JAGS 用データファイルを作る.
たとえば,
こういうかんぢになる.
"n.tree" <-
as.integer(8)
"treatment" <-
c(1, 1, 1, 1, 0, 0, 0, 0)
"mx" <-
c(2.16615384615385, 2.32212389380531, 2.83478260869565, 5.38701298701299,
2.96280991735537, 5.14838709677419, 3.2787610619469, 5.78448275862069
)
"y" <-
c(28.2, 15.2, 31.8, 37.2, 26.1, 22.9, 21.5, 25.1)
"z" <-
c(17.6, 16.4, 16.3, 24.4, 23.9, 22.8, 24.7, 30.5)
-
で,
2000 ごろまでかかってべいづなモデリングの
工夫・試行錯誤・悪戦苦闘・七転八倒
……
JAGS が使えてよかった.
自作の Perl 版 Metropolis-Hastings sampler でやってたら,
おそらくさらにきちがいじみた状況を楽しまねばならぬところであった.
-
けっきょく「欠測」部分の事前分布をどうしたらよろしかろう,
というのが面倒の焦点であった.
resampling まではいかなかったけど
……
全個体共通の prior というアイデアはぜんぜんダメであった.
今晩得られた最良のモデルは,
(やや不本意なものがあるんだが)
事前分布を個体ごとに準備し,
その平均値を cohort2000 で決めてやる
……
まあ,
いったん放棄した
resampling アイデアの一部を流用してるわけで.
-
そして cohort1999 に関する処理の影響は「原理的に」
(とでもいうべきか)
依然として推定計算できない.
にもかかわらず
(なぜ cancel out できるのか説明するのが面倒なので)
それを含めたまま計算させている
……
まあ,
いづれにせよあってもなくてもよいパラメーターなんだけど.
-
それに対して,
いちばん先端部の cohort2000 への資源分配については
(個体差その他を考慮してなお)
明らかに減っているといえる
……
なんとか
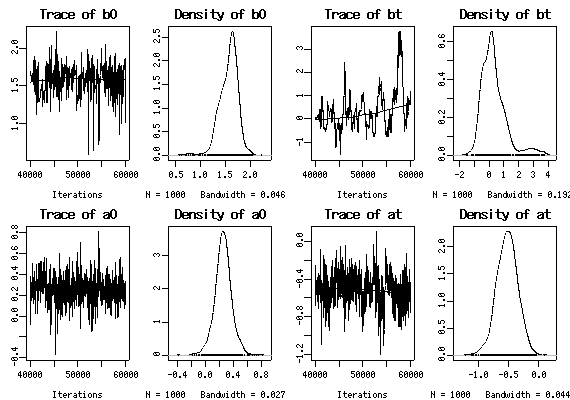
「使いものになる」結果が得られたところで本日は終了.
ちょっと無理矢理な部分もあるんだけど.
model {
b0 ~ dnorm(0, 1.0e-1);
bt ~ dnorm(0, 1.0e-1);
a0 ~ dnorm(0, 1.0e-1);
at ~ dnorm(0, 1.0e-1);
iv.x ~ dgamma(1.0e-1, 1.0e-3);
iv.g ~ dgamma(1.0e-3, 1.0e-3);
iv.a ~ dgamma(1.0e-3, 1.0e-3);
for (i in 1:n.tree) {
x[i] ~ dnorm(
mx[i] * exp(-(at + bt) * treatment[i]),
iv.x
)
y[i] ~ dnorm(
exp(b0 + bt * treatment[i]) * x[i],
iv.g
);
z[i] ~ dnorm(
exp(a0 + at * treatment[i]) * (y[i] - x[i]),
iv.a
);
}
}
------------------------------------------------------------------------
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
b0 1.5707 0.186 0.00587 0.01693
bt 0.3129 0.857 0.02709 0.11263
a0 0.2603 0.124 0.00391 0.00788
at -0.5195 0.173 0.00546 0.01491
x[1] 4.7551 2.801 0.08856 0.35565
x[2] 3.0440 1.914 0.06052 0.23131
x[3] 5.6167 3.294 0.10416 0.41052
x[4] 7.5072 4.469 0.14133 0.58324
x[5] 4.6935 1.564 0.04946 0.16381
x[6] 4.9561 0.930 0.02940 0.09669
x[7] 4.0829 0.977 0.03090 0.09581
x[8] 5.4080 0.923 0.02918 0.09687
iv.x 68.4803 279.713 8.84529 17.38780
iv.g 65.0620 249.301 7.88358 13.45898
iv.a 0.0832 0.572 0.01810 0.02830
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
b0 1.20958 1.4580 1.603 1.6914 1.861
bt -0.78595 -0.2827 0.167 0.6841 2.914
a0 0.00788 0.1910 0.260 0.3308 0.512
at -0.87161 -0.6331 -0.517 -0.4075 -0.187
x[1] 0.24130 2.7066 4.458 6.1832 11.481
x[2] 0.22400 1.6915 2.667 4.3029 6.661
x[3] 0.31323 3.2326 5.214 7.5022 13.006
x[4] 0.48048 4.3256 6.666 10.5067 15.893
x[5] 2.75829 3.1660 4.726 5.5114 7.423
x[6] 3.54275 4.3730 4.994 5.2866 6.750
x[7] 2.77661 3.3414 3.926 4.6285 6.007
x[8] 3.81784 4.7601 5.506 5.8456 6.987
iv.x 0.06327 0.2717 0.597 3.8881 791.402
iv.g 0.00583 0.0205 0.293 15.5221 670.739
iv.a 0.00985 0.0309 0.047 0.0717 0.147
------------------------------------------------------------------------
私のぎょーむ時間を日々監視してるらしい院生たちから
久保さんもたまには日没後も仕事やってるんですね,
といった勤務評価うけつつ
2015 研究室発.
2035 帰宅.
晩飯の準備.
運動.
体重 73.2kg.
晩飯.
[今日の運動]
[今日の食卓]
- 朝 (0730):
米麦 0.6 合.
ネギ・ブナシメジ・コンニャク・鶏ササミの煮物.
- 昼 (1340):
研究室お茶部屋.
米麦 0.6 合.
ネギ・ブナシメジ・コンニャク・鶏ササミの煮物.
- 晩 (2240):
米麦 1.0 合.
タマネギ・ジャガイモ・豆腐のカレー.


