- McCullagh, P. and Nelder, J.A. 1989. Generalized linear model. Chapman and Hill.
- Venables, W.N. and Ripley, B.D. 2002. Modern applied statistics with S (いわゆる MASS 本). Springer.
McCullagh and Nelder (1989, pp. 125-6) prefer a variation
of this model, in which the
n
data points are assumed to have been sampled from
k
clusters, and there is independent binomial sampling within
the clusters (whose size now varies with
n),
but the clusters have probabilities drawn independently from
a distribuiton of the same form as before.
Then it is easy to show that
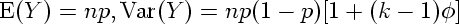
This does provide an explanation for the
ad hoc
adjustment model for variable
n,
but the assumption of the same number of (equally-sized)
clusters for each observation seems rather artificial to us.
φ
ってのは (なにかできゴトの) 生起確率
p
が上述の cluster ごとにばらついるので，
その分散が
n p(1 - p)
ではなく上の variance 定義のごとく (cluster 間の差が入って)
でかくなってる，
というハナシが (引用箇所より) 上のほうに書いてある．
と
を定義して
(これは指数関数族の一般的な分布の scaling parameter になっている)，
問題の「F 検定でいいぢゃん」
なところ．
Asymptotic theory for this model suggests
(McCullagh and Nelder, 1989)
that changes in deviance and resisdual deviances scaled
by
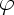have asymptotic chi-squared distributions with the appropriate
degrees of freedom. Since
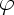must be estimated, this suggests that
F
tests are used in place of chi-squared tests in,
for example, the analysis of deviance and
addterm and dropterm.
At the level of the asymptotics there is no difference
between the use of estmators (7.7) and (7.8),
but we have seen that (7.8) has much less bias,
and it is this that is used by
anova.glm and addterm
and dropterm.
……
ほら，
どうです，
原文だってちょっとイカれてますよね?
……
どうでもいいんだけど，
推定量 (7.8) ってのは
の推定量 (もーめんと推定量ぢゃん?) で
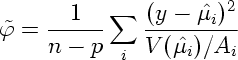
となるそーです． n - p は標本数 - パラメーター数で自由度だとか， V(μ) はその分布のなちゅらるな分散関数だと．
が 1 である (overdispersion なし)
として計算してるわけだけど，
これが 1 でなけりゃー overdispersion でも
underdispersion でもいいよね，
というようなことを考えようとしている，
と．
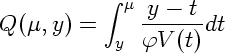
となる quasi likelihood を提案した， と (これを最大化するのが quasi likelihood estimation)． これって出自からして確率分布とかそういうふつーの統計学からは 完全に逸脱しちゃってるくせに， バターに対するマーガリン的な偽物 (ニセ対数尤度) になってるわけで．
として上の積分を計算するとあーら不思議
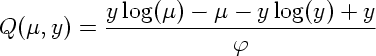
となるわけだが， これはポアソン分布の対数尤度
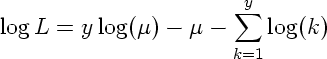
になんだか似てるじゃありませんか …… とゆーか， 上記オカしいヒトたちはそうなるように quasi likelihood を定義していたってこと．
が 1 なら qusi likelihood 最大化と
対数尤度最大化は同じ
μ
によってなされるよね
(
y
は定数だから)．
が 1 ぢゃないとき
(つまり overdispersion や underdispersion あるとき)
でさえ，
求めたいパラメーター
μ
の推定値は quasi だろーがそうぢゃなかろーが常に同じなのである．
これは他ならぬ
を
μ
とは別個にというか「あとづけ」で
(上の推定量 (7.8) とやらをもちいて)
計算しちゃうためである．
つまり
μ
の推定値を計算するときは，
あたかも
が定数であるかのようにして扱われてしまう，
と．
- (μ みたいな) パラメーターの推定値は同じ
-
しかし quasi のほうには
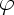があって，
これの大小で
「あてはまりの良さ」
(あるいはその「差」)
が変化する
> 1
つまり overdispersion のときはポアソン分布から逸脱して，
Q
の分子の絶対値が大きくなるんだけど分母も大きいくなってそれを
「補正」してる，
というような状況かな．
逆に
< 1
つまり underdispersion のときは
Q
の分子・分母がともに小さくなる，
と．
と定義されるそーで．
これで MASS 本引用の
``scaled by
''
とやらはわかった．
で，
消しちゃったらもうまったく対数尤度 (のパラメーター依存部分)
と同じぢゃん，
と思えてしまうわけですが
……
- 自由度だのばらつきパラメーターで「すけいりんぐ」 した quasi deviance は chi-squared 分布に漸近する
- F 分布は (chi-squared 乱数) / (chi-squared 乱数) の分布である
で分散を強めてみたポアソン分布って何さー!!」
と絶叫しても，
宇宙のどこからも答えは帰ってこないのである
……
蛇足ながら，
ポアソン分布の平均値にばらつきあると仮定してる
(ばらつきはガンマ分布)
のが「負の二項分布」で
R
では glm.nb()
による推定計算が安直である
(quasi いらん)．
- 北大構内走 35 分間．
- 朝 (0740): 米麦 0.8 合． ニンジン・タマネギ・セロリ・豆腐のカレー．
- 昼 (1350): 研究室お茶部屋． 米麦 0.5 合． ニンジン・タマネギ・セロリ・豆腐のカレー．
- 晩 (2230): 米麦 0.8 合． ネギ・ニンニク・イカの炒めもの． 乾燥野菜海藻スープ．